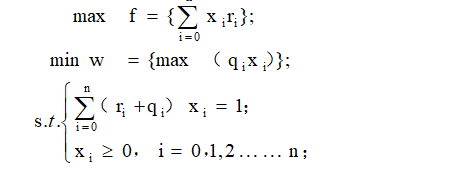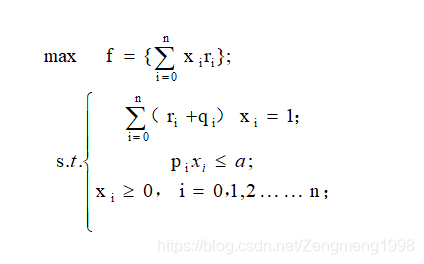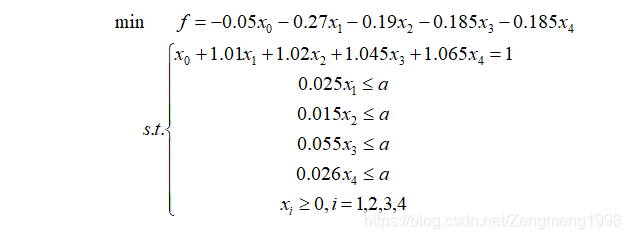不难看出这是一道典型的组合优化题,根据题意,客户希望冒着最小的风险得到最大的收益,想要做这一点,就需要数学的帮助了。同时,问题1与问题2的求解模型是一样的,那么在给出模型的求解方案后,也需要有敏锐的观察力来分析出一些弦外之声,这可能需要结合当时的政策去做一些恰当的分析了(大胆yy)。
针对问题2,可得到单目标规划公式:

这里求解方式与问题1相同,笔者不做赘述,根据问题的所给的投资资产数据,
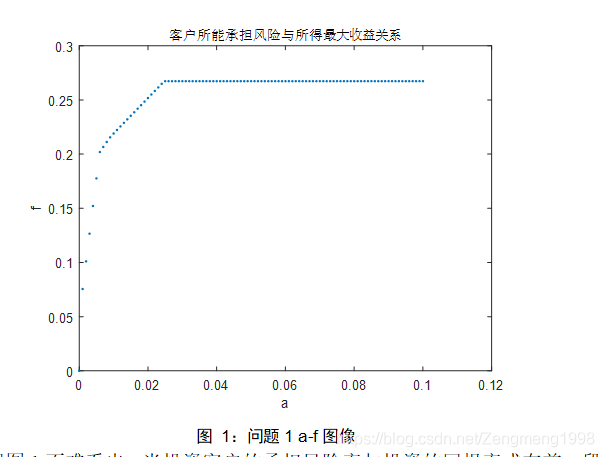
得到如图2所示的与f的关系图像。
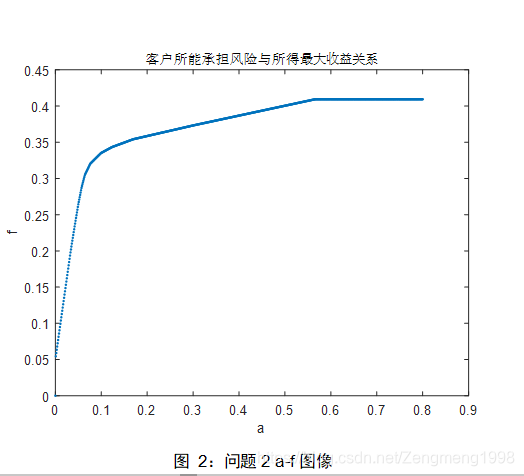
根据图2,我们可以得到f关于的变化规律,当客户的可承担风险率接近或大于60%时,可以得到的最大的回报,因此笔者取=0.6,代入模型中通过matlab求解得到:
y=(0.0000,0.0000,0.0000,0.9434,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000);
f =0.4094;
本文主要内容为建模过程的硬核求解部分,其余分析内容,笔者做出省略,请读者自行大胆yy,模型建立求解的过程的不足之处,望读者多加指正。其中代码笔者将分享至账号CSDN主页的资源与Github中,有进一步研究需求的读者可自行移步下载。
[1]数模课程ppt
[2]陈云贤,证券投资论,北京工业大学出版社,北京,1992.
[3]程仕军,系统工程,极大化证券投资组合的投资收益率,1994.
Python
数学
建
模
线性规划
投资
收益与风险
模
型
模
型 I : 固定风险水平, 优化收益
模
型 II : 固定盈利水平, 极小化风险
模
型 III : 两个目标函数加权求和
市场上有 nnn 种资产 si{s_i}si ( i=1,2,⋯ ,ni = 1,2, \cdots ,ni=1,2,⋯,n )可以选择,现用数额为 MMM 的充分大的资金作一个时期的
投资
。这 nnn 种资产在这一时期内购买 si{s_i}si 的平均收益率为 ri{r_i}ri ,风险损失率为 qi{q_i}qi ,
投资
越分散
(数
模
)
投资
证券:
题目:某银行经理计划用一笔资金进行有价证券
投资
,可共购进的证券以及其信用等级,到期年限,到期税前收益如下表。按照规定,市证卷的收益可以免税,其他证卷得到收益按50%的税率纳税,此外还有以下限制:
(1)政府及代办机构的证券总共至少要购进400万元;
(2)所购证券的平均信用等级不超过1.4(信用等级越小,信用程度越高)
(3)所购证券的平均到期年限不超过5年
问(1)若该经理由1000万元资金,应如何
投资
?
(2)如果能够以2.75%的利率借到不超过100万元资金,该经理应如何操作?
for (k = 2; k <= m; ++k) {// 从第二个阶段到最后一个阶段
for (i = 0; i <= n; ++i) { // 遍历所有的
投资
金额
t[i] = f[i];// 第k阶段初始最优解 认为是把所有金额投给第k个项目
cin >&...
m 元钱,n项
投资
, fi (x): 将 x 元投入第 i 个项目的效益. 求使得总效益最大的
投资
方案。
这个
问题
是一个优化
问题
,我们要找到一种
投资
方案(
组合
方式),这种方案就是你可以把一个钱拆开,所有的钱都是整数,把钱拆开成若干份,每一份都是大于等于0,并且是整数范围内的,所有的前的总数是不变的,所以所有的总数约束条件不变,总数不变的前提下,如何把钱分配的更加合理
三、
建
模
问题
的解是向量 < x1, x2, …, xn >, xi 是投给项目i 的钱数,i =1,
本题选自1998年全国大学生
数学
建
模
竞赛A题
例:市场上有种资产(如股票、债券、……)si(i=1,2,...,n)供
投资
者选择,某公司有数额为M的一笔相当大的资金可用作一个时期的
投资
。公司财务分析人员对这n种资产进行了评估,估算出在这一时期内购买资产si的平均收益率为ri,并预测出购买si的风险损失率为qi。考虑到
投资
越分散,总的风险越小,公司确定,当用这笔资金购买若干种资产时,总体风险可用所
投资
的si中最大的一个风险来度量。
购买si要付交易费,费率为pi,并且当购买额不超过给定ui时,交易费按购买
A题
投资
的收益和风险
市场上有n种资产(如股票、债券、…)Si ( i=1,…n) 供
投资
者选择,某公司有数额为M的一笔相当大的资金可用作一个时期的
投资
。公司财务分析人员对这n种资产进行
了评估,估算出在这一时期内购买Si的平均收益率为ri,并预测出购买Si的风险损失率为qi。考虑到
投资
越分散,总的风险越小,公司确定,当用这笔资金购买若干种资产时,总体风险可用所
投资
的Si中最大的一个风险来度量。
购买Si要付交易费,费率为pi,并且当购买额不超过给定值ui时,交易费按购买ui计算(不买当然无须付费)。另外,假定同期银行存款利率是ro, 且既无交易费又无风险。(ro=5%)
minmax
数学
建
模
是一种优化方法,它旨在寻找一个决策变量的最佳取值,以最小化或最大化一个目标函数。这种
建
模
方法通常用于解决决策
问题
,例如制定最佳
投资
组合
、资源分配、路径规划等。
在minmax
建
模
中,我们首先定义一个目标函数,希望将其最小化或最大化。然后,我们确定一组约束条件,以限制决策变量的取值范围或相关关系。接下来,我们将
问题
转化为一个
数学
表达式,通过对决策变量和目标函数进行合理的
数学
操作来达到最优解。
minmax
模
型的一种常见形式是线性规划
问题
。在线性规划中,目标函数和约束条件都是线性的,通过线性规划算法可以高效地求解最优解。另一种形式是非线性规划
问题
,其中目标函数或者约束条件中包含非线性关系,需要使用更复杂的算法来求解。
minmax
数学
建
模
的优点是可以将实际
问题
转化为
数学
问题
,并确定一个全局最优解。它在实际应用中具有广泛的适用性,可以解决各种决策
问题
。然而,minmax
建
模
也有一些局限性,例如可能存在多个最优解或者求解复杂度较高。
总之,minmax
数学
建
模
是一种重要的优化方法,通过将实际
问题
转化为
数学
问题
,并使用相应求解算法,可以寻找到一个决策变量的最佳取值,从而优化目标函数的结果。它在决策
问题
中具有广泛的应用,并为我们提供了一种有效的
问题
求解思路。