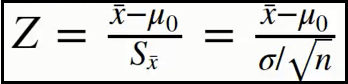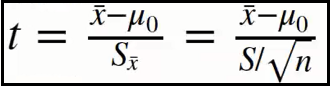推断统计：参数估计和假设检验_数据分析与统计学之美的博客-CSDN ...

1、总体、个体、样本和样本容量

1）总体、个体、样本和样本容量的概念

总体：我们所要研究的问题的所有数据，称为总体。
个体：总体中的某个数据，就是个体。总体是所有个体构成的集合。
样本：从总体中抽取的部分个体，就构成了一个样本。样本是总体的一个子集。
样本容量：样本中包含的个体数量，称为样本容量。
2）本文章使用的相关python库

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
from sklearn.datasets import load_iris
from scipy import stats
sns.set(style="darkgrid")
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore")
2、推断统计的概念
 
1）推断统计的概念
 
  “推断统计”研究的是用样本数据去推断总体数量特征的一种方法。它是在对样本数据进行描述的基础上，对统计总体的未知数量特征做出以概率形式表述的推断。 
2）为什么要进行推断统计？
 
  在实际研究中，总体数据的获取往往是比较困难的，总体参数一般也是未知的。因此，我们就需要利用总体的某个样本，通过样本统计量去估计总体参数。基于这个需求，我们就需要学习推断统计。
   通过上述叙述，我们给推断统计做一个说明。“推断统计”就是利用样本统计量，去推断总体参数的一种方法。
    
3、参数估计(点估计和区间估计)
 
1）参数估计、点估计和区间统计的概念
 
参数估计：用样本统计量去估计总体的参数。比如，用样本均值去估计总体均值，用样本方差去估计总体方差。
点估计：用样本统计量的某个取值，直接作为总体参数的估计值。
区间估计：在点估计的基础之上，给出总体参数估计值的一个区间范围，该区间通常由样本统计量加减估计误差得到。 
2）点估计说明
 
① 怎么求鸢尾花的平均花瓣长度？
 
  事实上，世界上鸢尾花千千万，我们总不能说把所有的鸢尾花的数据信息，都统计出来。因此，这就需要我们用样本均值去估计总体均值。 
iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))
# 计算鸢尾花花瓣长度的均值
df["petal length (cm)"].mean()
结果如下：
 
 结果分析：点估计有点简单粗暴，容易受到随机抽样的影响，很难保证结果的准确性。但是，点估计也不是一无是处，样本值是来自总体的一个抽样，在一定程度上还是可以反映出总体的一部分特征。同时，样本容量越接近总体容量，点估计值也会越准确。
    
3）区间估计说明
 
① 什么是区间估计？
 
  当你碰到一个陌生人，我让你判断出这个人的年龄是多少？这里有两种方式完成你的推断。第一，这个人25岁。第二，这个人20-25岁之间。哪种结果更让你信服呢？很明显第二种更让人信服。对于第一种说法，相当于上述的点估计。第二种，相当于区间估计，就是给定一个区间，这个区间包含真值。
   统计学中对区间估计的定义：在点估计的基础之上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。 
② 问题：获取一个抽样样本后，如何确定置信区间和置信度？
 
要确定置信区间和置信度，就需要知道样本和总体，在分布上有怎样的联系。中心极限定理给出了这个问题很好的回答。上述疑问将在下面为您一一揭晓。
    
4、中心极限定理
 
1）中心极限定理的概念
 
  设从均值为μ，方差为σ²的任意一个总体中，抽取样本量为n的样本。当n充分大的时候，样本均值X拔近似服从均值为μ，方差为σ²/n的正态分布。
 
 注意：中心极限定理要求n充分大，但是多大才叫充分大呢？一般在统计学中n>=30称之为大样本(统计学中的一种经验说法)。因此在实际生产中，不用多想，肯定都是大样本。 
2）中心极限定理的推导(手写推导)
 
  设X1,X1,…,Xn是从总体中抽取出来的样本容量为n的随机样本，假设总体均值为μ，方差为σ²。那么很显然这n个样本是独立同分布的，“独立”指的就是每个个体被抽到的概率是相同的，每个球被抽到也不会影响其它球被抽到，“同分布”指的是每一个个体都和总体分布一样，均值为μ，方差为σ²。
   基于上述叙述，下面我们来推导样本均值X拔的分布。
  
3）由中心极限定理得出的几个结论
 
不管进行多少次抽样，每次抽样都会得到一个均值。当每次抽取的样本容量n足够大时，样本均值总会围绕总体均值附近，呈现正态分布。
当样本容量n足够大时，样本均值构成正态分布，样本均值近似等于总体均值μ，而样本方差等于总体方差σ²除以n，即σ²/n。
样本均值分布的标准差，我们称之为标准误差，简称“标准误”。 
4）python实现中心极限定理
 
# 设置一个随机种子，保证每次产生的随机数都是一定的
np.random.seed(3)
# 产生均值为50，标准差为80，大小为100000的一个总体
all_ = np.random.normal(loc=50,scale=80,size=100000)
# 创建一个样本均值数组
mean_array = np.zeros(10000)
for i in range(len(mean_array)):
    mean_array[i] = np.random.choice(all_,size=64,replace=True).mean()
display("样本的均值：",mean_array.mean())
display("样本的标准差：",mean_array.std())
display("偏度：",pd.Series(mean_array).skew())
sns.distplot(mean_array)
结果如下：
 
 从图中可以看出：样本均值近似等于总体均值50，而样本方差等于总体方差80除以8，即10。 
5、参数估计中置信区间的推导
 
  我们要知道什么是α值，什么是置信度，什么是置信区间，以及怎么求置信区间。首先要了解以下几方面的知识，才能有一个比较透彻的了解。 
1）什么是小概率事件？
2）随机变量的分布的概念。
3）标准正态分布的概率密度函数和和分布函数
4）随机变量的α分位数的概念。
5）标准正态的分位数表怎么得到的呢？
6）区间估计的概念。
7）置信水平1-α的解释
8）枢轴法求置信区间的步骤。 
1）什么是小概率事件？
 
“小概率事件”指的就是在一次随机试验中，几乎不可能发生。
假定参数是射击靶上10环的位置，随机进行一次射击，打在靶心10环的位置上的可能性很小，但是打中靶子的可能性确很大。然后用打在靶上的这个点画出一个区间，这个区间包含靶心的可能性就很大，这就是区间估计的基本思想。 
2）随机变量的分布的概念
 
3）标准正态分布的概率密度函数和和分布函数
 
4）随机变量的α分位数的概念
 
5）标准正态的分位数表怎么得到的呢？
 
① 标准正态分位数表的公式推导
 

 注意：红色方框中的公式，就是标准正态分布分位数表的由来。 
② 标准正态分布分位数表
 
6）区间估计的定义
 
7）置信水平1-α的解释
 
  对总体样本进行反复抽样(每次抽取到的样本容量都为n)，那么每个样本均值都会确定一个区间(a,b)，每个这样的区间要么包含总体参数，要么不包含总体参数，不能说成“以多大的概率包含总体的参数”。其中包含总体参数的区间有1-α个，而只有α个区间不包含总体参数，如下图所示(红色表示该样本构成的区间估计不包含总体参数，白色表示该样本构成的区间估计包含总体参数)。
   用一个详细的案例说明：如果对总体返回抽样10000次，每次抽样的样本量都是n，每个样本都会得到一个区间估计，那么10000次抽样，就会得到10000个区间。当置信水平1-α=95%时，那么就表示10000个区间中包含总体参数的有9500个抽样样本，只有500个样本不包含总体参数，这个不包含总体参数的样本就相当于我们估计错误。这个概率只有5%。这个5%在统计学中，就叫做小概率事件，也就是说在一次随机试验中，这个小概率事件不可能发生。
   即：当我们随机抽取一个样本容量为n的抽样样本，并且利用这个样本构造总体参数的置信区间，当指定了置信水平1-α=95%时，那么这个样本，基本就可以认为是包含了总体参数，也就是说，总体参数就在这个置信区间内。
  
8）枢轴法求置信区间的步骤(手写推导)
 
① 什么是枢轴量？
 
枢轴量指的就是包含待估计参数，而不包含其它未知参数，并且分布已知的一个量。
枢轴量设计到三个重要点：1、包含估计参数。2、不包含其它未知参数。3、该枢轴量的分布已知。 
②以总体μ的置信区间为例(方差σ²已知)，讲述枢轴量求置信区间的步骤。
 
6、假设检验
 
1）假设检验的概念
 
  假设检验，也称为显著性检验，指通过样本的统计量，来判断与总体参数之间是否存在差异(差异是否显著)。我们事先对总体参数进行一定的假设，然后通过收集到的数据，来验证我们之前作出的假设(总体参数)是否合理。
   在假设检验中，我们会建立两个完全对立的假设，分别为原假设H0与备择假设H1。然后根据样本信息进行分析判断，是选择接受原假设，还是拒绝原假设(接受备择假设)。假设检验基于“反证法”。首先，我们会假设原假设为真，如果在此基础上，得出了违反逻辑与常理的结论，则表明原假设是错误的，我们就接受备择假设。否则，我们就没有充分的理由推翻原假设，此时我们选择去接受原假设。 
2）假设检验的理论依据(小概率事件)
 
  在假设检验中，违反逻辑与常规的结论，就是小概奉事件。我们认为，小概率事件在一次试验中是不会发生的。我们首先认为原假设为真，如果在此基础上，小概率事件发生，则我们就拒绝原假设，否则，我们就选择去接受原假设。
   假设检验遵循“疑罪从无”的原则，接受原假设，并不代表原假设一定是正确的，只是我们没有充分的证据，去证明原假设是错误的，因此只能维持原假设。那么，假设检验中的小概率事件是怎么得出的呢？想想之前讲到的置信区间，是不是一切都验然开朗了？
   “疑罪从无”很形象的说明的假设检验向我们传达的含义。也就是说，当我们没有充分的理由拒绝原假设，就必须接受原假设，即使原假设是错误的，但是你找不到证据证明原假设是错误的，你就只能认为原假设是对的。反之，经过一次随机试验，你如果找到了某个理由拒绝了原假设，那么原假设肯定就是错误的，这个是一定的。 
3）P-Value值与显著性水平
 
  假设检验，用来检验样本的统计量与总体参数，是否存在显著性差异。那么如何才算显著呢？我们就可以计算一个概率值(P-Value)，该概率值可以认为就是支持原假设的概率，因为在假设检验中，通常原假设为等值假设，因此，P-Value也就表示样本统计量与总体参数无差异的概率。然后，我们再设定一个阈值，这个阈值叫做“显著性水平 ” (使用α表示)，通常α的取值为0.05(1-α叫做置信度)。当P-Value的值大于α时，接受原假设。当P-Value的值小于α时，拒绝原假设。简单记为：p值越小越拒绝原假设。软件中一般都会展示这个p值，那里的p值，指的就是我们这里所叙述的p值。
   假设检验和参数估计是推断统计的两个组成部分，都是利用样本对总体进行某种推断，但是两者进行推断的角度不同。参数估计讨论的是用样本统计量估计总体参数的一种方法，总体参数在估计前是未知的。而假设检验，则是对总体参数先提出一个假设，然后用样本信息去检验这个假设是否成立。 
4）假设检验的步骤
 
① 根据实际问题的要求，提出原假设和备择假设。
② 给出显著性水平α以及样本容量n。
③ 确定检验统计量和拒绝域。
④ 计算出检验统计量的值，并作出决策。 
5）单边检验和双边检验
 
6）常用的假设检验
 
① 单个正态总体均值的假设检验法(Z检验：方差已知)
 
  Z检验用来判断样本均值是否与总体均值具有显著性差异。Z检验是通过正态分布的理论来推断差异发生的概率，从而比较两个均值的差异是否显著。Z检验适用于： 
总体呈正态分布。
总体方差已知。
样本容量较大。
  
② 案例如下
 
③ 有个人说：鸢尾花的平均花瓣长度为3.5cm，这种说法可靠吗？假设经过长期大量验证，鸢尾花花瓣长度总体的标准差为1.8cm，我们就可以使用Z检验来验证了。
 
from scipy import stats
iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))
mean = df["petal length (cm)"].mean()
n = len(df)
sigma = 1.8
z = (mean - 3.5) / (sigma / np.sqrt(n))
display(z)
结果如下：
  
④ 单个正态总体均值的假设检验法(t检验：方差未知)
 
  t检验，与Z检验类似，用来判断样本均值是否与总体均值具有显替性差异。不过，t检验是基于t分布的。检验适用于： 
总体呈正态分布。
总体方差未知。
样本容量较小。
  
⑤ 案例说明
 
⑥ 代码演示
 
# 方法一
iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))
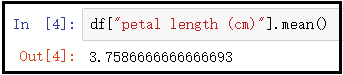
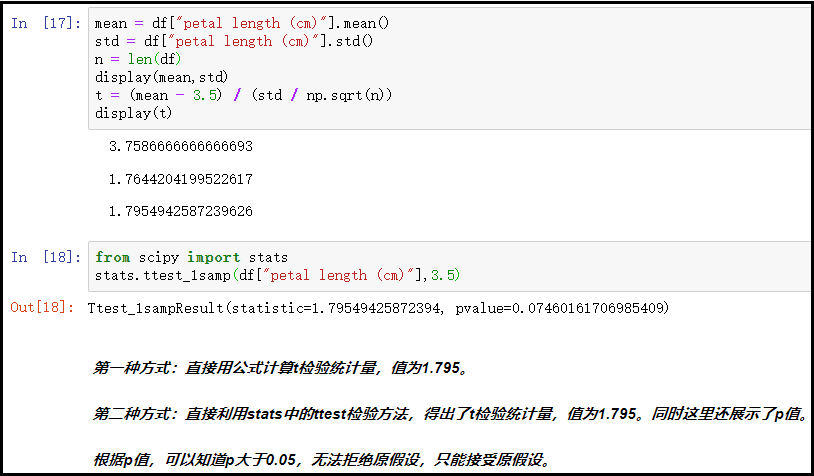
mean = df["petal length (cm)"].mean()
std = df["petal length (cm)"].std()
n = len(df)
display(mean,std)
t = (mean - 3.5) / (std / np.sqrt(n))
display(t)
# 方法二
from scipy import stats
stats.ttest_1samp(df["petal length (cm)"],3.5)
结果如下：
 
                                    统计推断-经典统计推断基本问题统计学与概率论贝叶斯统计与经典统计推断模型与推断变量术语解释经典参数估计术语最大似然估计均值和方差的估计置信区间求近似的置信区间基于方差近似估计量的置信区间线性回归最小二乘法合理性贝叶斯线性回归多元线性回归非线性回归线性规划注意事项简单假设检验内曼-皮尔逊引理显著性检验广义似然比和拟合优度检验
统计推断是什么？
统计推断是从观测数据推断未知变量或未知模型的...
u分布：指标准正态分布，是以0为平均值，以1为标准差的正态分布
z分布：泛指正态分布，是以u为平均值，以西格玛为标准差的正态分布。对于z分布中的所有变量X，转换为（X-U）/西格玛时，其服从u分布。即标准正态分布。
t分布：t分布的均值为0
（参考链接）：https://www.applysquare.com/topic-cn/TZVQpbknE/
1》t分布是正态分布的小样...
                                    统计学被广泛的应用于各个领域之上，从物理和社会科学，再到人文科学，甚至被用在工商业及ZF的情报决策当中。统计学又可分为描述统计学和推断统计学，那么要怎样来区分她们呢？  
　　我们先来了解描述统计学和推断统计学的概念：
描述统计学(descriptive statistics)是研究如何取得反映客观现象的数据,并通过图表形式对所搜集的数据进行加工处理和显示,进而通过综合概括与分析得出反
                                    在统计推断中有两类问题，一类为估计问题，一类为假设检验。估计问题中主要包括**点估计**和**区间估计**，点估计是估计出一个分布中**未知参数的值**，**区间估计则是估计出一个分布中未知参数所在的范围**。
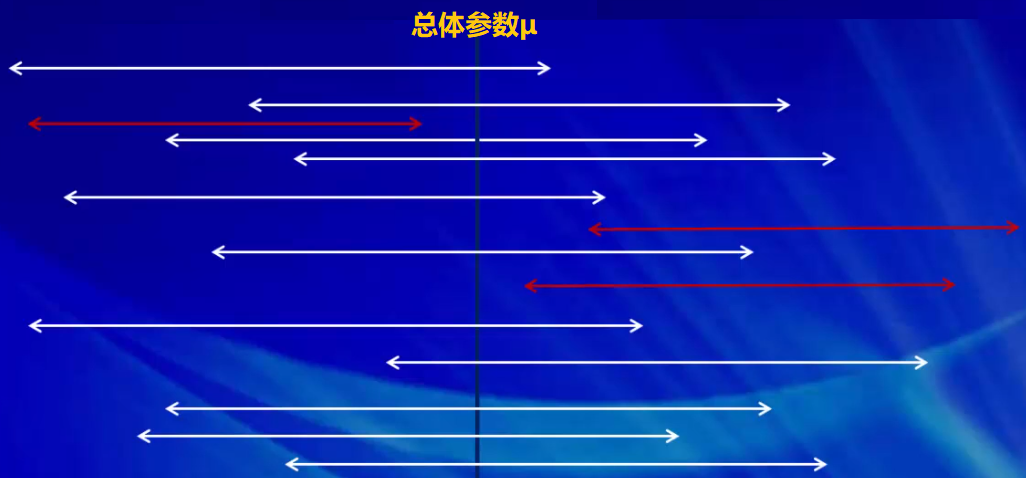
区间估计最终要估计出未知参数所在的区间，这个区间就是经常听到的**置信区间；
T检验，U检验
                                    假设检验和参数估计都是推断统计的重要内容，但是两者的角度不同：
参数估计是利用样本信息推断未知的总体参数；
假设检验是先对总体参数提出一个假设，然后利用信息进行验证。
                                    4.2枢轴量法（续）※两个正态样本有时我们也会比较两个正态总体之间均值或方差有无差异.假设总体  和  是两个相互独立的正态总体，从中分别抽取样本  和  ，相应的统计量如下： 这些分别是两个总体的样本均值、样本方差和偏差平方和.均值之差  的区间估计以下分为几种情形： 两总体方差已知.与单个正态总体完全类似，可以构造枢轴量为 把找常数以及改写不等式的步骤省略，这里直接给出置信水平为  的置信区间...
                                    方差分析的零假设是：各组均值相等。这个“各组均值相等”如何理解？正确理解是：各组和所有组总均值相等，并不是真的“各组均值相等”。方差分析认为：各组和总均值无差异，那么各组均值等于总均值，意味着各组均值相等。单因素方差分析大家应该都理解的比较好，我们可以看看单因素方差分析F检验统计量的分子核心部分：（各组均值-总均值）的平方。看到没，减的是“总均值”。一般来说，如果各组和总均值无差异，那么各组之间也...
                                    -点击上方“中国统计网”订阅我吧！-背 景假如你们现在针对用户提出了三种提高客单价的策略A、B、C，现在想看一下这三种策略最后对提高客单价的效果有什么不同，那我们怎么才能知道这三种策略效果有什么不同？最简单的方法就是做一个实验，我们可以随机挑选一部分用户，然后把这些用户分成三组A、B、C组，A组用户使用A策略、B组用户使用B策略、C组用户使用C策略，等策略实施一段时间以后，我们来看一下...
推论统计是统计学乃至于心理统计学中较为年轻的一部分内容。它以统计结果为依据，来证明或推翻某个命题。具体来说，就是通过分析样本与样本分布的差异，来估算样本与总体、同一样本的前后测成绩差异，样本与样本的成绩差距、总体与总体的成绩差距是否具有显著性差异。例如，我们想研究教育背景是否会影响人的智力测验成绩。可以找100名24岁大学毕业生和100名24岁初中毕业生。采集他们的一些智力测验成绩。用推论统计方法进行数据处理，最
                                    来自正态分布的样本平均数的分布符合N(μ,σ^2/n),即使总体分布不符合正态分布，抽样次数足够大时，样本平均数的分布也符合正态分布。假设检验又称为显著性检验，根据总体的理论分布和小概率原理，对未知或者不完全知道的总体提出两种对立的假设，然后根据样本统计数进行计算，统计推断是 依据总体理论分布（u分布、t分布、二项分布、泊松分布、卡方分布、F分布等），从样本的统计数对总体的参数做出推断。统计可以分为两块，一是统计描述，就是你的数据长什么样子，二是统计推断，就是根据你的数据讨论下理论总体长什么样子。
                                    推断统计是研究如何利用样本数据来推断总体特征的统计方法。包含参数估计和假设检验。参数估计即利用样本信息推断总体特征，也就是根据样本数据来估计变量的概率分布，或者是总体分布所包含的未知参数的过程。举个例子：要研究人们的市场消费行为，首先需要了解人们的收入状况，若某城市人均年收入数据服从正态分布，但参数的均值和方差的具体取值未知，此时就可以根据样本的来估计这两个参数。方法有点估计和区间估计。通俗理解，...
                                    假设检验是统计推断的另一个重要的应用，在分布未知或部分已知的情况下提出对总体的某种假设，比如总体的数学期望，方差以及分布。与参数估计类似，需要基于假设找到适合的检验统计量，通过计算检验统计量的值来确定是否接受假设。通常在方差已知的情况下我们用Z检验来检验关于均值的估计，在方差未知的情况下用T检验检验关于均值的估计，用卡方检验单个总体方差假设，用F检验来检验多个总体的方差假设。在参数估计中我们提到了...
                                    方差分析（Analysis of Variance，ANOVA）就是用于检验两组或两组以上的均值是否具有显著性差异的数理统计方法。有单因素方差分析和多因素方差分析。1 基本原理在方差分析中，把要分析的变量称为响应变量，对响应变量取值有影响的其它变量称为因素，因素的不同取值称为水平。1.1 方差分析的模型以一个单因素的例子进行分析。四种用于缓解手术后疼痛的药品，研究它们的治疗效果是否存在显著性差异。...