无论是线性回归还是逻辑回归都有一个缺点:当特征太多的时,计算负荷会非常大。例如在图片识别的模型中,由于每个像素都是255个特征,而一个50×50像素的小图片,都拥有巨大量的特征,普通的逻辑回归模型,不能有效处理这么多特征,这时我们需要神经网络算法。

如图所示,神经网络模型分为:输入层、中间层(隐藏层)、输出层。
神经网络模型是逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。
神经网络模型由多个神经元组成,而每个神经元是一个个学习模型,这些神经元又叫激活单元,使用Sigmoid函数激活作为下一层的输入。
神经网络本质:逻辑回归单元的叠加。

前向传播算法也叫逻辑回归迭代,如图所示,x加上偏执后的a(1)与θ(1)相乘,得到z(2)作为第二层的输入,通过Sigmoid逻辑函数g(z(2)),得到第二层的输入项a(2),此变量继续作为下一层的输入项继续参与运算。
同时可以把a0,a1,a2,a3看成更为高级的特征值,也就是x0,x1,x2,x3的进化体,并且它们是由x与决定的,因为是梯度下降的,所以a是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将x次方厉害,也能更好的预测新数据。
在神经网络中,原始特征只是输入层,在三层的神经网络例子中,第三层也就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。
按这种方法我们可以逐渐构造出越来越复杂的函数,也能得到更加厉害的特征值
神经网络的代价函数比逻辑回归更加复杂一些,但代价函数背后的思想还是一样的,我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出 K 个预测,基本上我们可以利用循环,对每一行特征都预测 K 个不同结果,然后在利用循环在 K 个预测中选择可能性最高的一个,将其与 y 中的实际数据进行比较。

之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层
开始正向一层一层进行计算,直到最后一层的 hθ(x)。
现在,为了计算代价函数的偏导数 ,我们需要采用一种反向传播算法,也
就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。


前向传播算法的目的是为了得到预测值a,在上图中a(1)a(2)a(3)a(4)都为每层的预测值,其中a(4)为最终预测值也就是h(θ),g(z(4))。

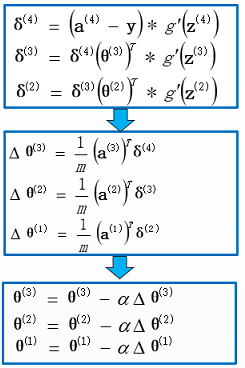
如图,代价函数对theta求偏导,属于复合函数求偏导。我们引出新的参数δ来表示误差。由于各参数的shape,下图为最终的矩阵表示

神经网络算法的代价函数为交叉熵代价函数,由于a4为最终预测值也为h(4),和交叉熵代价函数中的h(θ)为同一个,在对z4求偏导的过程中,引入中间变量a4建立了z4的关联,经过一系列运算解得δ(4)=a(4)-y,正好为预测值和实际值的误差,而在求δ(3)的过程则运用了链式求导法则,在δ4的基础上再通过a(3)建立中间连接,进一步对z(3)进行复合求导。

一句话总结:
即首先正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
import numpy as np
import matplotlib.pyplot as plt
X1 = [0.697,0.774,0.634,0.608,0.556,0.403,0.481,0.437,0.666,0.243,0.245,0.343,0.639,0.657,0.360,0.593,0.719]
X2 = [0.460,0.376,0.264,0.318,0.215,0.237,0.149,0.211,0.091,0.267,0.057,0.099,0.161,0.198,0.370,0.042,0.103]
Y = [1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0]
#数据提取
X = np.c_[X1,X2]
y = np.c_[Y]
def preprocess(X,y):
m = len(X)
np.random.seed(3)
order = np.random.permutation(m)
X = X[order]
y = y[order]
#标准化特征缩放
X -= np.mean(X,axis=0)
X /= np.std(X,axis=0,ddof=1)
X = np.c_[np.ones(len(X)),X]
y = np.c_[y]
return X,y
X,y = preprocess(X,y)
#数据集切分 前70%为训练集 后30%为测试集
m = len(X)
d = int(m*0.7) #避免出现小数 使用int强转
train_X,test_X = np.split(X,[d])
train_y,test_y = np.split(y,[d])
#----------------以上为数据预处理操作-------------------
#逻辑函数 设置deriv参数便于求导数 (关于逻辑函数的求导 是复合函数求导 一步步慢慢算)
def g(z,deriv=False):
if deriv == True:
return z*(1-z)
return 1/(1+np.exp(-z))
#模型 正向传播算法
def model(X,theta1,theta2,theta3):
a1 = X
z2 = np.dot(a1,theta1)
a2 = g(z2)
z3 = np.dot(a2,theta2)
a3 = g(z3)
z4 = np.dot(a3,theta3)
a4 = g(z4)
return a2,a3,a4
#反向传播算法
def BP(a1,a2,a3,a4,y,theta1,theta2,theta3,alpha):
#求delta值
delta4 = a4 - y
delta3 = np.dot(delta4,theta3.T)*g(a3,deriv=True)
delta2 = np.dot(delta3,theta2.T)*g(a2,deriv=True)
#求deltaTheta
deltaTheta3 = 1.0/m*np.dot(a3.T,delta4)
deltaTheta2 = 1.0/m*np.dot(a2.T,delta3)
deltaTheta1 = 1.0/m*np.dot(a1.T,delta2)
#更新theta
theta3 -= alpha*deltaTheta3
theta2 -= alpha*deltaTheta2
theta1 -= alpha*deltaTheta1
return theta1,theta2,theta3
#代价函数
def costFunc(h,y):
m = len(y)
#交叉熵代价函数(注意负号)
J = -1.0/m*np.sum(y*np.log(h)+(1-y)*np.log((1-h)))
return J
def gradDesc(X,y,hidden_layer_size=(17,8),alpha=0.1,iter_num=20000):
m,n = X.shape
k = y.shape[1]
#初始化theta(以防出现负号)
theta1 = 2*np.random.rand(n,hidden_layer_size[0])-1
theta2 = 2*np.random.rand(hidden_layer_size[0],hidden_layer_size[1])-1
theta3 = 2*np.random.rand(hidden_layer_size[1],k)-1
#初始化代价
J_history = np.zeros(iter_num)
for i in range(iter_num):
#求预测值
a2, a3, a4 = model(X,theta1,theta2,theta3)
#记录代价
J_history[i] = costFunc(a4,y)
theta1, theta2, theta3 = BP(X,a2,a3,a4,y,theta1,theta2,theta3,alpha)
return J_history,theta1, theta2, theta3
#评价模型好坏 准确率
def score(h,y):
m = len(h)
count = 0
for i in range(m):
if np.where(h[i]>=0.5,1,0) == y[i]:
count += 1
return count/m
#训练集放在模型进行 参数训练
J_history,theta1, theta2, theta3 = gradDesc(train_X,train_y)
#画代价曲线
plt.plot(J_history)
plt.show()
#训练集预测值 测试集预测值
train_a2,train_a3,train_h = model(train_X,theta1,theta2,theta3)
test_a2,test_a3,test_h = model(test_X,theta1,theta2,theta3)
print('测试集准确率为',score(test_h,test_y))
#输出结果为-----
#测试集准确率为 1.0
神经网络算法的调库实现
初识神经网络1、神经网络模型如图所示,神经网络模型分为:输入层、中间层(隐藏层)、输出层。神经网络模型是逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。神经网络模型由多个神经元组成,而每个神经元是一个个学习模型,这些神经元又叫激活单元,使用Sigmoid函数激活作为下一层的输入。神经网络本质:逻辑回归单元的叠加。2、前向传播算法( FORWARD PROPA...
BP误差反向传播算法
BP(Back Propagation)算法是有监督情况下进行训练神经网络中权重系数的重要方法。神经网络是判别模型的重要组成部分。而判别模型又是模式识别的一大块。关系如下图
BP算法由Rumelhart和McClelland于1985年提出。核心思想是利用输出后的误差来估计输出层的前一层的误差,再用这个误差设计更前一层的误差,如此一层一层地反向传播下去,从而获得其他各...
训练集是一组有输入,且知道正确输出的数据。
训练的过程即通过这组数据,构建一个函数,使在同样的输入下,这个函数的输出与真实的输出之间的差距尽量小。
这个函数即为预测函数,是我们最终用机器学习到的“知识”。
而评价这个函数的输出与真实的输出之间的差距的准绳我们称之为LOSS,它也是一个函数,针对不同的问题,有各种不同的确定方法。
梯度下降方法:
如图所示,即从
神经网络可以采用有
监督和无
监督两种方式来进行训练。传播训练
算法是一种非常有效的有
监督训练
算法。6种传播
算法如下:
1·Backpropagation Training
2·Quick Propagation Training (QPROP)
3·Manhattan Update Rule
NLP工程师需要掌握多种机器学习算法的代码实现,以下是几种常见的算法及其实现方式:
1. 朴素贝叶斯算法:该算法是一种基于概率的分类方法,可用于文本分类等任务。代码实现可以用Python中的sklearn库进行,具体可参考sklearn.naive_bayes模块。
2. 隐马尔可夫模型:该模型是一种基于状态序列和观测序列的概率模型,可用于词性标注、语音识别等任务。代码实现可以参考Python中的hmmlearn库。
3. 支持向量机算法:该算法是一种分类和回归算法,通过找到最优的分割超平面将数据进行分类或回归。代码实现可以用Python中的sklearn库进行,具体可参考sklearn.svm模块。
4. 决策树算法:该算法通常用于分类问题,通过构建一棵决策树将数据进行分类,可以使用Python中的sklearn库进行代码实现,具体可参考sklearn.tree模块。
5. 深度学习算法:深度学习是一种通过多层神经网络来进行模式识别和分类的算法,包括卷积神经网络、循环神经网络等。代码实现可以使用Python中的TensorFlow、Keras、PyTorch等深度学习框架,根据不同的任务进行选择。
综上所述,NLP工程师需要熟练掌握多种机器学习算法的代码实现,选择不同的算法根据具体的任务需求进行调整和优化,以达到最理想的效果。








