信号的傅里叶变换后的虚数怎样理解？

为了引出这个傅里叶变换后复信号的话题,我们仍然先来看看信号狗中最广为流传的傅里叶变换,如果你不熟悉这一方面的知识,你可以在下面的回答中快速将傅里叶变换的内容过一遍

如果你已经熟悉了傅里叶变换,那么事情就好说了,我们仍然回到经典的欧拉公式中来

e^{j\theta}=cos\theta+jsin\theta (式1.0)

该函数将复数、指数函数与三角函数相互联系起来。如果定义一个复平面，其中以横坐标方向作为实数方向，纵坐标方向作为虚数方向，这种式子又叫复变函数,它实际上是一个绕原点旋转的一个圆，如下图：

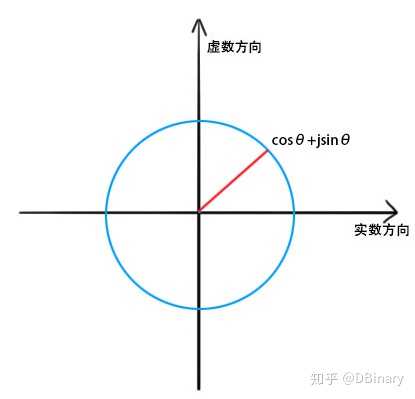
由公式:

\theta=wt=\frac{2\pi}{T}t (式1.1)

可知，该复变函数可以看做是一个角速度为 w 周期为 T 在复平面上绕原点旋转的半径为1的圆。将公式代回到复变函数中，那么，复变函数可以写成公式1.2的形式

e^{jwt}=cos(wt)+jsin(wt) (式1.2)

设一组三角函数，其频率是 cos(wt) 的n倍，其中n是大于0的正整数，那么可以定义这一组三角函数为：

cos(nwt)=\frac{e^{jnwt}+e^{-jnwt}}{2} (式1.3)

sin(nwt)=\frac{e^{jnwt}-e^{-jnwt}}{2j} (式1.4)

我们知道傅里叶级数写成下面这种形式

f(t)=c_{0}+\sum_{n=1}^{\infty}{[a_{n}cos(nwt)+b_{n}sin(nwt)]} (式1.5)

将公式1.3与1.4代回到式1.5中，可得到如下公式

f(t)=c_{0}+\sum_{n=1}^{\infty}{[a_{n}\frac{e^{jnwt}+e^{-jnwt}}{2}+b_{n}\frac{e^{jnwt}-e^{-jnwt}}{2j}]}

进一步化简,得到

f(t)=c_{0}+\sum_{n=1}^{\infty}{[\frac{a_{n}-jb_{n}}{2}e^{jnwt}+\frac{a_{n}+jb_{n}}{2}e^{-jnwt}]} (式1.6)

根据开头文章的推论,因为

a_{-n}=\frac{2}{T}\int_{}^{T}f(t)cos(-nwt)dt=a_{n}

b_{-n}=\frac{2}{T}\int_{}^{T}f(t)sin(-nwt)dt=-b_{n}

因此式1.6进一步可以写成:

f(t)=c_{0}+\sum_{n=1}^{\infty}{[\frac{a_{n}-jb_{n}}{2}e^{jnwt}+\frac{a_{-n}-jb_{-n}}{2}e^{-jnwt}]}

即

f(t)=c_{0}+\sum_{n=1}^{\infty}{[\frac{a_{n}-jb_{n}}{2}e^{jnwt}]+\sum_{n=-\infty}^{-1}[\frac{a_{n}-jb_{n}}{2}e^{jnwt}]}

其中, c_{0} 作为直流分量,对应n=0的情况,因此上次可合并为

f(t)=c_{0}+\sum_{n=-\infty}^{\infty}{\frac{(a_{n}-jb_{n})}{2}}e^{jnwt}

这个时候,只要设

A_{n}=\frac{(a_{n}-jb_{n})}{2}

我们就得到了一个复数形式的傅里叶级数

f(t)=\sum_{n=-\infty}^{\infty}{A_{n}e^{jnwt}} (式1.7)

我们对式4.7两边同时乘以一个 e^{jnwt} ,并对它们在一个周期内进行积分,得到式子

\int_{}^{T}f(t)e^{-jkwt}dt=\int_{}^{T}\sum_{n=-\infty}^{\infty}{A_{n}e^{j(n-k)wt}}dt

由正交性可知,当n与k不相等时,积分结果必定为0,仅当 n=k 时,右表达式有值,因此,推导出

\int_{}^{T}f(t)e^{-jkwt}dt=A_{n}T

即得出复信号 A_{n} 的求法,也就是我们常见的复变函数形式的傅里叶变换了

A_{n}=\frac{1}{T}\int_{}^{T}f(t)e^{-jkwt}dt

好了,到这里有啥用呢,因为我们知道了

A_{n}=\frac{(a_{n}-jb_{n})}{2}

所以,如果我们要求幅值,只要求复信号 A_{n} 的模就行了

\left| A_{n} \right|=\frac{1}{2}\sqrt{a_{n}^{2}+b_{n}^{2}}=\frac{1}{2}c_{n}

你看,刚好是幅值的一半,同理,依据

e^{jwt}=cos(wt)+jsin(wt)

虚部为sin,实部为cos要求相位也只需要

\varphi=arctan(\frac{b_{n}}{a_{n}})

就行了。