定理1：任一个具有N个结点的连通图，它的任何一个树的树枝数为N-1。
定理2：对于一个具有b条支路和
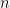个结点的电路，连支数
。
定理3：具有N个节点的电路，在任意N-1个结点上可以列出N-1个独立的KCL方程。
证明定理2：因为“树支数+连支数=总支路数”，即：
，所以
问题1：内网孔数=连支数=独立方程数？
答：此结论对平面电路图是成立的。只有对平面图才会引入网孔的概念。
问题2：如果是一个非平面图，如何确定独立方程数？定理1和定理2还适用吗？
答：非平面图，要根据定理1和定理2来确定独立方程数，定理1和定理2依然适用。
总结1：连支数决定了基本回路组，而基本回路组对应于KVL的独立方程数。
电路之KCL和KVL的独立方程数总结
定理1：任一个具有N个结点的连通图，它的任何一个树的树枝数为N-1。定理2：对于一个具有b条支路和个结点的电路，连支数。定理3：具有N个节点的电路，在任意N-1个结点上可以列出N-1个独立的KCL方程。证明定理2：因为“树支数+连支数=总支路数”，即：，所以 。证毕。问题1：内网孔数=连支数=独立方程数？答：此结论对平面电路图是成立的。只...
这是困惑了本人很久的问题，最近得闲，去b站观光了部分的离散
数
学课程并参考了一些资料，对这个问题做个
总结
，也算是笔记吧。
电路
原理和离散
数
学都还没学完，小白一只，各位如有发现任何错误，恳请指出。
支路电流法解线性
电路
的一般方法
已知在求解线性
电路
的过程当中，可以列出n-1条
kcl
独立
的
kcl
方程
，b-（n-1）条
kvl
独立
的
方程
，从而可以解出b条支路的电压电流参
数
。作为一般性的理论，在
电路
的求解过程当中常会用到。但我们是否有思考过，为什么
电路
的节点之中一定就能够找到n-1条
kcl
方程
呢？下面用图论的割集理论对这
利用一下基本公式：
1.I=dqdt1.I=\frac{dq}{dt}1.I=dtdq
2.C=eS4πkd=qU2.C=\frac{eS}{4\pi kd}=\frac{q}{U}2.C=4πkdeS=Uq
3.I=UR3.I=\frac{U}{R}3.I=RU
从而由
电路
的1.串联分压2.整个
电路
电流相等，可以得到
KVL
方程
：
Us=uc(t)+Ri(t)=uc(t)+Rdq(t)dt=uc(t)+RdCuc(t)dt=uc(t)+RCduc(t)dtU_s=u_c(t)+Ri(t)=u_c(.
电力（一级学科）；通论（二级学科）
2.在一个无向连通图G中，生成树的树枝
数
取决于节点
数
n，b(T)=n-1;
一个树T的基本割集
数
取决于树枝
数
，基本割基
数
=树枝
数
，每一个割集有且仅有一个树枝;
基本割集的确定：从树T中删除一个树枝，...
KCL
和
KVL
的
独立
方程
可以证明，对于具有n个节点(顶点)的
电路
，在任意(n-1)个节点(定点)上可以得出(n-1)个
独立
的
KCL
方程
。相应的(n-1)个节点称为
独立
节点。
将对应于一组线性
独立
的
KVL
方程
的回路称为
独立
回路，回路和
独立
回路的概念与支路的方向无关，因此可以用无向图的概念叙述。
当图(Graph)的任意两个结点(顶点)之间至少存在一条路径时，图就称为连通图。如果一条路径的起点
支路电流法是
电路
分析中最基本的方法之一， 但是当支路
数
较多时，所需要的
方程
的
个数
较多，求解不方便。
方程
组的
个数
=网孔的
个数
自电阻* 配角电流 - 互电阻*主角电流==电源产生的沿网孔方向的压升之和
基尔霍夫（
电路
）定律(Kirchhoff laws)是
电路
中电压和电流所遵循的基本规律，是分析和计算较为复杂
电路
的基础，1845年由德国物理学家G.R.基尔霍夫（Gustav Robert Kirchhoff，1824～1887）提出。基尔霍夫（
电路
）定律包括基尔霍夫电流定律（
KCL
）和基尔霍夫电压定律（
KVL
）。
基尔霍夫（
电路
）定律既可以用于直流
电路
的分析...
