7.1 涉及的专业名词解释

7.1.1 估计量与估计值_名词解释

📌 参数估计
用样本统计量去估计总体的参数。

📌 估计量
用来估计总体参数的统计量称为估计量，用 $表示。样本均值、样本比例、样本方差都可以是一个估计量。$

📌 估计值
根据一个具体的样本计算出来的估计量的数值，称为估计值。比如用样本量计算出来的平均值作为总体的平均值，那么这个平均值在这时就称为估计值。

7.1.2 点估计与区间估计

💡 excel中计算指定概率对应的面积公式：= normsinv (指定的概率)
例：当显著性为5%时， $的估计值。$

📖 在重复抽样条件下，点估计的均值可望等于总体真值。

由于样本是随机的，抽出一个具体的样本得到的估计值很可能不同于总体真值，所以在使用点估计代表总体参数值时，需要给出点估计值的可靠性，即说明点估计值与总体参数的真实值的接近程度。

由于点估计值的可靠性由抽样标准误差衡量，所以具体的点估计值无法给出估计可靠性的度量，故需要围绕点估计值构造总体参数的一个区间，这是区间估计。

📌 区间估计
给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。

📖 与点估计不同，区间估计时，根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给出一个概率度量。

📌 置信区间
样本统计量所构成的总体参数的估计区间称为置信区间，其中区间的最小值称为置信下限，最大值称为置信上限。

可以理解为假设在需要估计GMV，估计的正确率需要达到95%，在95%的概率下计算出来GMV处于[100,101]，得出的这个区间就是置信区间。

📌 置信水平
置信区间中包含总体参数真值的次数所占的比例称为置信水平，也称为置信度，表示为

可以理解为参数估计的正确率，如上述GMV例子中的95%。

📖 样本量、置信水平与置信区间的关系
当样本量给定时，置信区间的宽度随着置信水平的增大而增大；
当置信水平固定时，置信区间的宽度随着样本量的增大而减小，即较大的样本所提供的有关总体的信息更多。

📖 对置信区间的理解，有3点需注意：

怎么理解置信水平为95%的置信区间？
如果用某种方法构造的所有区间中有95%的区间包含总体样本的真值，5%的区间不包含总体参数的真值，那么用该方法构造的区间称为置信水平为95%的置信区间。
置信区间会因为样本不同而不同；
总体参数的真值是固定的、未知的，而样本构造的区间是不固定的。所以 置信区间 是一个随机区间，会 因为样本的不同而不同 ，而且不是所有的区间都包含总体参数的真值。
置信水平是针对随机区域而言的；
不是用来描述某个特定区间包含总体参数真值的可能性。

比如某班级学生平均考试成绩置信水平为95%的置信区间为[60,80]，不能说60~80分以95%的概率包含全班学生平均考试的真值。我们只知道在多次抽样中，95%的样本得到的区间包含全班学生平均考试成绩的真值。

7.1.3 评价估计量的标准

📌 无偏性

样本期望与总体参数无偏，即估计量抽样分布的数学期望等于被估计量总体参数；
设总体参数为

当样本均值的期望值等于总体均值，样本比例的期望值等于总体比例，那么样本方差的期望值等于总体误差。

📌 有效性
更小标准差的估计量更有效；对同一总体参数的两个无偏估计量，有更小标准差的估计量更有效。

📌 一致性
估计量与总体一致；随着样本量的增大，估计量的值越来越接近被估总体的参数，即样本量越大，标准差应该越小

7.2 如何估计一个总体参数的范围，及如何选择对应的分布公式？

总体思路：
根据样本和总体数据集的情况，以及需要求的参数是什么，来选择不同的分布公式。将指标带入公式计算，则得到总体的参数估计量。

比如：想通过样本数据集，求总体的均值是多少。如果样本数据集是大样本，则选择Z分布的公式；如果是小样本，则需要看总体的方差是否已知，如果总体方差不可得，则选择t分布的公式。

☑️ 对不同的参数进行估计，对应选择的不同分布

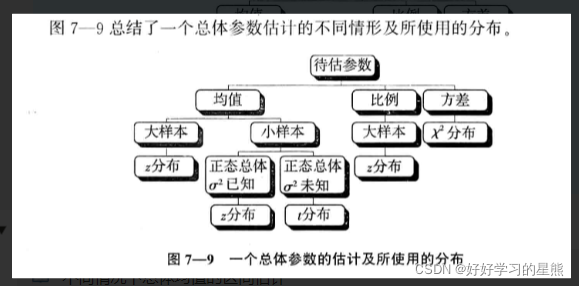
7.2.1 如何对总体均值的区间进行估计？

📖 不同情况下总体均值的区间估计公式

💡 z分布区间计算的excel公式：

=avg(样本值)± normsinv (1-$\alpha/

📖 t分布
类似正态分布的一种对称分布，通常比正态分布平坦和分散，一个特定的t分布依赖于称之为自由度的参数。随着自由度的增大，t分布逐渐趋于正态分布。

7.2.2 如何对总体比例的区间进行估计？

📖 本章内容的前提条件：
此节只讨论大样本情况的总体比例的估计问题。

对于总体比例的估计，确定样本是否足够大的一般经验规则是：
区间

7.3 如何估计两个总体参数的区间范围，及如何选择对应的分布公式？

7.3.1 如何估计两个总体的均值之差的区间范围？

📖 情况一：独立大样本时
如果两个样本是从两个总体中独立抽取，且两个总体都为正态分布；或两个总体不服从正态分布，但两个样本都是大样本（n≥30）。

其中总体均值为 $z=\frac {(\bar{x}_1-\bar{x}_2)-(\mu_1-\mu_2)} {\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim{N(0,1)}$

🔑 当两个总体的方差 $(\bar{x}_1-\bar{x}_2)\pm z_{\alpha/2}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

🔑 当两个总体的方差 $t=\frac{(\bar{x}_1-\bar{x}_2)-(\mu_1-\mu_2)} {s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim{t(n_1+n_2-2)}$

两个总体均值之差在 $(\bar{x}_1-\bar{x}_2)\pm t_{\alpha/2}(n_1+n_2-2) \sqrt{ s_p^2(\frac{1}{n_1}+\frac{1}{n_2}) }$

🔑 当两个总体方差未知且不相等时，两个样本均值之差经标准化后近似服从自由度为 $v=\frac{ (\frac{s_1^2}{n_1} +\frac{s_2^2}{n_2})^2 }{ \frac{(s_1^2/n_1)^2}{n_1-1} +\frac{(s_2^2/n_2)^2}{n_2-1} }$

两个总体均值之差在

独立样本时，每种方法随机指派12个工人，可能会将技术较差的12个工人指定给方法1，技术较好的工人指定给方法2，这种不公平的指派可能会掩盖两种方法组装产品所需时间的真正差异。

匹配样本时，先指定12个工人用第一种方法，然后再让这12个工人用第二种方法，这样得到的数据就是匹配数据。

匹配样本可以消除由样本指定的不公平造成的两种方法组装时间上的差异。

🔑 大样本条件下，均值之差 $Z=\frac{ (p_1-p_2)-(\pi_1-\pi_2) }{ \sqrt{ \frac{\pi_1(1-\pi_1)}{n_1} +\frac{\pi_2(1-\pi_2)}{n_2} }} \sim{ N(0,1) }$

🔑 当两个总体比例 $F_{1-\alpha/2} \le{\frac{s_1^2}{s_2^2}\cdot\frac{\sigma_2^2}{\sigma_1^2}} \le{F_{\alpha/2}}$

🔑 由上式可得，两个总体方差比在 $\frac{s_1^2/s_2^2}{F_{\alpha/2}} \le{\frac{\sigma_1^2}{\sigma_2^2}} \le{\frac{s_1^2/s_2^2}{F_{1-\alpha/2}}}$

的估计值。

📖 样本量与置信水平成正比，置信水平越大，所需的样本量也就越大；
样本量与总体方差成正比，总体的差异越大，要求的样本量也越大；
样本量与估计误差的平方成反比，即可以接受的估计误差的平方越大，所需的样本量越小。

根据公式计算出来的样本数为非整数时，通常取成较大的整数，即样本量的圆整法则。

在重复抽样，或无限总体抽样条件下，估计误差为 $估计量与估计值_名词解释📌 参数估计用样本统计量去估计总体的参数。📌 估计量用来估计总体参数的统计量称为估计量，用θ^\hat{\theta}θ^表示。样本均值、样本比例、样本方差都可以是一个估计量。📌 估计值根据一个具体的样本计算出来的估计量的数值，称为估计值。比如用样本量计算出来的平均值作为总体的平均值，那么这个平均值在这时就称为估计值。7.1.2 点估计与区间估计💡 excel中计算指定概率对应的面积公式：=normsinv(指定的概率)例：$

均数的抽样误差与标准误统计推断（statistical inference)：从总体中随机抽取一个或多个样本，通过样本信息了解总体特征。由于存在个体差异，样本均数的值往往不太可能恰好等于总体均数，因此通过样本推断总体会有误差。抽样误差（sampling error):这种由个体变异产生、随机抽样造成的样本统计量（statistic）与总体参数(parameter)的差异、来自同一总体的若干样本统计量之间的差异。抽样误差不可避免但具有一定规律性。样本均数的分布

文章目录 样本均值 样本方差 样本矩 (moments) 统计学中有一些很重要的度量方式，如同「 概率论 」中用期望、方差评价分布的离散情况一样；在统计学里也使用了相似的概念，比如说「均值」、「方差」，另外还多了一个「样本炬」，现在让我们来看看这些具体的定义吧。 Xˉ=1n∑i=1nxi\bar{X} = \frac{1}{n} \sum_{i=1}^{n} x_iXˉ=n1i=1∑nxi 这个没什么好特别说明的，就是把「样本个体」的值相加后除以「样本总数」得到一个平均值。 S2=D(X)=

如何用样本估计总体？笔记来源：Calculating the Mean, Variance and Standard Deviation, Clearly Explained!!! 将上述结果绘制成直方图直方图对应的正态分布图如下：我们无法测得所有肝脏细胞中基于X的mRNA，我们需要用样本来估计总体，这里我们用240 billion中的5个细胞作为样本，图中每个绿点代表一个细胞，其值代表此细胞中基因X所含mRNA的数量我们看一看当样本数据有2个时，计算出来的 样本均值 与总体均值的差距在哪，样本

总体是在进行统计分析时，研究对象的全部；个体是组成总体的每个研究对象；样本是从总体 X中按一定的规则抽出的个体的全部，用X1，X2，…，XnX_1，X_2，…，X_nX1，X2，…，Xn表示；样本中所含个体的个数称为样本容量，用nnn表示。就好比要研究一个班的平均身高: 这个班的所有同学的身高就是总体； A同学的身高就是1个个体；按一定的规律抽出20个同学的身高研...

参数估计 （Parameter Estimation）人们常常需要根据手中的数据，分析或推断数据反映的本质规律。即根据样本数据如何选择统计量去推断总体的分布或数字特征等。统计推断是数理统计研究的核心问题。所谓统计推断是指根据样本对总体分布或分布的数字特征等作出合理的推断。它是统计推断的一种基本形式，是数理统计学的一个重要分支，分为点估计和区间估计两部分。 参数估计 （Parameter Est...

虽然非计算机专业，但因为一些原因打算学习西瓜书，可由于长时间没有碰过概率统计的知识，有所遗忘。所以特意重新复习了一遍类似的知识，写在这里权当总结。主要参考《 概率论 与数理统计》(陈希孺)。 参数估计 就是根据样本推断总体的均值或者方差、或者总体分布的其他参数。可以分两种，一种是点估计 ( 估计一个参数的值)，另一种是区间估计 ( 估计一个参数的区间)。 参数估计 的方法有多种，各种估计方法得出的结果不一定...