并且有一个被人们称为“筛选性”的性质。顾名思义,对于任意函数f(t),都能筛选出f(t0)的值。
对于δ函数,因为它的取值是0或者无穷,所以我们没办法画出它的图像。我们通常用一个向上的箭头来表示它:
用画图工具大致画了下 关于δ函数具体的形式,有很多种定义方法。例如定义为:
δ函数还有很多性质,如偶函数性和伸缩性质,这些性质结合上式就很容易理解了:
矩形函数(门函数)
矩形函数的形状类似一扇门,故有时候我们也称之为门函数。将非0区间的长度称为门宽。例如下面就是门宽为1的门函数(矩形函数)的定义:
其函数图像如下图所示:
门宽为任意正数 的定义如下:
其函数图像如下图所示:
三角波函数
顾名思义,三角波函数就是一个三角形。
其函数图像如下图所示:
半底宽为任意正数 的定义如下:
其函数图像如下图所示:
sinc函数
sinc函数在信号处理中十分常用,因为它的傅里叶变换是门函数。在数学系的教材中,它的定义通常乘以了一个系数π。而在我们工科,通常不乘以π。本文采用的是工科的定义,具体定义如下:
注意到这个函数在x=0处没有定义,但是该点恰好是一个可去间断点,因此将其极限值1作为该点函数值的定义。即sinc(0)=1 。
其函数图像如下图所示:
我们用x*(t) 代表函数x(t) 的共轭函数。
我们用x1(t)*x2(t) 代表x1(t)和x2(t) 的卷积,即:
傅里叶变换相关符号的定义
数学系通常用符号i作为虚数单位,而我们工科一般用
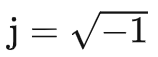 作为虚数单位,本文中所有出现虚数单位的时候都采用j这一符号。并且我们有时候利用关系w=2πf消去逆变换的系数2π。
作为虚数单位,本文中所有出现虚数单位的时候都采用j这一符号。并且我们有时候利用关系w=2πf消去逆变换的系数2π。
我们将自变量为角频率ω的F(w) 函数称为f(t) 的傅里叶变换函数,我们将自变量为频率f的S(f) 函数称为s(t) 的频谱函数。
将傅里叶变换过程用花体符号
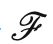 表示:
表示:
将傅里叶逆变换过程用花体符号
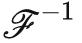 表示:
表示:
比较明显的是:若s(t)与f(t)相同,则有:
考虑到花体符号
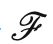 表示对变换关系体现得不是那么显明,因此用下式来表现变换关系会相对更加显明:
表示对变换关系体现得不是那么显明,因此用下式来表现变换关系会相对更加显明:
注意:本文中用到a↔b符号时,均指a的傅里叶变换为b。
频域为ω的傅里叶变换性质大全
我们比较常用的是频域为ω的傅里叶变换,不过这样的变换性质会大量出现常数项(2π)。
若
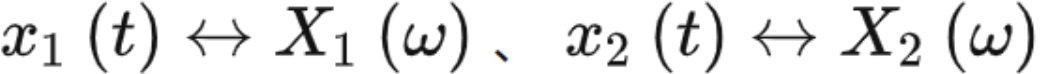 ,a、b为常数,则有:
,a、b为常数,则有:
简单地说,实偶对实偶,实奇对虚奇。即:实偶函数的傅里叶变换是实偶函数,实奇函数的傅里叶变换是虚奇函数。
时域平移性
若
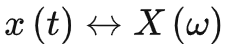 ,则有:
,则有:
频域平移性
若
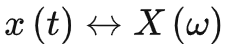 ,则有:
,则有:
尺度变换性
若
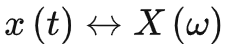 ,对于大于0的常数a,有:
,对于大于0的常数a,有:
若
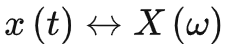 ,有:
,有:
所以
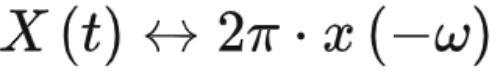 ,将变量名对换即得证。
,将变量名对换即得证。
时域微分性
若
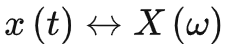 ,有:
,有:
频域微分性
若
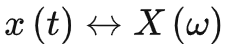 ,有:
,有:
时域积分性
若
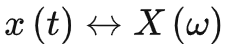 ,有:
,有:
若
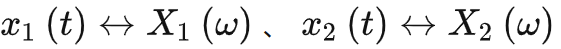 ,有:
,有:
若
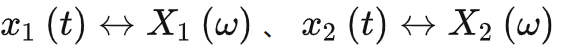 ,有:
,有:
若
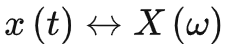 ,有:
,有:
将t=0 代入傅里叶变换的定义:
若
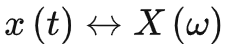 ,有:
,有:
帕塞瓦尔等式
若实函数
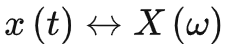 ,有:
,有:
频域为f的傅里叶变换性质大全
对于功率谱的估计,我们有时使用频域为f的傅里叶变换,这样的变换中,一些地方的常数项(2π)会被消掉,因此结果比较简明。
4.1、线性性质
若、 ,a、b为常数,则有:
4.2、共轭性质
简单地说,实偶对实偶,实奇对虚奇。即:实偶函数的傅里叶变换是实偶函数,实奇函数的傅里叶变换是虚奇函数。
4.3、时域平移性
若 则有:
4.4、频域平移性
若 则有:
4.5、尺度变换性
若 ,对于大于0的常数a,有:
4.6、对偶性
若 ,有:
4.7、时域微分性
若 ,有:
4.8、频域微分性
若 ,有:
4.9、时域积分性
若 ,有:
4.10、时域卷积
若 、 ,有:
4.11、频域卷积
若 、 ,有:
4.12、时域初值
若 ,有:
4.13、频域初值
若 ,有:
4.14、帕塞瓦尔等式
若实函数 ,有:
傅里叶对大全
x(t)<->X(f)的变换对根据对偶性很好记。
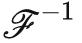 表示:
表示: