然后,打开工程,新建 DSP_LIB 分组,并将 arm_cortexM4lf_math.lib 添加到工程里面,如图:
2, 添加头文件包含路径
添加好.lib 文件后,我们要添加头文件包含路径,将第一步拷贝的 Include 文件夹和 DSP_LIB文件夹,加入头文件包含路径。
3, 添加全局宏定义
最后,为了使用 DSP 库的所有功能,我们还需要添加几个全局宏定义:
1,__FPU_USED
2,__FPU_PRESENT
3,ARM_MATH_CM4
4,__CC_ARM
5,ARM_MATH_MATRIX_CHECK
6,ARM_MATH_ROUNDING
添加方法:点击C/C++选项卡,然后在 Define 里面进行设置,如图
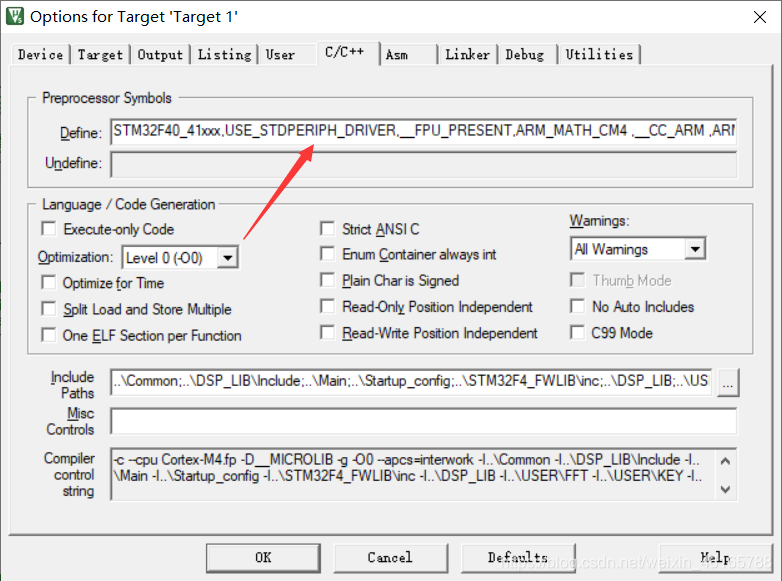
这里,两个宏之间用“,”隔开。并且,上面的全局宏里面,我们没有添加__FPU_USED,因为这个宏定义在 Target 选项卡设置 Code Generation 的时候,选择了:Use FPU(如果没有设置 Use FPU,则必须设置!!),故 MDK 会自动添加这个全局宏,因此不需要我们手动添加了。
至此,STM32F4 的 DSP 库运行环境就搭建完成了。
FFT介绍
FFT 即快速傅里叶变换,可以将一个时域信号变换到频域。因为有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了,这就是很多信号分析采用 FFT 变换的原因。另外,FFT 可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。简而言之,FFT 就是将一个信号从时域变换到频域方便我们分析处理。
照一定大小采样频率 F 去采集信号,采集 N 个点,那么通过对这 N 个点进行 FFT 运算,就可以得到这个信号的频谱特性。 这里还涉及到一个采样定理的概念:在进行模拟/数字信号的转换过程中,当采样频率 F 大于信号中最高频率 fmax的 2 倍时(F>2*fmax),采样之后的数字信号完整地保留了原始信号中的信息,采样定理又称奈奎斯特定理。举个简单的例子:比如我们正常人发声,频率范围一般在 8KHz以内,那么我们要通过采样之后的数据来恢复声音,我们的采样频率必须为 8KHz 的 2 倍以上,也就是必须大于 16KHz 才行。
模拟信号经过 ADC 采样之后,就变成了数字信号,采样得到的数字信号,就可以做 FFT变换了。N 个采样点数据,在经过 FFT 之后,就可以得到 N 个点的 FFT 结果。为了方便进行FFT 运算,通常 N 取 2 的整数次方。
假设采样频率为 F,对一个信号采样,采样点数为 N,那么 FFT 之后结果就是一个 N 点的复数,每一个点就对应着一个频率点(以基波频率为单位递增),这个点的模值(sqrt(实部虚部2))就是该频点频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为 A,那么 FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是 A 的 N/2倍,而第一个点就是直流分量,它的模值就是直流分量的 N 倍。
这里还有个基波频率,也叫频率分辨率的概念,就是如果我们按照 F 的采样频率去采集一个信号,一共采集 N 个点,那么基波频率(频率分辨率)就是 fk=F/N。 这样,第 n 个点对应信号频率为:F*(n-1)/N;其中 n≥1,当 n=1 时为直流分量。
关于 FFT 就介绍到这。
官方FFT使用
如果我们要自己实现 FFT 算法,对于不懂数字信号处理的朋友来说,是比较难的,不过,ST 提供的 STM32F4 DSP 库里面就有 FFT 函数给我们调用,因此我们只需要知道如何使用这些函数,就可以迅速的完成 FFT 计算,而不需要自己学习数字信号处理,去编写代码了,大大方便了我们的开发。STM32F4 的 DSP 库里面,提供了定点和浮点 FFT 实现方式,并且有基 4的也有基 2 的,大家可以根据需要自由选择实现方式。注意:对于基 4 的 FFT 输入点数必须是 4n,而基 2 的FFT 输入点数则必须是 2n,并且基 4 的 FFT 算法要比基 2 的快。 本次我将采用 DSP 库里面的基 4 浮点 FFT 算法来实现 FFT 变换,并计算每个点的幅值、频率、相位。
所用到的函数有:
arm_status arm_cfft_radix4_init_f32(
arm_cfft_radix4_instance_f32 * S,
uint16_t fftLen,uint8_t ifftFlag,uint8_t bitReverseFlag)
void arm_cfft_radix4_f32(const arm_cfft_radix4_instance_f32 * S,float32_t * pSrc)
void arm_cmplx_mag_f32(float32_t * pSrc,float32_t * pDst,uint32_t numSamples)
第一个函数 arm_cfft_radix4_init_f32,用于初始化 FFT 运算相关参数,其中:fftLen 用于指定 FFT 长度(16/64/256/1024/4096),本章设置为1024;ifftFlag 用于指定是傅里叶变换(0)还是反傅里叶变换(1),本次设置为0;bitReverseFlag 用于设置是否按位取反,本章设置为 1;最后,所有这些参数存储在一个 arm_cfft_radix4_instance_f32 结构体指针 S 里面。
第二个函数 arm_cfft_radix4_f32 就是执行基 4 浮点 FFT 运算的,pSrc 传入采集到的输入信号数据(实部+虚部形式),同时 FFT 变换后的数据,也按顺序存放在 pSrc 里面,pSrc 必须大于等于 2 倍 fftLen 长度。另外,S 结构体指针参数是先由 arm_cfft_radix4_init_f32 函数设置好,然后传入该函数的。
第三个函数 arm_cmplx_mag_f32 用于计算复数模值,可以对 FFT 变换后的结果数据,执行取模操作。pSrc 为复数输入数组(大小为 2*numSamples)指针,指向 FFT 变换后的结果;pDst为输出数组(大小为 numSamples)指针,存储取模后的值;numSamples 就是总共有多少个数据需要取模。
通过这三个函数,我们便可以完成 FFT 计算,求出模值后便可以求出幅值、相位,知道采样率和FFT长度就可求出频率。
fft.c 代码
#include "arm_math.h"
#include "common.h"
#include "fft.h"
arm_cfft_radix4_instance_f32 scfft;
void FFTx4_init(u8 ifftFlag,u8 bitReverseFlag)
arm_cfft_radix4_init_f32(&scfft,length,ifftFlag,bitReverseFlag);
void cFFTx4(float * pSrc)
arm_cfft_radix4_f32(&scfft,pSrc);
void cmplxFFTx4(float * pSrc,float * pDst)
arm_cmplx_mag_f32(pSrc,pDst,length);
void all_result_x4(float * pSrc,float * Amp,float * rate,float * Phase,u32 Fs)
float pDst[length];
u32 i;
arm_cfft_radix4_f32(&scfft,pSrc);
arm_cmplx_mag_f32(pSrc,pDst,length);
for(i=0;i<length;i++)
if(i==0) Amp[0]=pDst[0]/length;
else Amp[i]=pDst[i]*2/length;
rate[i]=Fs/length*i;
Phase[i]=atan2(pSrc[2*i+1], pSrc[2*i]);
fft.h 代码
#ifndef _FFT_H
#define _FFT_H
#include "arm_math.h"
#include "common.h"
#define length 1024
void FFTx4_init(u8 ifftFlag,u8 bitReverseFlag);
void cFFTx4(float * pSrc);
void cmplxFFTx4(float * pSrc,float * pDst);
void all_result_x4(float * pSrc,float * Amp,float * rate,float * Phase,u32 Fs);
#endif
main.c 代码
#include "common.h"
#include "key.h"
#include "fft.h"
#include "usart3.h"
float input[length*2];
float Amp[length];
float rate[length];
float Phase[length];
int main(void)
u16 i;
NVIC_PriorityGroupConfig(NVIC_PriorityGroup_2);
delay_init();
KEY_Init();
uart3_init(9600);
FFTx4_init(0,1);
for(i=0;i<length;i++)
input[i*2]=100+10*arm_sin_f32(2*PI*i/length)+30*arm_sin_f32(2*PI*i*4/length)+50*arm_cos_f32(2*PI*i*8/length);
input[2*i+1]=0;
while(1)
key_scan(0);
if(keydown_data==KEY0_DATA)
all_result_x4(input, Amp, rate, Phase,1024);
printf("A: F; P\n");
for(i=0;i<length;i++)
printf("%.2f: %.2f: %.2f\n",Amp[i],rate[i],Phase[i]);
delay_ms(5);
测试结果分析
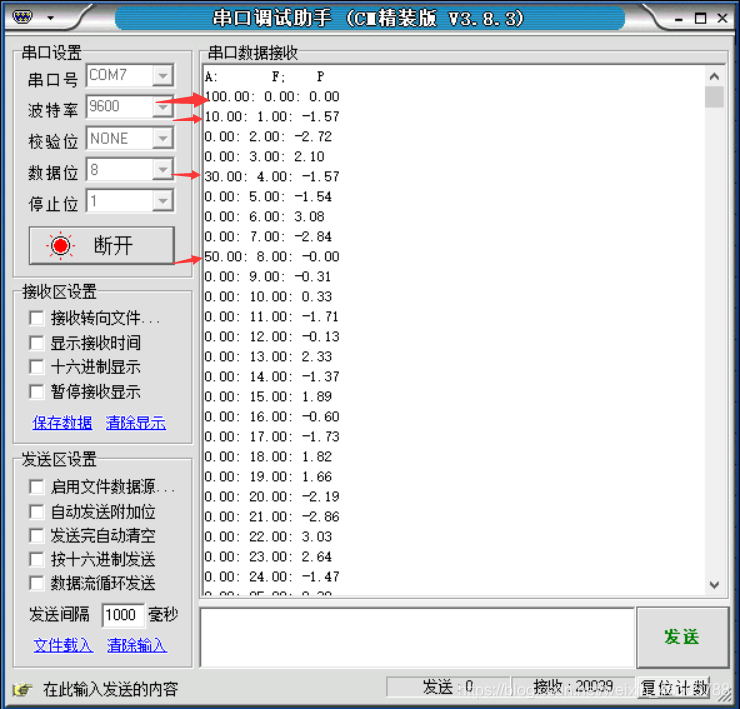
由于 FFT 变换后的结果具有对称性,所以,实际上有用的数据,只有前半部分,后半部分和前半部分是对称关系,比如 第2个点和 最后一个点,5 和 1021,9和 1017 等,就是对称关系,因此我们只需要分析前半部分数据即可。这样,就只有第 1、2、5、9 这四个点幅值比较大,其他点的幅值几乎都是0,重点分析。
采样频率为 1024Hz,那么总共采集 1024 个点,频率分辨率就是 1Hz,对应到频谱上面,两个点之间的间隔就是 1Hz(跟图中第二列完全吻合)。第 1 点,即直流分量,幅值为100,第2、5、9点对应幅值分别为10,30,50,频率分别为1Hz,4Hz,8Hz。因此,可以看出跟上面生成的信号:
100+
10*sin(2*PI*i/1024)+
30*sin(2*PI*i*4/1024)+
50*cos(2*PI*i*8/1024)
几乎完全吻合。
有了上述几个知识点后,我们先来看一下下面的这张图:
这张图是我通过stm32的ADC采集一个1KHZ的方波,然后进行1024个点的FFT得到的,此时的采样率大约为256KHZ,注意:这里的采样率是大约为256KHZ,与256KHZ有较大的偏差,这个偏差造成的后果就是右图的频谱图能量
STM32 属于一个微控制器,自带了各种常用通信接口,比如 USART、I2C、SPI 等,可接非常多的传感器,可以控制很多的设备。现实生活中,我们接触到的很多电器产品都有 STM32 的身影,比如智能手环,微型四轴飞行器,平衡车、移动 POST 机,智能电饭锅,3D 打印机等等。
5. STM32F1移植ST 的DSP官方库
在STMF1上移植ST 的FFT官方库运行一下看一下效果,然而STM32F103毕竟不是STM32F4系列的处理器,对于一般的FFT运算...
FFT可以将一个信号从时域变换到频域,比如一个1VPP的1k的正弦信号,它的时域和频域的示意图如下:
频域为我们观察信号提供了一个新的视角。比如下面是1k和2k信号的叠加。
从时域上看,1k+2k的波形不容易进行处理,也不好猜出来这个波形到底有什么特性(当然这个例子其实还是
系统采用基于ARM-Cortex M4核的STM32F407ZGT6单片机,调用官方DSP库进行4096点FFT运算,后打印出频谱。
本系统中采用了STM32的官方DSP库,DSP库中提供了定点和浮点FF
void arm_cfft_f32(
const arm_cfft_instance_f32 * S, float32_t * p1, uint8_t ifftFlag,
uint8_t bitReverseFlag);
arm_cfft_instance_f32 * S是一个结构体指针这个结构体包含FFT运算的旋转因子和位反转表,就相当于一个常量,我们不用去管它。 f
完整版教程下载地址:http://www.armbbs.cn/forum.php?mod=viewthread&tid=94547
第33章 STM32F407不限制点数FFT实现
本章主要讲解不限制点数FFT的实现。
33.1 初学者重要提示
33.2 不限制点数FFT移植
33.2.1 移植FFT相关文件
33.2.2 添加路径
33.3 不限制点数FFT应用说明
33.3.1 支持的点数范围
33.3.2 函数InitTableFFT
33.3.3 函数...
电子设计大赛已经过去很久了,一直想写一篇关于FFT的文章也没有来得及,现在写一下来记录分享一下。
本篇文章不讲复杂的FFT原理,只讲如何在stm32里面怎么实现FFT
一、FFT是什么,能干啥?
FFT(fast Fourier transform)快速傅里叶变换,把时域信号变换到频域,至于换到频域后能做啥,那就多了
二、先用matlab来认识一下FFT
1.上代码
代码如下:
fs = 1024; %采样频率
NPT = 1024; %样点个数
t=0:1/f



