穿隧（通過勢壘）Tunneling (through a potential barrier)
國立臺灣大學物理學系98級 蔡亦涵

小時候我們也許都有一個經驗，騎腳踏車看到前方有一個小斜坡，好勝心強的我們會想要加足馬力衝上去，如果斜坡不高的話，輕而一舉就過去了，要是斜坡很高，我們在半路就停下來了。

在古典力學裡面，若一個物體的總能量比前方障礙的位能還要小的話，則該物體無法克服位能障礙去到達另一端(圖1)。

圖1 (陳義裕繪)

但是在量子力學的世界裡卻不一定是如此。若物體的尺度小到量子效應明顯的話，即使總能量比位能還低，只要位能不是無限大，也不是無窮寬，的確是有機會穿透過去，我們將它稱為穿隧效應(tunneling effect)。

這聽起來很不可思議，很像是科幻小說或是科幻電影才會出現的情節，而這也就是量子力學令人難以捉摸且迷人的地方。之所以會有上述的情節與可能性，最重要的原因便是：物質粒子在空間中的分布是機率性的，而此機率分布又具有波動的特性。

根據 德布羅意 (de Broglie)提出物質波(matter wave)的概念，認為物質同時具有粒子與波動的特性，而物質波的波長 $$\lambda$$ 滿足等式：

$$\lambda=\displaystyle\frac{h}{p}$$

其中 $$h$$ 為普朗克常數，$$p$$ 為動量。此外，用來計算物質波在空間中出現機率的所謂波函數 $$\Psi(x)$$ 則可由以下的波方程式來描述：

$$\displaystyle -\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}\Psi(x)+V(x)\Psi(x)=E\Psi(x)$$

這是一維的非含時薛丁格方程式(time-independent Schrödinger equation)， $$\hbar$$ 為化約普朗克常數，$$E$$ 是系統總能量。只要位能非無窮大，就一定可以解出波函數的解。即使總能量小於位能，也會有波函數存在，於是粒子就仍有在該區域中出現的機會。

我們也可以用以下更直觀的方式去解釋穿隧效應。先觀察圖2的電腦模擬動畫。

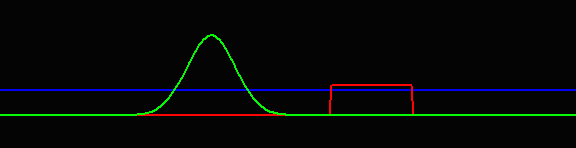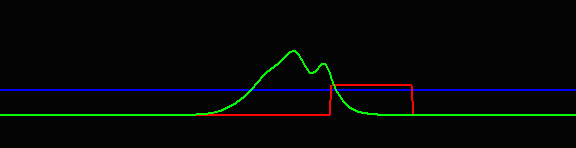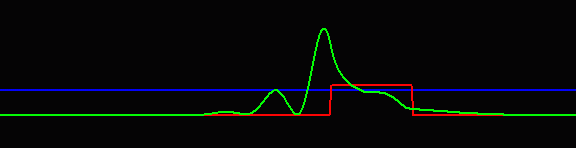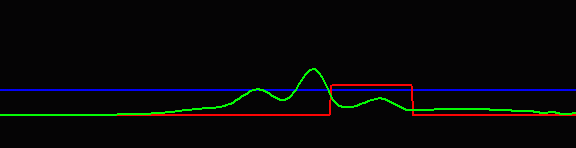
圖2 (陳義裕繪)

假設有一個粒子自左邊入射，它的能量(藍色直線高度)比紅色障礙的最高點之能量稍低，則此粒子在古典物理中是無法超越紅色障礙而跑到右側的。但該粒子遵守的是量子力學，其所對應的物質波(綠色)於進入到紅色障礙區的左側時，一定有部分穿透、部分反射，穿透部分接著就在位能較高的地方進行傳遞，直到當它撞到了紅色障礙的右邊界，此時又會有部分穿透、部分反射，而穿透的部分此後便可繼續朝右方傳播，這就是穿隧。

上面的圖像雖解釋了穿隧發生的可能，但波在位能較高的地方往右傳遞畢竟是十分辛苦的，每多走一步，它能出現在右方的機率就降低許多，要是障礙區域過寬，穿透的比例太低，穿隧效應可能就不那麼顯著了；除此之外，位能障礙越高，要穿透的機會也會越小。

總而言之，理論上只要位能障礙不是無限大、寬度不是無窮寬，都會有穿隧的現象，經過計算，穿隧的比例滿足：

$$T=e^{\displaystyle-\frac{2}{\hbar}\int^a_0\sqrt{2m(V(x)-E)}\mathrm{d}x}$$

其中 $$a$$ 是位能障礙的寬度。由這公式中也可以清楚看到，$$V(x)$$ 越大，或者 $$a$$ 越大，$$T$$ 都會變小，滿足上述的討論。但是公式中也可以清楚看到，有一個數值非常小的 $$\hbar$$ 在那裏，故對巨觀的系統來說，穿隧的機率都趨近於零，所以我們平常幾乎看不到穿隧現象，但如果我們把 $$a$$ 也弄得很小，$$V(x)$$ 不要太大，這樣穿隧效應就越來越顯著。

量子力學的根本假設幾乎就造就穿隧效應的必然，穿隧效應被發現之後，對於科技應用產生很多新的想法，其中掃描穿隧顯微鏡(scanning tunneling microscope, STM)就是一個例子，這個顯微鏡的發明讓我們能對於微觀的尺度做更深入的探究。