一、分解平抛运动的理论依据
通过实验探究,我们得到了这样的结论:平抛运动竖直方向的分运动是自由落体运动,水平方向的分运动是匀速直线运动。
这个结论还可从理论上得到论证。物体以一定初速度
v
0
水平抛出后,物体只受到重力的作用,方向竖直向下,根据牛顿第二定律,物体的加速度方向与所受合外力方向一致,大小为g,方向竖直向下。由于物体是被水平抛出的,在竖直方向的初速度为零,所以平抛运动的竖直分运动就是自由落体运动。而水平方向上物体不受任何外力作用,加速度为零,所以水平方向的分运动是匀速直线运动,速度大小就等于物体抛出时的速度v
0
。这里我们用到了矢量分解的思想。
二、平抛运动的位置随时间变化的规律
如图所示,以物体水平抛出时的位置为坐标原点,以水平抛出的方向为x轴的正方向,竖直向下的方向为y轴的正方向,建立坐标系,并从这一瞬间开始计时。
平抛运动水平方向的分运动为匀速直线运动,故平抛物体的水平坐标随时间变化的规律为x=v
0
t;竖直方向的分运动为自由落体运动,故竖直坐标随时间变化的规律为y=
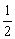
gt
2
。物体的位置可用它的坐标(x,y)来描述,所以以上两式确定了平抛物体在任意时刻t的位置。
三、平抛物体的运动轨迹
从上述两式中消去t,可得y=
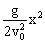
,式中g、v
0
都是与x、y无关的常量,所以
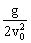
也是常量。这正是初中数学中的抛物线方程y=ax
2
。实际上,二次函数的图象叫作抛物线,就是来源于此。y=
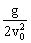
x
2
是平抛运动物体在任意时刻的位置坐标x和y所满足的方程,我们称之为平抛运动的轨迹方程,图象为一顶点在原点且开口向下的抛物线(只有x>0部分)。
四、几个重要结论
1.飞行时间
由于平抛运动在竖直方向的分运动为自由落体运动,有h=
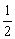
gt
2
,故t=
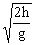
,即平抛物体在空中的飞行时间取决于下落高度h,与初速度v
0
无关。
2.水平射程
由于平抛运动在水平方向的分运动为匀速直线运动,故平抛物体的水平射程即落地点与抛出点间的水平距离x=v
0
t=v
0
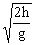
,即水平射程与初速度v
0
和下落高度h有关,与其他因素无关。
3.落地速度
根据平抛运动的两个分运动,可以得到平抛运动的落地速度的大小为v
t
=
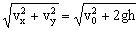
,以θ表示落地速度与x轴正方向之间的夹角,则有tanθ=
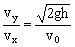
,即落地速度也只与初速度v
0
和下落高度h有关。
4.速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt相同,方向恒为竖直向下。
5.做平抛运动的物体在任意时刻任意位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为
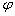
,则有tanθ=2tan
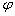
。
6.做平抛运动的物体在任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点。
▍ 来源:综合网络
▍ 编辑:Wordwuli
▍ 声明:如有侵权,请联系删除;若需转载,请注明出处。
▍ 提示:①更多精彩内容,请点击文章标题下方的公众号名称查看;②进入公众号后,发送关键词给我,我会立即回复相关内容给您。
一、分解平抛运动的理论依据通过实验探究,我们得到了这样的结论:平抛运动竖直方向的分运动是自由落体运动,水平方向的分运动是匀速直线运动。这个结论还可从理论上得到论证。物体以一定初速度v0水平抛出后,物体只受到重力的作用,方向竖直向下,根据牛顿第二定律,物体的加速度方向与所受合外力方向一致,大小为g,方向竖直向下。由于物体是被水平抛出的,在竖直方向的初速度为零,所以平抛运动的竖直分运动就是自...
高中
生在
物理
课程中学习
抛物线
运动
。 他们学习了
运动
理论,但是理论与实际
运动
又如何比较? 现实与理论相符吗? 如果不是,什么可以解释差异? 这些问题最好通过进行实验、分析数据、将其与理论进行比较以及观察来回答。
这个应用程序是作为我们为一群
高中
生举办的研讨会的一部分而开发的。 该应用程序允许您分析弹丸
运动
的视频并将其与理论曲线进行比较。 首先拍摄自己扔(扔)球的视频。 然后使用该应用程序导入视频,进行分析和比较。 这是相当不言自明的,但是有一个说明 PDF 描述了如何使用该应用程序。
这个应用程序可以在
物理
研讨会环境中使用,但这个条目的另一个目的是提供关于如何连接理论和实验的想法。
このアプリは,「理论を実験で検证する」というテーマで行った中高生向けワークショップのために作成されたものです。特に,このワークショップでは放物
运动
を取り上げました。実験(动画撮影)から、データの読み込、画像
(function () {
var _$ = function (_this) {
return _this.constructor == jQuery ? _this : $(_this);
// 获取当前时间
function now() {
CSS3动画之
抛物线
今天来说下CSS3动画,目标是让一个方块做
抛物线
运动
。主要用到的CSS3属性有animation,transform,@keyframes,transition等。
GPU硬件加速。
什么是
抛物线
?
以数学
知识
来定义的话,
抛物线
是在
平
面内到定点与定直线的距离相等的点的轨迹叫做
抛物线
。定点就是
抛物线
的焦点,定直线就是
抛物线
的准线。从
物理
上来说的话,
抛物线
就是将一个物体
抛
出去以后,物体
运动
的轨迹。当然,在Unity中我们是从物体的
运动
学的方面来研究的。
在Unity中什么时候需要用到
抛物线
呢?
在Unity中,
抛物线
一般是用来描绘物体的
运动
轨迹,添加拖尾特效或者计算物体的预发射轨迹,用来实现物体的发射瞄准线的。在愤怒的小鸟中,大炮发射、弓箭射击等等游戏中都可以应用到。
抛物线
运动
的种
此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来。同样,这里面也有一些 也可以划归到计算机视觉中去。这都不重要,只要知道有这么个方法,能为自己 所用,或者从中得到灵感,这就够了。
8. Edge Detection 边缘检测也是图像处理中的一个基本任务。...
此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来。同样,这里面也有一些 也可以划归到计算机视觉中去。这都不重要,只要知道有这么个方法,能为自己 所用,或者从中得到灵感,这就够了。
注意:Registration可翻译为“配准”或“匹配”,一般是图像配准,...
此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来。同样,这里面也有一些 也可以划归到计算机视觉中去。这都不重要,只要知道有这么个方法,能为自己 所用,或者从中得到灵感,这就够了。
8. Edge Detection 边缘检测也是图像处理中的一个基本任务。...
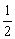 gt
2
。物体的位置可用它的坐标(x,y)来描述,所以以上两式确定了平抛物体在任意时刻t的位置。
三、平抛物体的运动轨迹
从上述两式中消去t,可得y=
gt
2
。物体的位置可用它的坐标(x,y)来描述,所以以上两式确定了平抛物体在任意时刻t的位置。
三、平抛物体的运动轨迹
从上述两式中消去t,可得y=
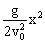 ,式中g、v
0
都是与x、y无关的常量,所以
,式中g、v
0
都是与x、y无关的常量,所以
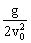 也是常量。这正是初中数学中的抛物线方程y=ax
2
。实际上,二次函数的图象叫作抛物线,就是来源于此。y=
也是常量。这正是初中数学中的抛物线方程y=ax
2
。实际上,二次函数的图象叫作抛物线,就是来源于此。y=
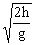 ,即平抛物体在空中的飞行时间取决于下落高度h,与初速度v
0
无关。
2.水平射程
由于平抛运动在水平方向的分运动为匀速直线运动,故平抛物体的水平射程即落地点与抛出点间的水平距离x=v
0
t=v
0
,即平抛物体在空中的飞行时间取决于下落高度h,与初速度v
0
无关。
2.水平射程
由于平抛运动在水平方向的分运动为匀速直线运动,故平抛物体的水平射程即落地点与抛出点间的水平距离x=v
0
t=v
0
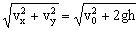 ,以θ表示落地速度与x轴正方向之间的夹角,则有tanθ=
,以θ表示落地速度与x轴正方向之间的夹角,则有tanθ=
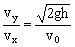 ,即落地速度也只与初速度v
0
和下落高度h有关。
4.速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt相同,方向恒为竖直向下。
5.做平抛运动的物体在任意时刻任意位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为
,即落地速度也只与初速度v
0
和下落高度h有关。
4.速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt相同,方向恒为竖直向下。
5.做平抛运动的物体在任意时刻任意位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为
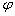 ,则有tanθ=2tan
,则有tanθ=2tan