【电路原理】Chapter 4 电路的若干定理

前情回顾：

本章主要内容：

• 叠加定理
• 替代定理
• 戴维南定理
• 诺顿定理
• 特勒根定理
• 互易定理
• 对偶定理

其中，叠加、戴维南、诺顿、互易四大定理适用于线性电路，替代定理是一个通用定理，对存在唯一解的电路都成立，特勒根定理与基尔霍夫定律一样，对任何集总参数电路普遍适用。

4.1 叠加定理

一般的电路中，含有多个独立电源（电压源和电流源）。叠加定理说明的是在线性电路中由所有各电源共同作用（激励）所产生的各个支路电流（或任意两点间的电压）（响应）与每一电源单独作用时在该支路中产生的电流、电压的关系。

叠加定理的陈述如下：线性电阻电路中，各独立电源(电压源、电流源)共同作用时在任支路中产生的电流（任意两点间的电压），等于各独立电源单独作用时在该支路中产生的电流（该两点间的电压）的代数和。

注意陈述中的“线性电路”，回顾一下前面的知识点：

线性系统：激励（excitation）和响应（response）之间的关系式满足齐次性（homogeneity）和可加性（additivity）的系统。
线性电路（linear circuit）：描述电路的方程为线性方程的电路。

【注意】

1.【单独作用】陈述中的“单独作用”，我们在运用叠加定理时，应当注意到：当电压源不作用时，它的两端必须是短路的，这样オ能保证其两端电压为零；当电流源不作用时，它的两端必须是开路的，这样才能保证其中的电流为零。至于受控电源，因为它们不是独立的电源，在每一独立电源作用时，它们都保持在原有位置。

2.【成立原因】线性电阻电路的叠加定理之所以成立，是因为任何一线性电阻电路，都是由相应的一组线性代数方程来描述的，所以这一定理实质上是关于线性代数方程的叠加定理在线性电阻电路中的表现，由此也就可以看到对一般的线性电阻电路，证明叠加定理的途径。

3.【功率计算】叠加定理只适合于分析电路中的电流、电压，而不能用各电源单独作用时得到的功率叠加来计算电路中的功率。这是因为电阻中的功率是与其中的电流或其两端的电压的平方成正比的（也就是功率的计算是非线性的）。

4.【齐性定理】根据叠加定理容易证明齐性定理：如果线性电阻电路中所有各电压源电压、电流源电流同时增加（或缩减）K倍（K为一实常数），则电路中的各电压、电流均增加（或缩减）为相应的原有的电压、电流的K倍。

最好的也最有代表性的一道例题：

4.2 替代定理

任一线性电阻电路中的一支路两端有电压，其中有电流 i 时，此支路可以用一个电压为 u 的电压源或一个电流为 i 的电流源替代，此电压电源（或电流电源）的参考方向与被替代的支路电压（或电流）的参考方向相同。

下图中，三个电路的工作情形完全相同，即三个电路中对应的支路电流、两点间的电压分别相等。

【注意】

1.【关于非线性】替代定理可推广到非线性电路。（叠加定理不可以哟）

2.【使用条件】在应用替代定理时，要保证替代后的电路解答喉一，否则替代后会出现某些支路的电压或电流是不确定的情况。

同样，一道例题：

4.3 戴维南定理和诺顿定理

戴维南定理和诺顿定理都是关于含有独立电源的线性二端网络的等效电路的定理。二端网络是指仅有两端与外部相联的电路，从这两个端钮中的一端流出的电流与另一端流入的电流相等（KCL）。这样的两个端钮称为一个端口，所以二端网络也称为一端口网络。

回顾第二章曾说，网络内部不含独立电源的二端电阻网络，可以用一个电阻元件来等效。其等效电阻或称输入电阻可用端钮处电压和电流的比值来确定。

当二端网络内部含有独立电源时，其等效电路一般也包含独立电源。

戴维南定理

任一由独立电源和线性电阻组成的二端网络对外部的作用与一电压为 u_{0} 的电压源和电阻 R_{i} 串联的电路等效，其中 u_{0} 是该网络两端断开时的电压；电阻 R_{i} 是该网络中的独立电源不作用时，由二端网络的两端点视入的等效电阻（即入端电阻）。

同样，一道例题：

诺顿定理

戴维南定理是用一个电压源串联电阻等效二端网络，而诺顿定理则是用一个电流源并联电导等效二端网络，其实只是多了一步电压源与电流源的等效变换而已。

使用示范：

注意：

当确定一个含源二端网络的戴维南（诺顿）等效电路时，等效电路中的电压源（电流源）的方向与对应含源二端网络的开路电压（短路电流）的方向有对应关系。

4.4 特勒根定理

相同拓扑的电路： 有相同的结构，即它们的节点、支路分别是一一对应的，而且支路与节点的联接关系也相同的两个电路。（具有相同拓扑的电路，对应支路中的元件可以是不同的）。

特勒根定理： 对两个具有相同拓扑结构的电路A和B，电路A的所有支路中每一支路电压与电路B的对应的支路电流的乘积之和为零。

电压乘电流，看似是功率形式，但由于这个公式中的电压和电流分别来自两个电路，因此它有“似功率”的名称。特勒根定理说明的是似功率的平衡关系。

例子：

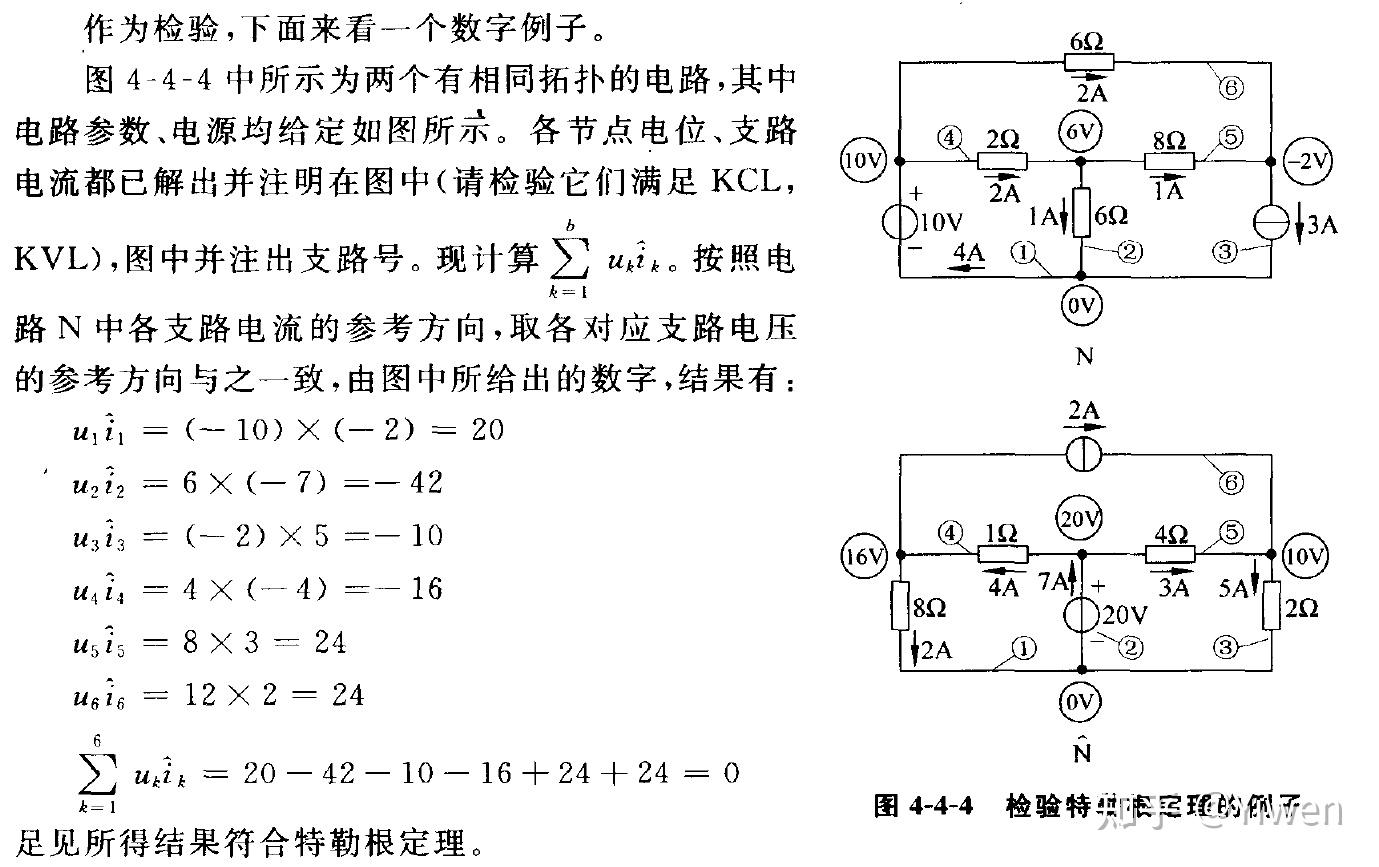
利用特勒根定理可以证明一些电路定理，由特勒根定理可以直接导出电路中的功率平衡定理。

功率平衡定理： 在任一瞬间，任一电路中所有支路所吸收的瞬时功率的代数和为零。

证明很简单，两个电路取的完全一样，然后用特勒根定理就行了。

例题：

4.5 互易定理

对于下图的两个电路：

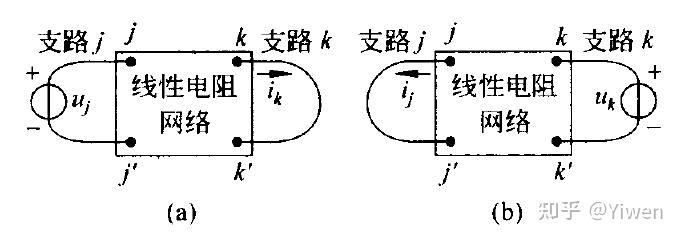
互易定理可以得到：

同样，对于电流源，可以产生互易定理的第二种形式：

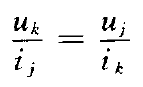
凡是互易定理对之成立的电路就称之为互易电路，或者称有互易性质。

线性电阻电路是互易电路，在后面将可看到：由不随时间变化的线性电阻、电感、电容互感元件组成的电路都是互易电路。含有受控源的电路大多是非互易的，例如电子技术中的各种放大器，就是极明显的非互易电路的例子；但也有含受控电源的互易电路。

许多物理的线性系统（电磁学的，动力学的）都具有互易性质，线性电阻电路只是具有互易性质的许多系统中的一类系统。

4.6 对偶电路与对偶原理

在电路的诸多变量、元件、定律、定理乃至公式间有着某种相似、对应的关系。

（科学就是从未知和“巧合”中寻找规律）

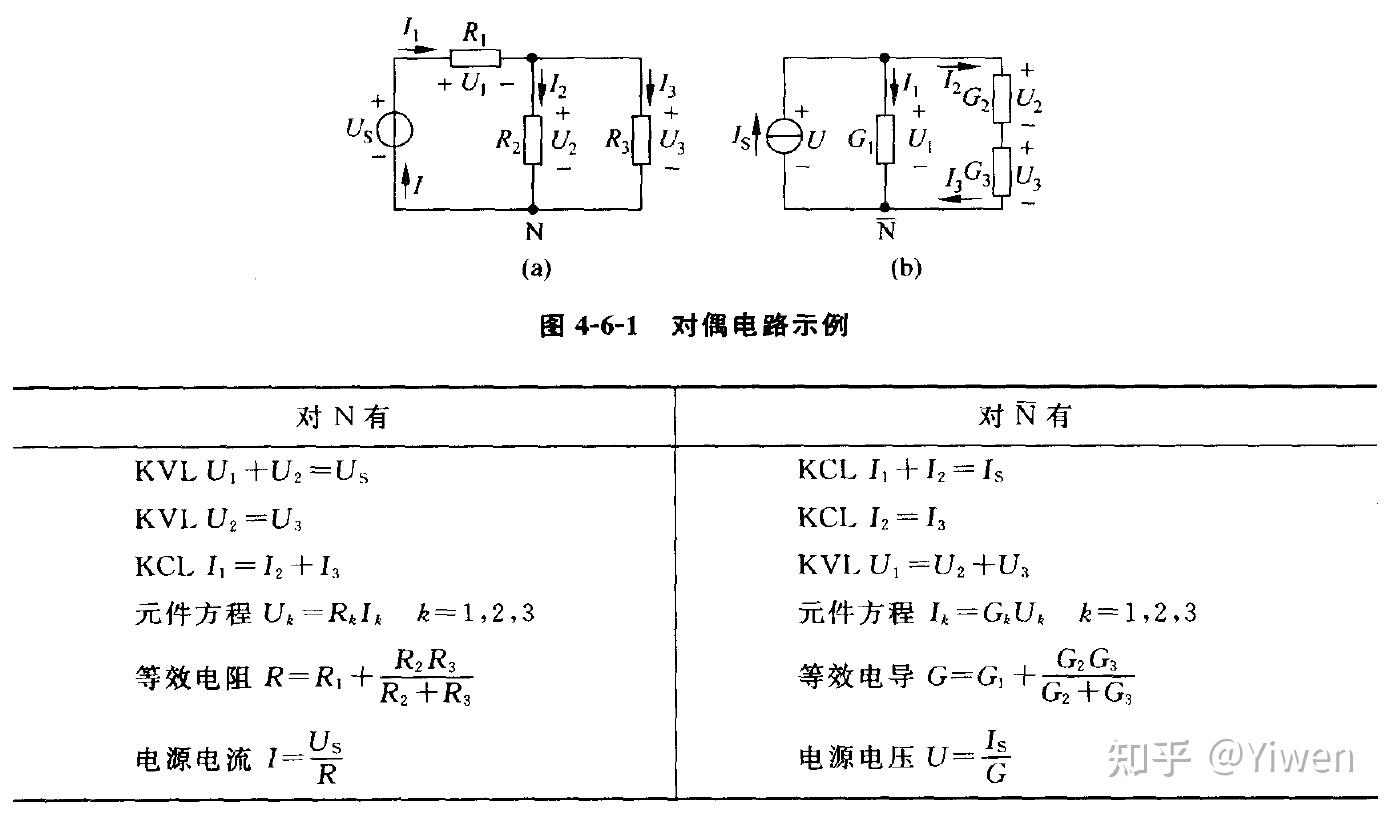
（话说这俩电路也不咋对偶啊，就是公式确实对偶）

对偶电路

设有 b 个支路的电路 N ，满足下列条件的电路 \bar{N} 称为 N 的对偶电路：

（1）将 N 中的KVL方程中的支路电压 u_{j} 换成 i_{j} 便成为对 \bar{N} 成立的KCL方程；

（2）将 N 中以支路电流表示的支路电流 i_{j} 的表达式中的 i_{j} 与 u_{j} 交换，就是 \bar{N} 中的以支路电压 u_{j} 表示的支路电流流 i_{j} 的表达式。

只有平面电路才有对偶电路，非平面电路不可能有对偶电路。

对偶电路找法：

1.看原电路有多少独立网孔，以及外网孔这个非独立网孔。独立网孔将对偶成为独立节点，非独立网孔将对偶成为非独立节点（参考点）。

2.网孔间的公共电阻将对偶成为节点间的电导，网孔共有的电压源对偶成为节点间的电流源，网孔共有的电流源对偶成为节点间的电压源。

对偶原理

任何两个相互对偶的电路 N 和 \bar{N} ，如果对 N 有命题（或陈述）S成立，则将S中的所有各电路变量（电压、电流等）、元件（R，L，C等）、名词（网孔、节点等)）分别以与之对偶的电路变量（电流、电压等）、元件（G，C，L等）、名词（节点、网孔等）替换，所得的对偶命题（或陈述）S对 \bar{N} 成立。

回顾前面所学的定理，诸如电阻的串联与电导的并联、电压电源与电流电源的转换、戴维南定理和诺顿定理等都内涵对偶原理，可以仔细思考一下如何运用的。

下章内容：

待更新中……