【高中数学】如何用计算器解超越方程?
引言:这篇文章我写于2015年10月30日,应该是高二的时候。就想和大家分享一些计算器的使用技巧。这次重新编辑传到知乎。希望对大家有所帮助。
这篇文章想和大家分享一下如何用卡西欧计算器991解一个超越方程(Transcendental Equation) 4^x-x=3 。
我们先来看下百度百科的定义:
超越方程是包含超越函数的方程,也就是方程中有无法用自变数的多项式或开方表示的函数,与超越方程相对的是代数方程。超越方程的求解无法利用代数几何来进行。大部分的超越方程求解没有一般的公式,也很难求得解析解。
当然我们老师给出过一个更为直观的定义:
所谓超越方程,就是超越你能力范围的方程。
原题是这样的,已知 4^x-x=3 的一个根是1,求另外一个根的近似值。
拿到这个方程,就算题目不告诉我们该方程有一根为1,其实大家也是能够看出来的。所以,对于一些简单的超越方程, 首先我们可以猜解 。例如,sinx+x=0,我们可得显然x=0的时候是成立的。当然,大家更普遍的反应,是使用计算器。
在揿计算器之前,首先对原方程做一些简单的移项变形。可以得到两个等价的方程,后面会有用。
4^x=x+3 ①
4^x-x-3=0 ②
通过①式的变形,我们就把原来那个作图相对麻烦的函数,简化成了左边是指数函数,右边是一次函数,这样一个比较简单的形式。

这时候作图可得,这两个函数有两个交点,即原方程有两个根。而且我们可以清楚地看到,另外一个根必然是负的。
对函数图像的研究,有助于我们更快地得到方程的解。而且图像法在求超越方程近似解中非常重要。
要注意的是,交点并不是-3,而且实际画图过程中也做不到那么精确。不过在此,我只是把图像作为求得最后近似解的一个跳板。
至此,原问题变成了:已知 4^x-x=3 的一个根是1,求另外一个负根的值。
这就引出了我由这道题目而想到的三种使用计算器的方法:前两种都是牛顿法的一些小技巧,最后一种是函数零点法。前两种只适用于991及中文版,最后一种适用于所有型号的函数计算器。我将用991中文版作一些简单的示范。
插一个我以前的回答,有助于你们更好地理解下面的内容:
方法一:限定解的范围
如果我们直接用牛顿法,也就是991直接解方程的模式,我们非常有可能得到一个很显然,而且显然是我们不需要的答案:x=1。

顺便我解释一下L-R是什么意思。L就是Left,R就是Right,有些左右逼近的意思。通常情况下我们看到都是L-R=0,简单来说,意为这是一个精确值,如果不为0,就说明x和实际值存在误差。
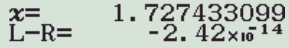
那怎么样才能做到让计算器 强行反馈 给我们一个小于0的解呢?我们可以这样想,有什么值是一定非正的。比如 -x^2 。于是可以把原方程稍作修改,即把x全部替换成 -x^2 。
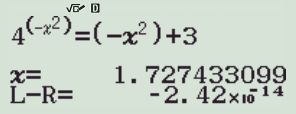
很快可以得到一个x的值,有些细微的误差不用管它。由于做了简单的替换,这并不是我们想要的最终答案。最终答案是 -x^2 。

所以我们得到原方程小于0的根是-2.984。借助函数值域限定解的范围,间接地告诉计算器我们想要的答案是什么,从而得到了我们想要的解。
方法二:设定接近的初始值
上面我们说过,使用牛顿法直接解很有可能得到一个显然的x=1。但是有没有可能直接得到我们想要的-2.984呢?答案是肯定的。举个极端例子:如果我们事先把-2.984赋予x,那么这时候还可能出来1这个答案么。

当然不可能了。

对牛顿法稍有了解的朋友就知道,为什么我们一开始会得到x=1的解,而现在我们可以得到-2.984。牛顿法的结果和初始的位置有很大的关系,通常它只能得到一个离自己比较近的结果。
在没有被赋值的情况下,x默认为0,1相比-2.984更加接近于0。所以我们得到的解是x=1。如果我们赋值-2甚至是-100,因为它们离-2.984更近,所以得到的解就会是x=-2.984。
我们不妨做一个有趣的尝试。我们知道0x=0的解集是x∈R。那如果是计算器会给出怎么样的结果呢?


对,计算器会给出任何值,而且这个值就是你自己赋予他的。你可以理解为你刚开始给计算器一个起点,他就跑到了终点,并给出你一个反馈。
根据牛顿法“离谁进就取谁”的特点,我们可以在不知道的情况下,假设x=-3,因为-2.984更为接近,所以会先得到这个答案,通常这样是比较合理的。
至于如何赋值,我们也有三种方法:
1.按完Shift+Solve之后,计算器会让你赋值

2.按完数字之后按STO(RAGE)

3.最傻的方法,解一下x=-3这个方程

最后插一句,不要认为赋值是一个很鸡肋的功能。当你面临着一个反复要用到黄金分割比 \frac{\sqrt{5}-1}{2} 的多项式,你就会明白它的作用。赋值可以使结果更精准,打起来也更快。
方法三:零点法
虽然耗时耗力,但是零点法比起上述两种奇技淫巧,来得更为基础和普适。而且只要它是个方程,不管方程有多超越,计算器版本有多低,一定可以通过零点法求出个近似解。当然我觉得,零点法不用我说,你们应该都会,只是借这道题目谈一下我的看法。
有一点我们必须认识到,一切方程的根,反映到图像上,最终都是它对应的函数的零点。这时候就用到了②式: 4^x-x-3=0
选择函数/表格/table模式,把4^x-x-3输进去。
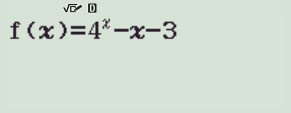
下一步是关键,自变量取什么样的值直接关系到能否快速准确地得到答案。我的习惯是,一般先取-10,10,步长为1。你会发觉1的时候,等于0。毫无疑问x=1是一个根。
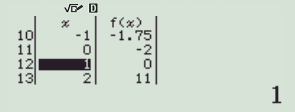
但是并不是每次都这么运气好。你可能得到下图:
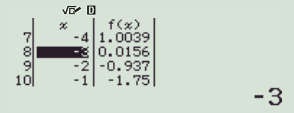
在-3到-2的时候,正负号发生了变化。那说明,一个解在-3到-2之间。其实也就是零点定理:如果 f(a)·f(b)<0 ,那么[a,b]这个区间里是至少有一个零点的。
接下来继续缩小范围,要把步长缩小十倍。

可以得到-3到-2.9之间发生了符号的改变。之后以此类推得到更逼近的解。

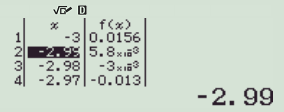
要注意两点:
1. 取值要多但避免溢出。 991中文版是30个,以前的版本是20个。按规律取值可以避免数值数量溢出。
2. 整理后再使用零点法 。如果直接按照原方程。把函数看作4^x-x,然后去寻找靠近3的值虽然可行,但是没有正负变号来得直观,找零点的速度也就慢了。
以上,就是由这个方程衍生出的一些计算器使用小技巧,希望能对好好看过的各位有所帮助。计算器是天使和魔鬼,归根到底取决于你怎么用它。




