不对称三相电路分析有哪些特点和方法?
10 个回答
谢
@伤痕的天空邀。
这个问题让我比较惭愧的。因为当时学得时候也不怎么理解其中的原理,只是会用里面的方法去计算罢了。分析尤其是当问我什么是 对称分量法 的时候,我更是汗颜。
出来实习之后,就更加少手算短路电流了,基本都是用软件算,不过后来想想,软件也是人设定的,终究还是要明白不对称短路计算的原理为好,遂翻起旧书,温习一篇。
下面是我对不对称短路电流计算的见解,不当之处,请指正,谢谢!
------------------------------------------------------------------------------------------------------------------------------------------
补充:负荷不对称和电源不对称在对称分量法眼里都是一个原理的(然后,对称分量法早已看透一切),不管多么复杂或者是负荷,电源如何不对称,利用对称分量法分解后得到的就是简单的电路模型,通过基尔霍夫定律就能分析出来了。
可参考:
何仰赞,温增银《电力系统分析》华中科技大学出版社,第三版,上册
当然,想装逼点可以参考:
电力工业部电力规划设计总院《电力系统设计手册》中国电力出版社
分割线----------------------------------------------------------------------------------------------------------------------------------
1、 首先,我们要明白什么是对称电路,什么是不对称电路 。
简单地说就是系统中三相电abc相三相电流大小相等、相位依次相差120°。电压亦是如此。
(因为用对称分量法分析,对于电流和电压都是一样的原理,所以我只用电流作为例子分析)
对称三相电流如下图:
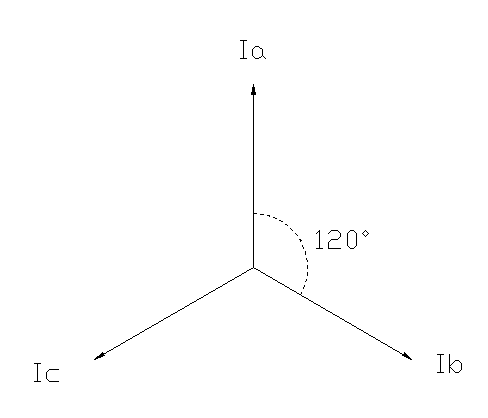
(注:这些都是相量,应该在其顶部有一个点的,但因为画图工具不方便,所以我的就不画出来)
那么不对称电路就是其电流、电压三相的关系不符合上面的条件,即大小不等或者相位差不是120°
如下图:
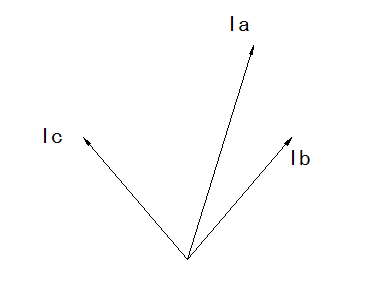
2、然后,我们要从一个数学领域中得到一个思维过渡,也是 对称分量法的原理 。
我们都很熟悉平面直角坐标系:

对于任意一个向量都可以将其分解为X轴分量和Y轴分量!例如上面的Y向量,可以把他分解为Yx、Yy分量。
那么,这个坐标轴,是我们人为定义的,我们可以定义X轴和Y轴是垂直的,也可以是不垂直的,我们可以定义两根轴,也可以定义三根轴。
所以, 对称分量法的原理就是,人为自定义一个三根轴的坐标系:
例如对于a相,我们把这个坐标系定义成下面这个样子:
三根轴:零序轴(a(0)、正序轴a(1)、负序轴a(2)):
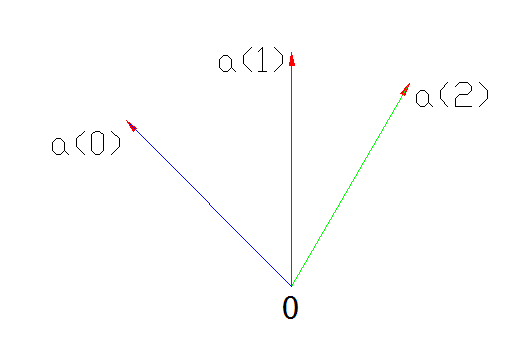
然后,把 刚刚那组不对称电流 中的a相电流放到上面坐标轴来分解:
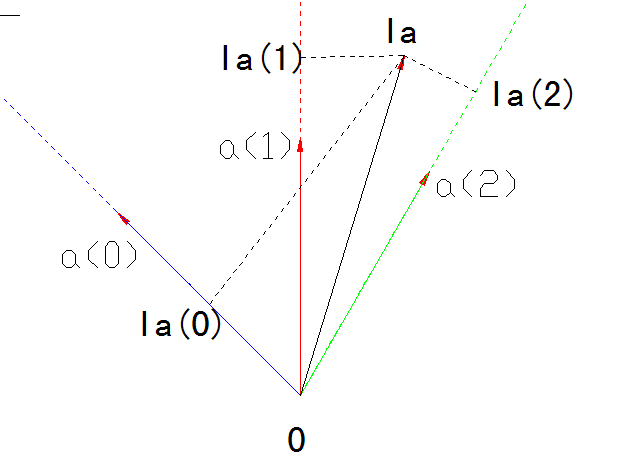
这样,我们就可以把刚刚那组不对称电流中的a相电流Ia分解成其正序分量Ia(1)、负序分量Ia(2)和零序分量Ia(0)。
同样的道理,我们可以这样定义另外两个坐标轴把 上述那组 不对称电流的b相和c相的电流分解掉:
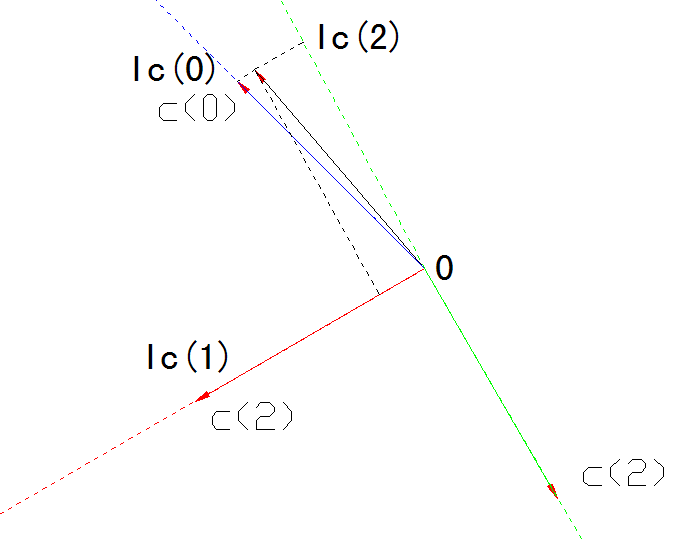
那么,不对称电流中的c相电流Ic分解成其正序分量Ic(1)、负序分量Ic(2)和零序分量Ic(0)
(b相的就不画了,主要是懂原理接好了。)
通过刚刚的坐标轴分解,我们是否得到了每相电流的各序分量?
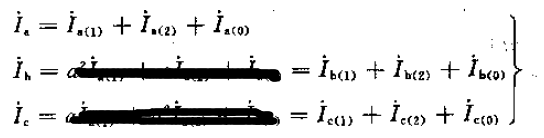
式2-1
以上,便是如何如何利用对称分量法去分解一组不对称分量的过程。
当然,各相坐标轴之间还是有一定关系的 :
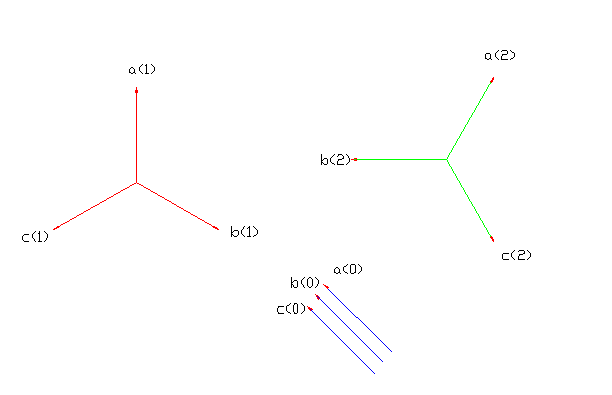
如上图,把各相各序的坐标轴组合,得到的是上面关系,即各相正序要大小相等,相位差120°,且abc相顺时针,负序大小相等,abc相逆时针顺序,零序大小相等,abc相同相位。
至于为什么要这么安排,其实,就是为了分析方便,就好比为什么平面直角坐标系x轴和y轴要垂直
当我们再引入运算子:
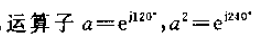
可以得到这样的关系:
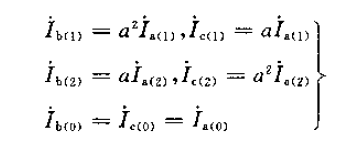
再代入式2-1得:
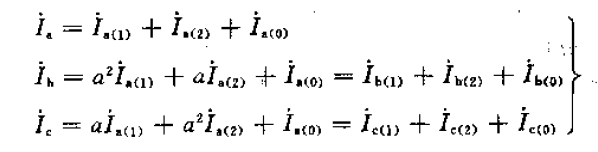
3、
好了,分析完了什么是对称分量法的原理, 下面就用一个例子来分析对称分量法的应用!
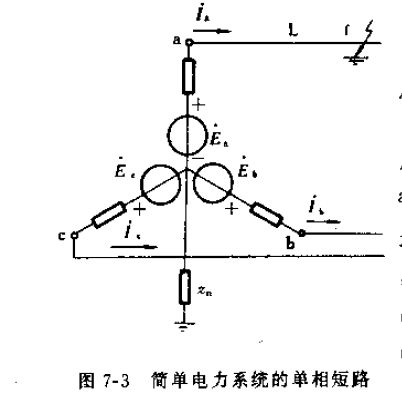
a相发生接地短路,也就是不对称短路。
我们知道,单相对地短路的边界关系为:
Vfa=0,Ifb=Ifc=0;
将上图等效为:
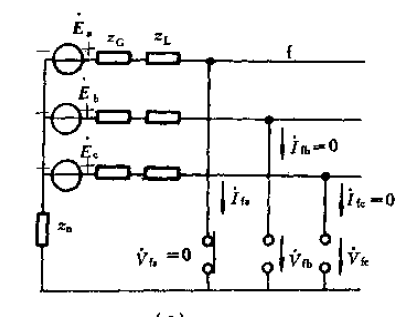
利用上面学到的对称分量法,把Vfa,Vfb.Vfc分解为其各自的正序、负序和零序,如下图:
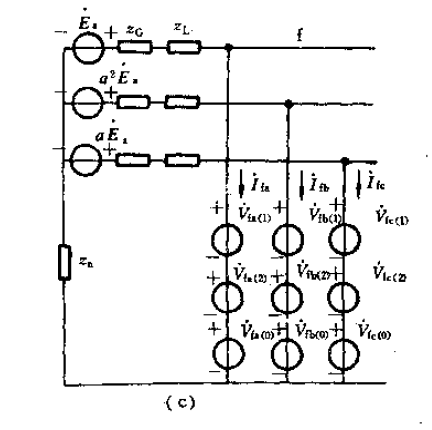
那么,从中取出其正序网络为:
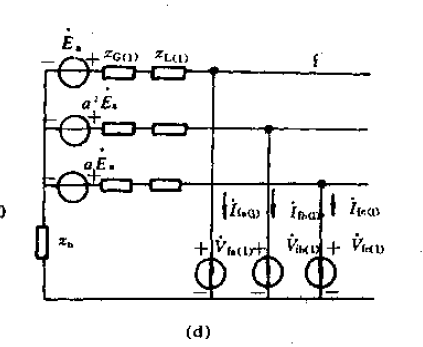
利用基尔霍夫定律(KVL),可以得到:
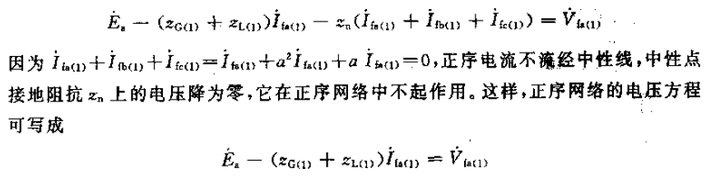
同理,从中取出负序网络,为:
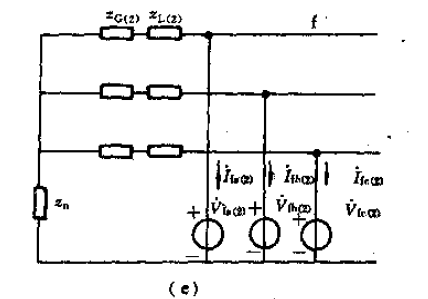
利用基尔霍夫定律得:

零序网络:
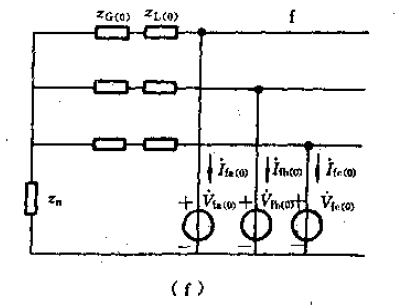
利用基尔霍夫定律得:
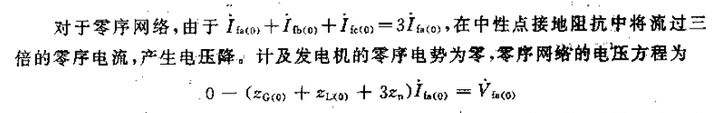
回到刚刚提到的 边界条件 ,又可以得到:
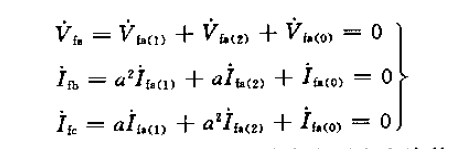
那么,由上面的六个方程式,可以解出短路点的电压、电流了!
以上!!!!
--------------------------------------------------------------------------------------------------------------------------------
参考文献:
何仰赞,温增银《电力系统分析》华中科技大学出版社,第三版
电力工业部电力规划设计总院《电力系统设计手册》中国电力出版社
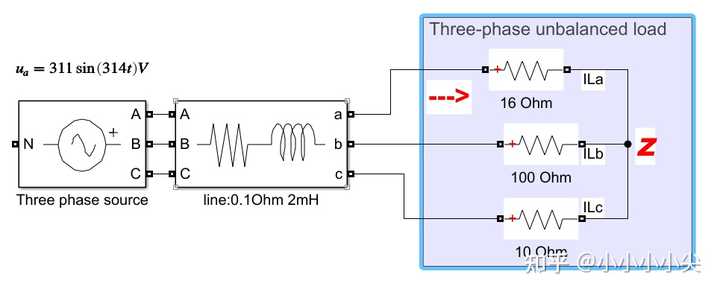
There are plenty of literature or article discussing how to deal with asymmetric fault in power system using symmetrical component method. However, the application of symmetrical component method under unbalanced load condition is rarely mentioned in literature. In this article, the symmetric component method is used to solve this problem. An example is given to illustrate the principle.
U_{LA}=U_{LA}^++U_{LA}^-+U_{L0}\\ U_{LB}=U_{LB}^++U_{LB}^-+U_{L0}\\ U_{LC}=U_{LC}^++U_{LC}^-+U_{L0}
Positive sequence equivalent:
U_A^+=(R+j\omega L)I_{LA}^++U_{LA}^+
Negative sequence equivalent:
0=(R+j\omega L)I_{LA}^-+U_{LA}^-
Zero sequence equivalent: No zero sequence current path!
Boundary conditions:
U_{LA}=Z_AI_{LA}\\ U_{LB}=Z_BI_{LB}\\ U_{LC}=Z_CI_{LC}\\
U_{LA}^++U_{LA}^-+U_{L0}=Z_A(I_{LA}^++I_{LA}^-)\\ \alpha^2U_{LA}^++\alpha U_{LA}^-+U_{L0}=Z_B(\alpha^2I_{LA}^++\alpha I_{LA}^-)\\ \alpha U_{LA}^++\alpha^2U_{LA}^-+U_{L0}=Z_C(\alpha I_{LA}^++\alpha^2I_{LA}^-)\\
U_{LA}^++(R+j\omega L)I_{LA}^+=U_A^+\\ U_{LA}^-+(R+j\omega L)I_{LA}^-=0\\ U_{LA}^++U_{LA}^-+U_{L0}-Z_A(I_{LA}^++I_{LA}^-)=0\\ \alpha^2U_{LA}^++\alpha U_{LA}^-+U_{L0}-Z_B(\alpha^2I_{LA}^++\alpha I_{LA}^-)=0\\ \alpha U_{LA}^++\alpha^2U_{LA}^-+U_{L0}-Z_C(\alpha I_{LA}^++\alpha^2I_{LA}^-)=0\\
MATLAB SOLUTION:
w=2*pi*50;
a=1*exp(j*2*pi/3);
z=0.1+j*w*2e-3;
ua=311;
za=16;zb=100;zc=10;
A=[1 0 0 z 0;
0 1 0 0 z;