快速傅立叶变换（Fast Fourier Transform）笔记

3 年前 · 来自专栏统计力学和量子动力学专题

薛定豆

Chemical Physics

快速傅立叶变换在信号处理和物理化学的诸多领域（如超快光谱）有着非常重要的地位，下面简单记录一下其中的要点。

参考书有：E. Brigham, Fast Fourier Transform and Its Applications

1. 连续傅立叶变换（Continuous Fourier Transform）

对于时域连续函数 x(t) ，它的傅立叶正变换（FT）定义为

\mathcal F[ x(t)] = X(\omega) = \int_{-\infty}^\infty x(t) e^{-i\omega t}dt （用角频率 \omega 表示) 或者 \mathcal F[ x(t)] = X(f) = \int_{-\infty}^\infty x(t) e^{-i2\pi f t}dt （用频率 f 表示, \omega = 2\pi f )

傅立叶逆变换（inverse FT）定义为

\mathcal F ^{-1}[ X(\omega)] = x(t) = \frac{1}{2\pi} \int_{-\infty}^\infty X(\omega) e^{+i\omega t}d\omega = \frac{1}{2\pi} \int_{-\infty}^\infty X(f) e^{+i2\pi f t}df

2. 离散傅立叶变换（Discrete Fourier Transform, DFT）

如果有等时间间距 \Delta t 的时域信号N个： x[n],\text{where } n=0,\ldots,N-1 ,它的离散傅立叶变换（DFT）定义为

\mathcal F[x[n]]=X(e^{i\omega}) = X[k] = \sum_{n=0}^{N-1}x[n] e^{-i\frac{2\pi}{N}nk}, \;\;(k=0,\ldots,N-1)\\

这里 \omega = \frac{2\pi}{N} k . 相应的逆变换定义为

\mathcal F^{-1}[X[k]]=X(e^{i\omega}) = x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k] e^{i\frac{2\pi}{N}nk}, \;\;(n=0,\ldots,N-1)\\

3. 快速傅立叶变换（Fast Fourier Transform, FFT）

快速傅立叶变换FFT是一种更加高效的计算离散傅立叶变换的算法，有着 O(N log_2 N) 的计算复杂度，比原始的DFT O(N^2) 计算复杂度有更好的可扩展性。Cooley-Tuckey算法是一种常见的FFT实现方式，但是需要限制输入数据点数 N=2^m （2的乘方）形式。

如果你的数据数量不是2的几次幂，可以通过在后面加0（zero padding）的方式凑成下一个2的乘方个数据，添加的0不会影响频域谱，只会增加表观数据密度，即多出来的频域点其实是有效数据的线性内插值 Linear interpolation，如下图所示：

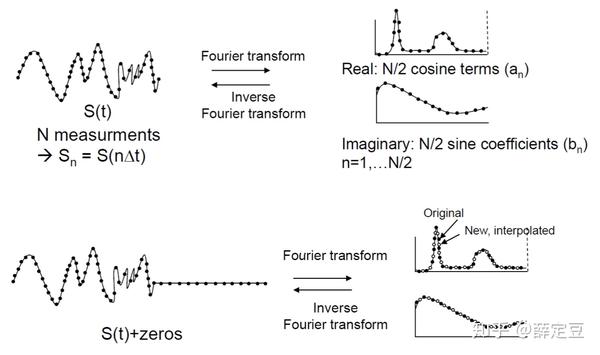
对于zero padding证明如下：

如果记原始时域信号的离散傅立叶变换为 F(e^{i\omega}) = \sum_{n=0}^{M-1} f[n]e^{-1\omega n} ，其中时域数据数为 M . 我们添加0到后面，记zero padding的信号为 g[n]=f[n]+zeros, (M\le n \le N-1) , N 是2的乘方。所以 g[n], (n=0,\ldots,N-1) 的离散傅立叶变换为 G(e^{i\omega}) = \sum_{n=0}^{N-1} g[n]e^{-i\omega n}= \sum_{n=0}^{M-1} f[n]e^{-i\omega n}+ \sum_{n=M}^{N-1} 0\times e^{-i\omega n}=F(e^{i\omega}) \qquad \square\\

离散傅立叶变换得到的频域信号是以 \Delta f=\frac{1}{N\Delta t} 为间距的，最大频率称做Nyquist频率，即为 f_{Nyquist}=f_{max} = \frac{1}{2\Delta t} ，它只跟时域信号的步长有关。经过FFT变换的频域信号对应的下列频率

\begin{align} f=\frac{\omega}{2\pi} = & 0, \Delta f, 2\Delta f, \ldots, (N/2-1)\Delta f,\\ & \pm (N/2)\Delta f, -(N/2-1)\Delta f, -(N/2-2)\Delta f, \ldots, -\Delta f. \end{align}\\

也就是说，前一半是正的频率，后一半是负的频率，中间点是正负最大频率。一般画图的话，需要把后一半挪到前面。

4. 时间移位 Time shifting

如果输入的时域数据第一个数据对应的不是时间零点而是 t_0 ，那么直接得到的频域信号为

\mathcal F[ x(t-t_0)] = \int_{-\infty}^\infty x(t-t_0) e^{-i2\pi f t}dt= \int_{-\infty}^\infty x(t') e^{-i2\pi f (t'+t_0)}dt= \mathcal F[ x(t)]\cdot e^{-i2\pi f t_0}\\

所以，要想得到真实数据的傅立叶变换，需要乘以 e^{i2\pi f t_0} 因子，也就是

\mathcal F[x(t)] = \mathcal F[x(t-t_0)] \cdot e^{i2\pi f t_0}\\

离散情形为 \mathcal F[x[n]] = \mathcal F[x[n-n_0]] \cdot e^{i\frac{2\pi}{N} n_0k}\\

下图是高斯函数 x(t) = e^{-at^2},\; a=32 没有经过时间移位的傅立叶变换 \mathcal F[e^{-a(t-t_0)^2}] ：

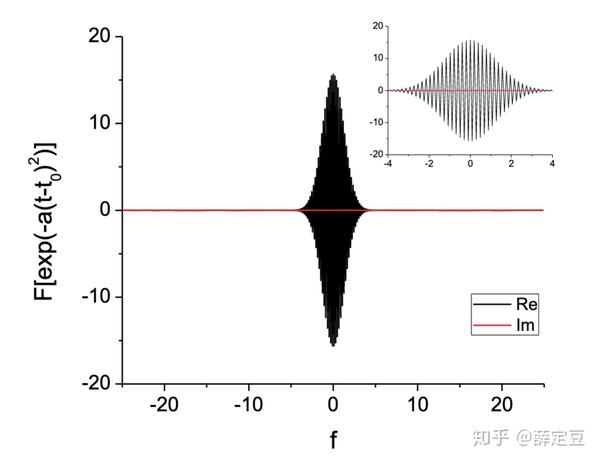
下图是高斯函数 x(t) = e^{-at^2},\; a=32 经过时间移位的傅立叶变换 \mathcal F[e^{-at^2}] ：

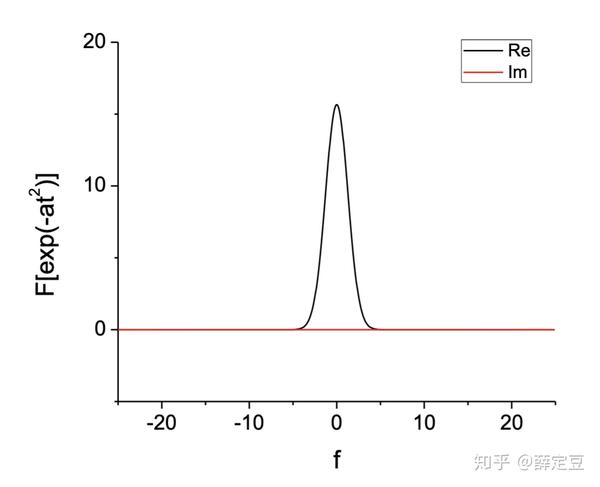
5. FFT 的 C程序

其中m是N=2^m的指数，x和y是实部和虚部

void FFT(int dir, int m, double *x, double *y)
  This code computes an in-place complex-to-complex FFT Written by Paul Bourke
  x and y are the real and imaginary arrays of N=2^m points.
  dir =  1 gives forward transform
  dir = -1 gives reverse transform  
  Formula: forward
         \           - i 2 pi k n / N
  X(n) =  >   x(k) e                       = forward transform
         /                                    n=0..N-1
  Formula: reverse
            1  \           i 2 pi k n / N
  X(n) =  ---  >   x(k) e                  = forward transform
            N  /                               n=0..N-1
    int n,i,i1,j,k,i2,l,l1,l2;
    double c1,c2,tx,ty,t1,t2,u1,u2,z;
    // Calculate the number of points
    n = 1;
    for (i=0;i<m;i++)
        n *= 2;
    // Do the bit reversal
    i2 = n >> 1; //i2 = (010 ...0)_2,second highest bit of n=(100 ...0)_2
    j = 0; //reversely bit accumulater from the second highest bit, i2.
    for (i=0;i<n-1;i++) {
        if (i < j) {
            tx = x[i]; //swap(i,j)
            ty = y[i];
            x[i] = x[j];
            y[i] = y[j];
            x[j] = tx;
            y[j] = ty;
        //to find the highest non-one bit, k, from the second highest bit
        k = i2;
        while (k <= j) {
            j -= k;
            k >>= 1;
        j += k; //add 1 reversly
    // Compute the Radix-2 FFT: Cooley-Tukey Algorithm
    c1 = -1.0; // c1+i*c2 = -1 = c^(i 2Pi/2) = W_2, def W_N^j = e^(i 2j*Pi/N)
    c2 = 0.0;
    l2 = 1;
    for (l=0;l<m;l++) {
        l1 = l2;
        l2 <<= 1;
        u1 = 1.0;
        u2 = 0.0;
        for (j=0;j<l1;j++) {
            for (i=j;i<n;i+=l2) {
                //Butterfly calculation of x,y[i] and x,y[i1]:
                //t1+i*t2 =(u1+i*u2)(x[i1]+i*y[i2]) where u1+i*u2=W_N^j=e^(i 2j*Pi/N)
                i1 = i + l1;
                t1 = u1 * x[i1] - u2 * y[i1];
                t2 = u1 * y[i1] + u2 * x[i1];
                x[i1] = x[i] - t1;
                y[i1] = y[i] - t2;
                x[i] += t1;
                y[i] += t2;
            // i1+i*u2 *= c1+i*c2, or W_N
            z =  u1 * c1 - u2 * c2;
            u2 = u1 * c2 + u2 * c1;
            u1 = z;
        //c1+i*c2 = sqrt(c1+i*c2) eg. W_2 --> W_4 ...
        c2 = sqrt((1.0 - c1) / 2.0);
        if (dir == 1)
            c2 = -c2;
        c1 = sqrt((1.0 + c1) / 2.0);
    // Scaling for inverse transform
    if (dir == -1) {
        for (i=0;i<n;i++) {
            x[i] /= n;