• lfilter 可以用于 在线 数据的滤波
• 之前笔记的 filtfilt 用于离线数据，不会有相位差
  （可参考之前笔记： Butterworth Filter 巴特沃斯滤波器的python代码应用 ）

# initial filter param  
def init_filter(self, order, cutoff, fs):
	wn = 2.0*cutoff/fs
	self._b, self._a = sig.butter(order, wn, 'lowpass', analog = False)
	self._dss = sig.lfilter_zi(self._b, self._a)
def lfilter_filter(self, f_x, f_y, f_z):
    f = [f_x, f_y, f_z]
    res = [0,0,0]
    for i in range (0,3):
        res[i], self._dss[i] = sig.lfilter(self._b, self._a, [f[i]], zi=self._dss[i])
    return res[0][0], res[1][0], res[2][0]    
init_filter(order=3, cutoff=4, fs=100)
 
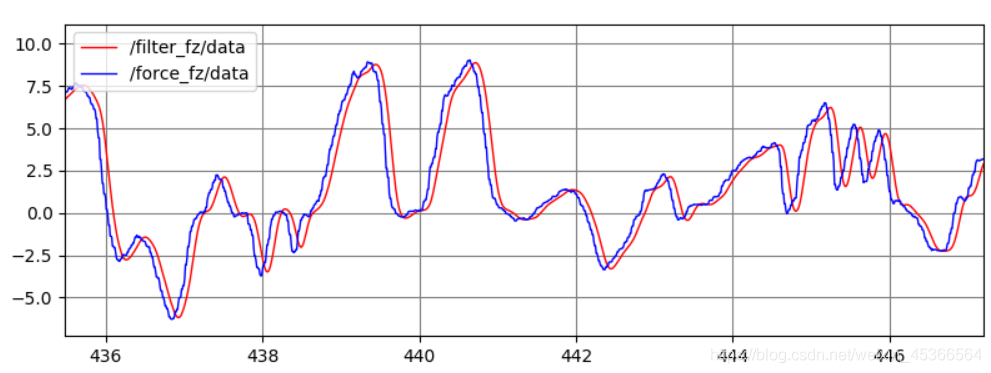
 init_filter(order=3, cutoff=6, fs=100)
 
 
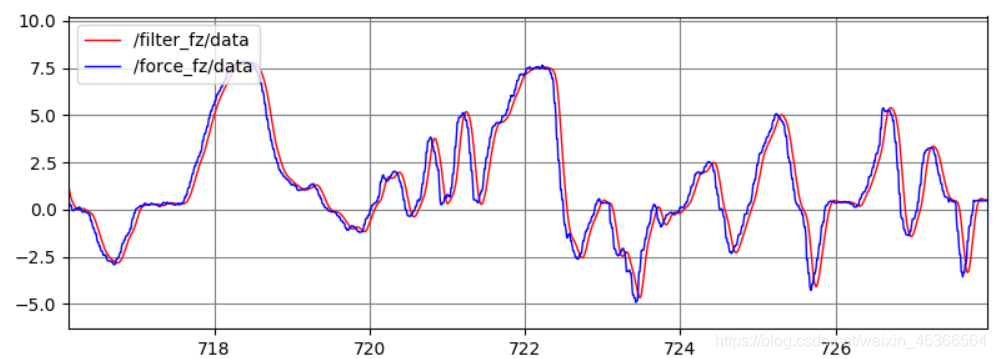
一些文字：在scipy.signal中应用过滤器：使用lfilter还是filtfilt？
 一些代码：scipy中 filtfilt和lfilter 区别
                    lfilter可以在线滤波使用# initial filter param  def init_filter(self, order, cutoff, fs):	wn = 2.0*cutoff/fs	self._b, self._a = sig.butter(order, wn, 'lowpass', analog = False)	self._dss = sig.lfilter_zi(self._b, self._a)Plotinit_filter(order=3, cutoff=4, f
				
filter与filtfilt的区别
转载自：https://blog.csdn.net/Galaxy_Robot/article/details/106976165
经过filter滤波的信号比原始信号明显有延迟，而经过filtfilt滤波后的信号几乎没有延迟
f1=10;
f2=20;
f3=30;
Fs=150;
t=0:1/Fs:1;
y1=5*sin(2*pi*f1*t)+10*sin(2*pi*f2*t)+8*sin(2*pi*f3*t);
subplot(3,1,1);plot(y1);
				
filter函数 与filtfilt函数的效果区别
filter滤波器称为一维数字滤波器。filtfilt滤波器称为零相位数字滤波。其滤波算法是基于filter而来的。只是filtfilt实现了零相位。其基本实现过程为先让信号用filter滤波，再将信号时域反转再次通过filter滤波，这样两次滤波后相位实现了零相位。filter滤波有明显的延迟，filtfilt滤波延时比filter小很多。分析如下（程序参见matlab脚本，完整程序下载链接）：
（1）设置三种频率(10Hz,20Hz,30Hz)构成的信
1、滤波器的基本概念 
  滤波器的功能是允许某一部分频率的信号顺利通过，而另外一部分频率的信号受到较大的抑制难以通过。实际上可以看作是一个选频电路。
  滤波器中，信号能够通过的频率范围，称为通频带或者通带；
  滤波器中，信号受到较大抑制疯狂衰减的频率范围称为阻带；
  滤波器中，通带和阻带之间的分界频率称为截止频率；
  实际滤波器的通带和阻带之间存在一定频率范围的过渡带。
1、滤波器的频率适用范围 
  滤波器的应用频率范围较宽，从不到1hz到微波段的高频均可以；根据滤波频率的中心频
				
Python高通滤波器是一种信号处理技术，它可以去除信号中低频成分，只保留高频信号。高通滤波器可以通过不同的滤波器设计方法来实现，例如Butterworth滤波器、Chebyshev Type I和Type II、Elliptic滤波器等。
在Python中，常用的高通滤波器是Butterworth滤波器。这个滤波器可以使用SciPy库中的signal模块实现。具体实现过程包括以下几个步骤：
1. 导入必要的库。首先需要导入NumPy和SciPy库。
2. 定义滤波器参数。这里需要定义高通滤波器的截止频率和滤波器的阶数。截止频率是指信号中需要去除的低频成分的频率。阶数是指滤波器的复杂度，影响滤波器的陡峭程度和穿透度。
3. 调用Butterworth高通滤波器函数。使用signal模块中的butter函数可以创建一个Butterworth高通滤波器对象。
4. 应用滤波器。使用lfilter函数可以将滤波器应用到信号。
总的来说，高通滤波器是一种非常重要的信号处理技术，可以用于去除信号中的低频噪声或不想要的低频成分。通过Python和SciPy库，我们可以很方便地实现高通滤波器的设计和应用。