热力学哟！统计物理啊！（学习札记）

我们也好奇热力学里的 独立变量 是什么？有几个？下图是让我瞬间明白的讲解：

书中所说的“变数”我理解成变量或者参量（汪志诚的《热力学·统计物理》用了“参量”），体积是 几何参量 ，压强是 力学参量 。

• 如果研究对象是 多种气体 ，就得引入化学组分（各种气体分压）——属于 化学参量 。
• 如果研究对象有 电磁现象 ，以上三种参量还是不完全，还得引入 电磁参量 ，如电场强度、磁场强度等等。

终于完整了！总结起来，在热学上对于一个物体的平衡态需要用四类参量去描写才能完全，这四类是：几何参量，力学参量，电磁参量，化学参量。实际上这些参量并不相互独立，因为参量之间需要满足一定的关系，系统才能达到平衡，它们之间的关系叫做 平衡条件 。平衡条件有四种：（括号里是读者临时想出来的例子，可能不完全恰当）

1. 热平衡条件（温度相等，后面会重点介绍温度的概念，比如热力学第零定律即热平衡定律）
2. 力学平衡条件（吹气球时，气球膨胀以达到力学平衡）
3. 相变平衡条件（水蒸气和水的两相平衡：水蒸气的气压达到饱和蒸汽压时，更严格的定义是两相化学势相等）
4. 化学平衡条件（化学反应的平衡会受很多因素的影响，几何参量、力学参量和电磁参量任意一个变了，化学平衡就被破坏，所以化学参量不是独立变量，它是其他三类参量的函数）

说到这，读者肯定也好奇统计力学的目的是什么？统计方法有两个目标：第一个是推导热力学定律，第二个是推导关于系统的宏观性质的方程。笔者愚见，统计力学是对热力学现象的微观解释。更多关于统计物理的内容可以读 @yubr 的文章，写得很自然

热力学第零定律（引进一个态函数，用温度相等来表征热平衡）

上图通过观察平衡态现象得到的原理，叫热平衡定律，也叫热力学第零定律。

热学中最核心的概念是“温度”与“热量”。历史上定义这些概念都颇费一番周折，我们先来看温度：

温度的直观定义：标记物体冷热程度的物理量称为温度。这个直观定义并没有揭示温度的本质！比如怎么衡量物体的冷热程度？靠人的皮肤感觉吗？

温度的本质：温度是组成物体的大量分子无规则运动剧烈程度的表现。

更多关于温度的讨论可以参考：

在科学史上长期以来这些基本概念是混淆不清的(见赵凯华书第一章第二节关于量热学的历史)。“但是一经辨别清楚， 就使得科学得到飞速的发展。”( 爱因斯坦)。

重构后的热力学根据热力学第零定律证明处于平衡态的系统的态函数——温度的存在：

为明确起见，我们考虑 简单系统—— 只需要体积 V 和压强 p 两个状态参量便可以确定系统的状态。设系统 C 处在热平衡状态，体积为 V_{C} ，压强为 p_{C} ，对于系统 A、B 则用相应的下标 A、B 。如果用 \Leftrightarrow 表示热平衡，那么热平衡定律可以简记如下：

\begin{cases} A\Leftrightarrow C\\ B\Leftrightarrow C \end{cases} \Rightarrow A\Leftrightarrow B

推导：

如果 A\Leftrightarrow C ，即 F_{1}(p_{A},V_{A};p_{C},V_{C})=0\Rightarrow p_{C}=f_{1}(p_{A},V_{A};V_{C})

如果 B\Leftrightarrow C ，即 F_{2}(p_{B},V_{B};p_{C},V_{C})=0\Rightarrow p_{C}=f_{2}(p_{B},V_{B};V_{C})

于是有 f_{1}(p_{A},V_{A};V_{C})=f_{2}(p_{B},V_{B};V_{C})\tag{1}

根据 热力学第零定律 ， F_{3}(p_{A},V_{A};p_{B},V_{B})=0\tag{2}

\begin{cases} f_{1}(p_{A},V_{A};V_{C})=\phi_{1}(p_{A},V_{A})\xi(V_{C})+\eta(V_{C})\\ f_{2}(p_{B},V_{B};V_{C})=\phi_{2}(p_{B},V_{B})\xi(V_{C})+\eta(V_{C}) \end{cases}

联立（1）式，得 \phi_{1}(p_{A},V_{A})=\phi_{2}(p_{B},V_{B})

自然地推广 \phi_{1}(P_{A},V_{A})=\phi_{2}(P_{B},V_{B})=\phi_{3}(P_{C},V_{C})=\vartheta

\vartheta 便是经验温度，这意味着即便有 n 个相互平衡着的系统，那么它们都有共同的数值 \vartheta 来描写这个平衡状态。这就是经验温度的来源。

热平衡定律的意义

1. 给出了温度的概念，即互为热平衡的系统 A、B 各自存在其 数值相等 的一个状态函数 \phi_{1}(p_{A},V_{A}) 和 \phi_{2}(p_{B},V_{B}) ，经验表明，两个物体达到热平衡时具有相同的冷热程度——温度，所以 态函数 \phi(p,V) 就是系统的温度 。
2. 指明了比较温度的方法，为了比较两个物体的温度，可以借助第三者—— 温度计 。

温度的进一步讨论及其统计定义

推荐阅读：《热物理概念——热力学与统计物理学》第2版 Blundell 著 鞠国兴 译 Page33~46

注意

热平衡状态（温度相等——热平衡） \ne 热力学平衡状态（压力相等——力学平衡、温度相等——热平衡、化学势相等——相变平衡）

物态方程

先通过一个例题了解常出现在物态方程表达式中的三个系数，第一次学到这几个系数时我只看了个表面，后来反复咀嚼，发现它们的量纲都是自变量的倒数，拿体胀系数说明一下，体胀系数的含义是，在压强维持不变的条件下，温度升高1K所引起的物体体积的 相对 变化。强调“相对变化”是想让你明白为什么要除以体积V

类似的，压强系数的含义是，在体积维持不变的条件下，温度升高1K所引起的物体压强的 相对 变化。强调“相对变化”是想让你明白为什么这里也要除以压强p

等温压缩系数的含义是，在温度维持不变的条件下，增加单位压强所引起的物体体积的相对变化。强调“相对变化”同样是想让你明白为什么要除以体积V，但这里的负号挺吊诡的，需要特别说明，在温度不变时，物体的体积通常随压强的增加而减少，至于为什么，这是平衡稳定条件的推论，下文有关于平衡稳定条件的讨论。

理想气体的物态方程： p V=nRT

这个方程本来是经验定律，从实验得到。后来，丹尼尔·伯努利曾尝试通过假设气体是由大量微小粒子组成的来对波意尔定律（p∝1/V)进行解释，后来我们称之为气体动理论。具体的精彩讨论见《热物理概念——热力学与统计物理学》第2版 Blundel 著 鞠国兴 译 第6章 压强

实际气体的物态方程： \left( p+\frac{an^{2}}{V^{2}}\right)(V-nb)=nRT 。也叫范德瓦尔斯方程，或译作范德华方程，其中 a、b 是常量，其值视不同的气体而异，可以由实验测定。

什么是准静态过程？

如果我们能足够缓慢地进行某种膨胀或压缩操作，以至于气体在整个过程中始终保持平衡态，并且平滑地从一个平衡态过渡到下一个平衡态，每一个平衡态和上一个平衡态的不同仅是系统的参量有无穷小的变化。这样一个过程称为 准静态过程 （quasistatic process），因为这一过程几乎处在完全不变的静平衡。我们将会看到，在这一过程中热量虽然能被吸收或者放出，但仍然保持可逆性。与此相反，对不可逆过程，会使得系统有一个非零的变化（而不是一系列无穷小的变化），因此系统在整个过程中并不处于平衡。 ^[2]

另一个直观定义： 一个进行得无限缓慢，以致系统连续不断地经历着一系列平衡态（可在 PV图 画出）的过程。一段时间内的宏观性质改变量 \Delta p 满足 \Delta p\ll p ，且变化足够缓慢。

更严格的定义 需要引入一个 驰豫时间 的概念，详见下图第一段，摘自林宗涵的热统书

热力学中的可逆过程与不可逆过程

关于可逆过程的几种等价理解

可逆性 这个关键概念，对于后面讨论 熵 是非常重要的。学过一点点热力学的读者都知道， 热力学第二定律 描写的是由熵增表征的 不可逆过程 。因此必须先思考透彻，什么是可逆过程和不可逆过程，才有可能搞清楚热力学第二定律。这里给出以下几种等价的理解：

1. 可逆过程可以 画在pV图上 ，不可逆过程不可以。
2. 可逆过程的每一步可在相反的方向进行 而不引起外界的其他任何影响 ，反之即为不可逆过程。
3. 可逆过程是 无摩擦 的 准静态过程 ^[3] 。
4. 具有 时间反演不变性 ，若 t\rightarrow (-t) ，逆过程跟原先的过程完全一样，即为可逆过程。

可逆过程是一个既理想化又很实际的过程，说它 理想 ，指的是：没有任何摩擦的准静态过程才能算是可逆过程 ^[4] ；说它 实际 （practice），是因为：如果一个物理过程耗费的时间比系统的驰豫时间 ^[5] 小，就可以近似认为它是可逆过程。由于 严格的 可逆过程需要花费无限长的时间，因此大部分我们能称之为“可逆过程”的都只是对“实际情况”的 近似 。

熵增与不可逆过程

克劳修斯引入了熵这个概念之后，我们可以将系统与外界放一起作为一个 孤立体系 来考察，如果一个过程结束后 熵增加 了，意味着系统到达了一个更加稳定的状态，根据 热力学第二定律 （也叫 熵增加原理 ），那么这个过程就是 不可逆的 。

有了 熵 这一概念，可逆过程就可以定义为： 可逆过程是准静态过程的一个特殊情况，其中熵变是无穷小量或者不变量，而不可逆过程将导致系统熵增。

一些细节和推导见下面《热物理概念》 ^[6] 的摘录

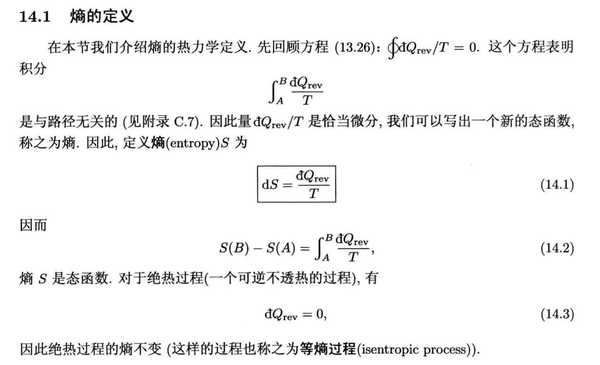
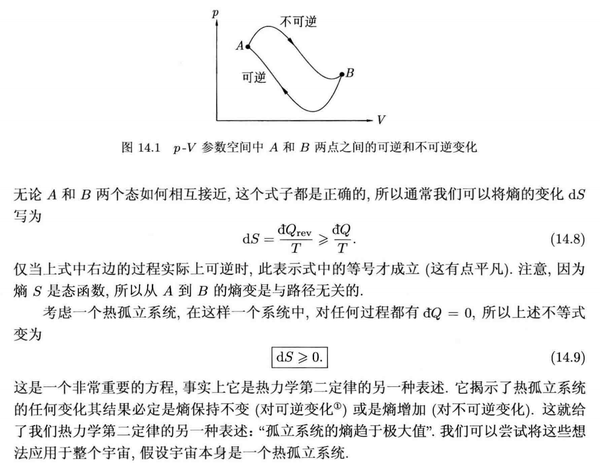
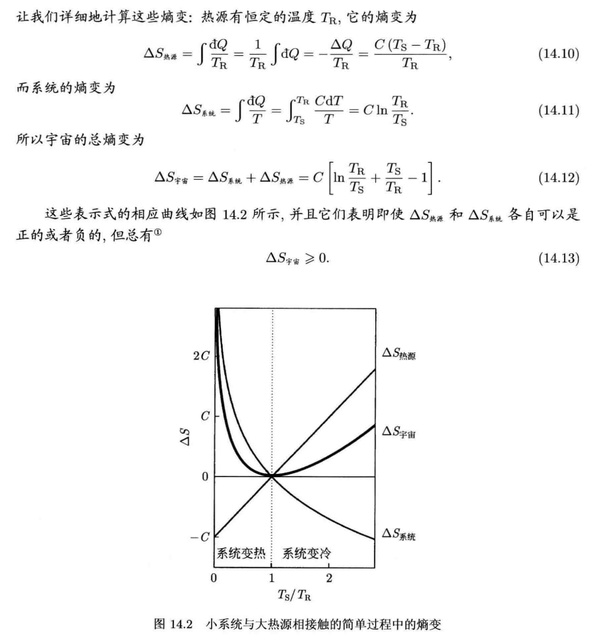
推荐阅读

可逆过程与不可逆过程极为精彩的讨论：

• 林宗涵. 热力学与统计物理学. 2版. 北京: 北京大学出版社, 2010: 25-27.
• 见Blundel, S.J, Blundel, K.M.著. 热物理概念(第2版)热力学与统计物理学. 鞠国兴, 译. 北京: 清华大学出版社, 2015: 126.
• 图省事的话可以看 @Triborg 李永乐老师的这篇 热力学“可逆过程”小辨析 。
• 可逆过程——维基百科

小游戏（证明两条pV图上绝热线不能相交）

证明： 根据热力学第二定律证明两条绝热线不能相交。

我是利用“熵是态函数”和热力学第二定律的数学表述来证明的。当然还可能有其他方法可以证明。

首先，证明 绝热线就是等熵线 。

能画在pV图上说明是可逆过程，但可逆过程不一定是等熵过程（比如卡诺循环），但 绝热 情况下的 可逆 过程肯定是 等熵 过程，于是证明了绝热线就是等熵线。

下图的说明： 第二行字，当时写得不够本质（不好），应该改成“画在pV图上的绝热线，其对应的过程是 绝热 情况下的 可逆 过程，因此绝热线就是等熵线”。第三、四行从熵的定义出发同样可以证明绝热线就是等熵线。

But Wait，两者有没有共同点呢！？

无论是可逆过程，还是不可逆过程，它们都满足 能量守恒定律 ，即热力学第一定律 ^[7] \mathrm{d}U=T\mathrm{d}S-p\mathrm{d}V ，理由见下图：

热力学第一定律（内能是态函数）

热力学第一定律讲的就是能量守恒，一句话概括：内能是态函数。

下面这个公式图片是我用LaTeX敲的，想学习怎么敲可以参考 ctex中dQ中间d加一横（đ）怎么打出来？ - 爱物理的无双麓叶的回答 - 知乎 更多实用技巧可以去 麓叶的网站 首页LaTeX专区下载《来自麓叶的LaTeX实用小技巧》

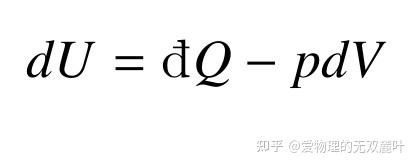
由于知乎公式编辑器似乎敲不出来不完全微分符号，下文我将不再区分这一符号，统一用 dU=dQ-pdV\tag{3}

细心的读者肯定注意到了 pdV 前面有个负号，下面几张图摘自曹则贤先生的 《物理学咬文嚼字》卷二 ，请读者慢用。

再摘录一下Mehran Kardar的Statistical Physics of Particles中的一点内容（可下载原图查看）

领略了一些好书好文之后，我们再举个例子直观地感受感受热一的本质—— 内能是态函数 。下面是焦耳（Joule）的两个著名的实验，使得绝热系统温度升高的方式有很多，可以是搅拌做功：

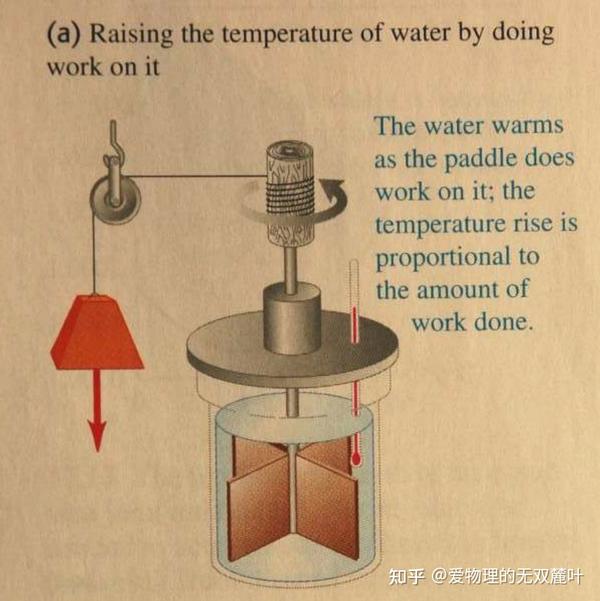
把水和叶片看作系统，其温度的升高（状态的改变）完全是重物下降做功的结果。

可以是电源做功：

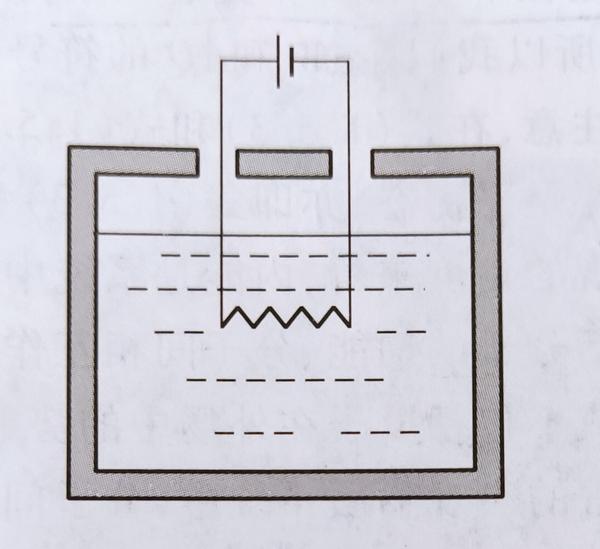
把水和电阻器看作系统，其温度的升高（状态的改变）完全是电源做功的结果。

还可以是加热：

把水看作系统，其温度的升高（状态的改变）完全是热量传递的结果。（热量这一概念将在下一节讨论）或者说，把水和酒精灯看作系统，其温度的升高（状态的改变）完全是酒精燃烧做功的结果。

如果在整个过程中把你的眼睛蒙住，只让你看初态和末态，那么你是无法看出我刚刚到底是加热了还是做功了。热量和功都是能量的形式，能量总是守恒的，这些思想构成了热力学第一定律的基础。

历史上，人们曾幻想一个不需要外界提供热量而可以不断地对外做功，后来被称为第一类永动机。热力学第一定律还有另外一种表述： 第一类永动机是不可能造成的 。

热量

许多教材并没有单独细讲热量是什么，在此摘录《热物理概念——热力学与统计物理学》中关于热量的精彩讨论。

热容

热容 C=\frac{dQ}{d\vartheta} （本文常用 \vartheta 表示温度），一句话：想让体系温度提高一度，需要给体系提供多少热量。

在此摘录《热物理概念——热力学与统计物理学》对热容的精彩讲解！

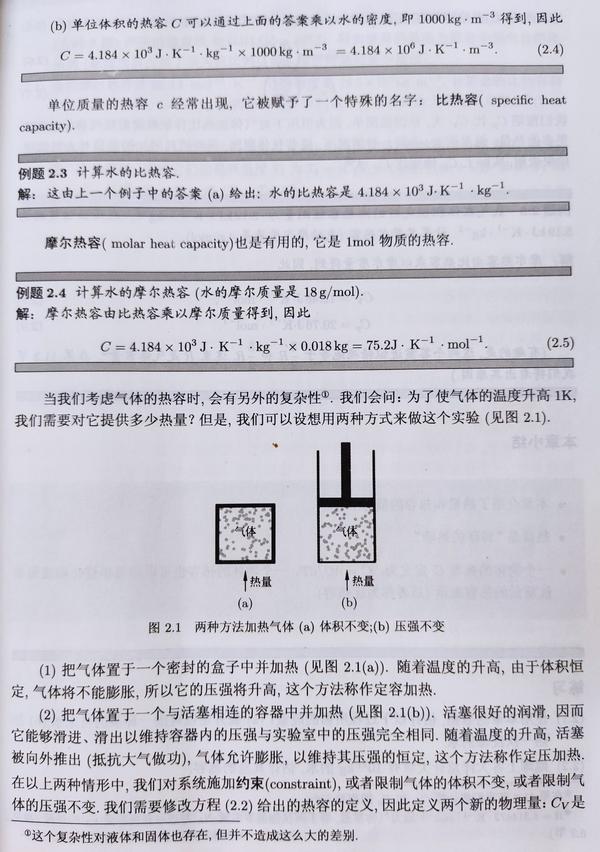
热力学发展之初经常拿气体来研究，气体体系只有两个独立变量（可以是 p、V、T 中的任意两个）。随着热力学的发展，一些定义和方程就需要修正以更具有一般性和实验的可行性，于是热容有了新定义（等容情形）： C_{v}\equiv \left(\frac{dQ}{d\vartheta}\right)_{v} ，根据热力学第一定律， dU=dQ-pdV ，等容的话，变成 dU=dQ ，于是 C_{v}= \left(\frac{\partial U}{\partial \vartheta}\right)_{v} 。自然也有另一种新定义（等压情形）： C_{p}\equiv \left(\frac{dQ}{d\vartheta}\right)_{p} ，同理根据热力学第一定律， dU=dQ-pdV ，等压的话，变成 dQ=d（U+pV）\equiv dH ，其中 H=U+pV ，于是 C_{p}= \left(\frac{\partial H}{\partial \vartheta}\right)_{p} . 其实这里的 H 就是焓（Enthalpy），符号H是Heat的首字母，翻译成焓可能是因为声母是H吧。

利用 \begin{cases} dU=TdS-pdV\\ pV=Nk_{B}T \end{cases} 可以推得 C_{p}=C_{v}+Nk_{B}

于是我们从另一个角度推得Cp比Cv大

更多内容：

经验温度与绝对温度

请原谅前文的符号混用，在此稍作解释，花体 \vartheta 和字母T都表示温度，前者是经验温度，因为我们还没严格定义温标，所以先用花体 \vartheta 表示温度。后者是在定义绝对温标之后的温度，也叫绝对温度，与经验温度是一样的。经验温度和绝对温度，不过是同一个事物在不同历史阶段下不同的称呼罢了。

在此摘录林宗涵的热统里关于热力学温标的精彩讨论以飨读者

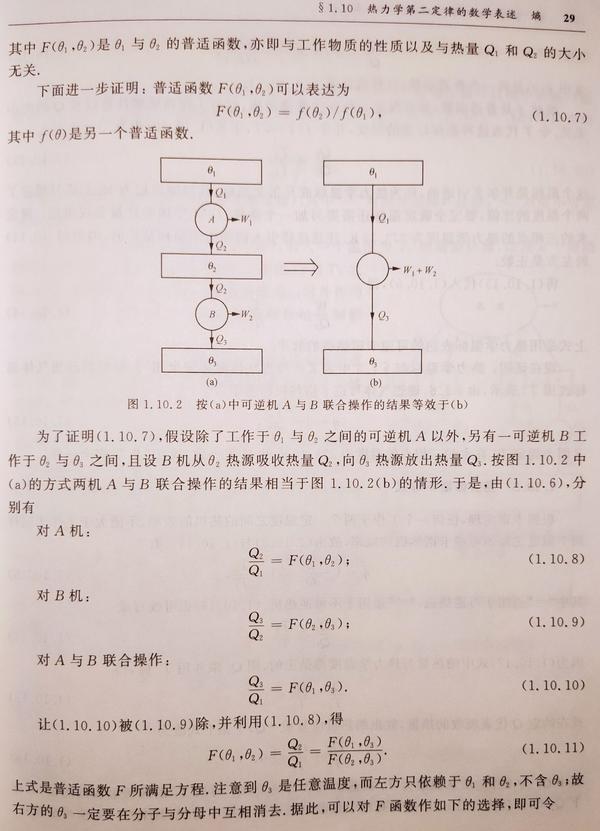
卡诺定理

早在热力学第一定律和第二定律建立之前，在 1824 年卡诺发表了他的定理：

卡诺定理：所有工作于两个一定的温度之间的热机，以可逆机的效率为最大。

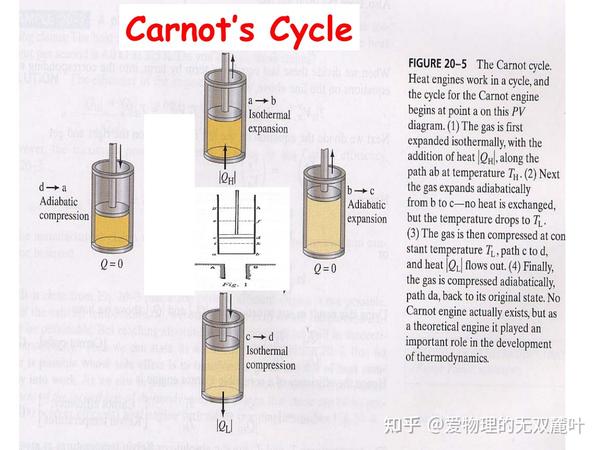
理想气体的卡诺循环

如图所示就是一个循环工作的热机，不能循环工作的热机是没有意义的、我们不感兴趣的。

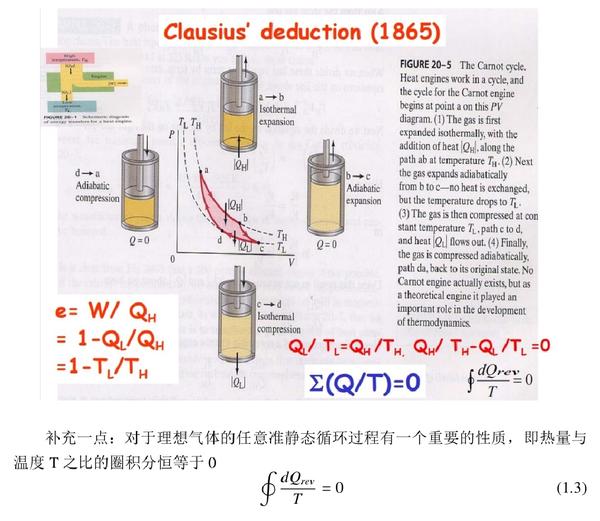
对于理想气体的任意准静态循环过程有一个重要的性质，即热量与温度T之比的圈积分恒等于0。

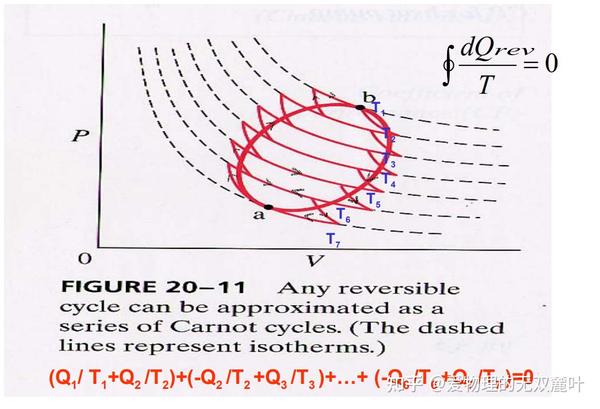
上图中，绝热线和等温线打的交叉，斜率较大的是绝热线。你自然想问为什么一次卡诺循环要经过两次绝热过程和两次等温过程，而且还是交叉着经历？那你试试看，如果从一个点经历两次等温过程和一次绝热过程，它能回到原来的起点吗？或者两次绝热过程和一次等温过程。显然都不行，经过两次绝热过程和两次等温过程的循环就是最简单的循环，再简单就构不成循环了。任意的可逆循环都可以近似当作一系列的卡诺循环。

卡诺根据两个互相矛盾的原理来证明他的定理，一个是热质说，另一个是不能有永动机。他是第一个人指出，热机必须工作于两个温度之间，把热量从高温传到低温而作功，犹如水力机作功是由于水从高处流到低处的结果一样。遗憾的是，卡诺当年用类似于热力学第一定律的方法给出的证明是错误的， 卡诺定理必须用热力学第二定律证明 。

由卡诺定理还可以得到绝对热力学温标以及熵函数。这只需要卡诺定理的一个特殊情形，即关于可逆热机的效率的定理。这是卡诺定理的一个 推论 ，可表达如下:

所有工作于两个一定的温度之间的可逆热机，其效率相等。

热力学第二定律（熵是态函数）

热量从较高温的物体流向较低温的物体，这是热力学第二定律的基础。

热二最本质的就是在告诉你，哪些过程是不可逆的，哪些过程时间反演不变性被破坏了，哪些过程初态和末态是不相当的，换句话说，存在一个态函数（后来我们知道是熵），系统在不同状态下，相应的态函数有不同的数值。

几种著名的表述：

Clausius：不可能把热量从低温热源传向高温热源，而 不引起其他变化 。

Kelvin：不可能从单一热源吸收热量完全转化为有用的功，而 不引起其他变化 。

在假想实验（thought experiment或hypothesis experiment）基础上，用反证法可以简单证明两种表述等价，即证明：如果Clausius的说法不对，那么Kelvin的说法也不对。（一般教材上都有）

不同角度看热力学几大定律（诗一样）

全微分角度 看热力学定律

热一，热量和功都不是全微分，加起来却成了全微分。

热二，热量不是全微分，热量除以温度，就是熵的全微分。

态函数角度 看热力学定律

热零，温度是态函数

热一，内能是态函数

热二，熵是态函数

一些题外话

克劳修斯表述和开尔文表述只是给我们一些概念，给一个大致的picture，真正深刻的是熵增加原理。克劳修斯表述就一句话，他研究明白了就又去研究其他的了，重构的事情留给后来人，后来人就想着怎么把热力学严密化，这也是为什么很多热统书抽象难懂的原因。实际上，真正physics的东西不一定是逻辑严密的推导，也可以是一针见血的一句话！比如卡诺定理最早提出就是类比水从高到低流的过程才能做功，热量在从高温传向低温的过程才能对外做功，单独的一个热源不能对外做功。这就很物理！

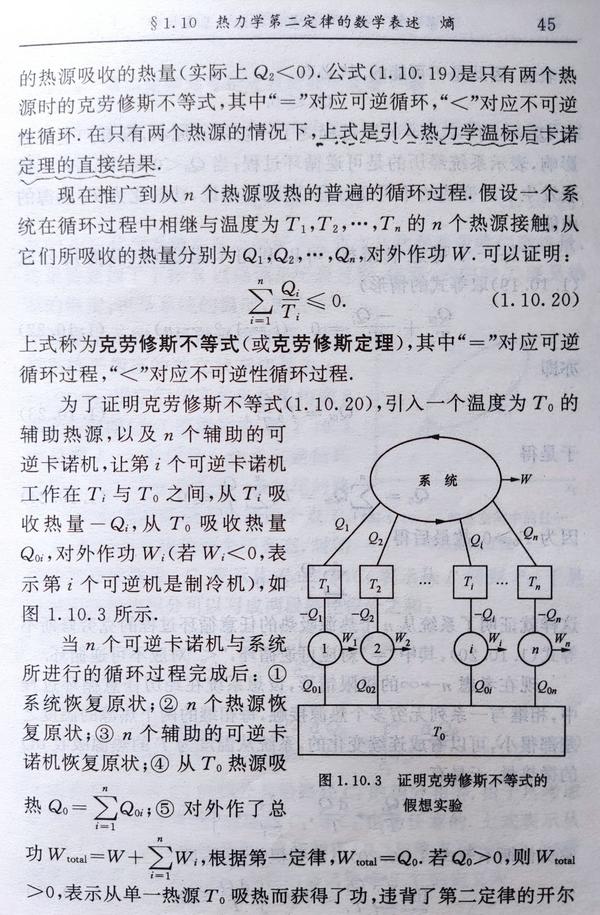
克劳修斯不等式（定理）

这部分的推导有点绕，摘录林宗涵的《热力学与统计物理学》，讲得很清楚，我是看懂了，看不懂的读者多看几遍，肯定能懂。

一些热力学量与函数的总结

1. 在热力学极限的条件下，存在广延量（如体积V，内能U、焓H、吉布斯函数G、亥姆霍兹自由能F等等），以及强度量（如压强P）
2. 响应函数（如热容C，为了使一个物体升高一定的温度，需要多少热量去加热物体）
3. 热力学势函数（如内能U、焓H、吉布斯函数G、亥姆霍兹自由能F等等），均是态函数

态函数包括熵S、焓H、吉布斯函数G、亥姆霍兹自由能F、温度T、体积V、压强p、粒子摩尔数N等等。

dQ、dW 等等都是过程量，热量、做功都跟过程有关，都要在 d 上加一删除线以示区分，表示不完全微分，如下图所示

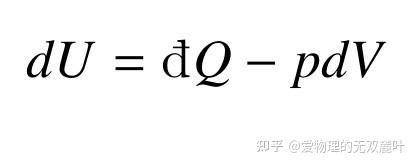
dV、dF、dT 等等都是状态量，可以写成独立变量 p、V 的函数，因此它们可以表示全微分。

定律与定理的区别

简单来说，定律是实验发现的规律，定理往往是基于某些假设得出的一般性结论。

八卦图巧记麦克斯韦关系式与热力学基本方程

首先得快速写出麦氏关系和基本方程，才能顺利得进行后续推导，所以我们需要一副强大的八卦图。

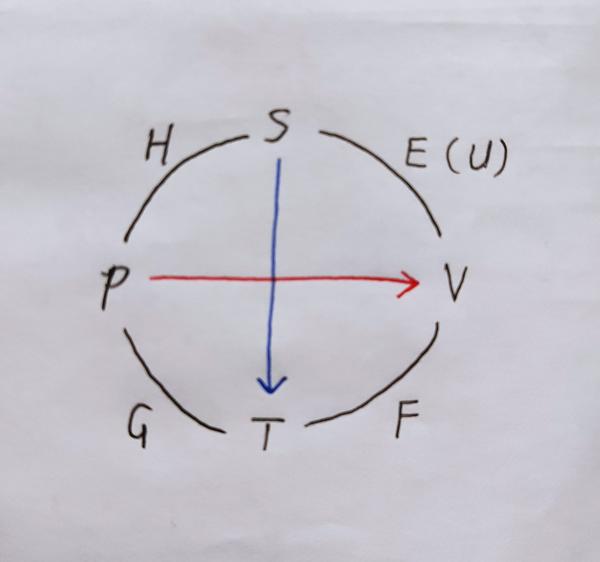
这个图可以追溯到Max Born，但又和最初玻恩提出的不太一样，记忆口诀是: The S un is pouring down his rays upon the T rees, and the brook is flowing from the P eak to the V alley. （评论区冒出了各种口诀，有比这个更好记的，比如 G ood p hysicist h as s tudied u nder v ery f ine t eacher 真的是一个词都不多余）

位于圆弧边上的四个热力学势是它们附近的两个独立变量的函数。例如内能U是体积V、熵S的（特性）函数；亥姆霍兹自由能F是V、温度T的（特性）函数；吉布斯自由能G是T、压强p的（特性）函数；自由焓H是S、p的（特性）函数。“自由”的含义在文末给出。所有热力学势还是摩尔数N的函数，这在图中并未显示。有必要补充一下， 特性函数 是什么？这是一个非常有用的概念。马休（Massieu）在1869年证明，如果适当选择独立变量，只要知道一个热力学函数，就可以通过求偏导数而求得均匀系统的全部热力学函数，从而把均匀系统的平衡性质完全确定。

各热力学势的 微分表达式 中每一项的 正负号由对角线箭头辅助记忆 。如果箭头背离自变量，则该项是正的：而箭头指向自变量则表明该项为负。结合如下等式观察图像不难掌握这一方法

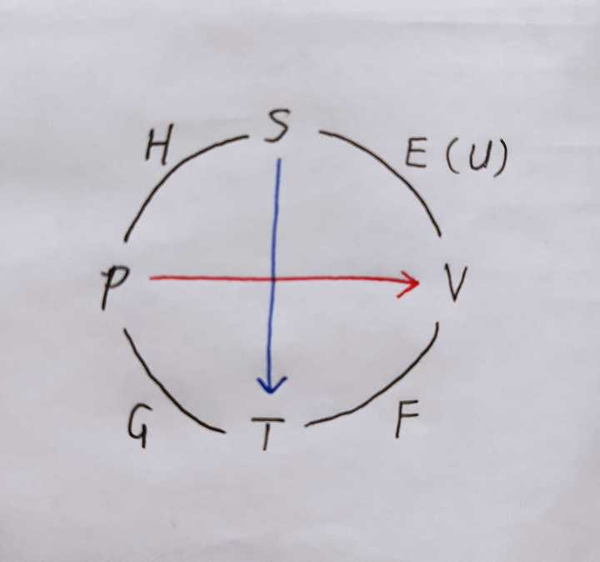
热力学势之间也可以互相表示 ，把图中的红色蓝色当作河流，水从高处向低处流，能量会降低。举例来说，从G出发到U，需要沿着pV顺流而下(能量降低，要减去pV)，沿着TS逆流而上（能量增加，要加上TS），于是得到 U=G-pV+TS

麦克斯韦关系 也非常好记忆，以 \left( \frac{\partial T}{\partial V} \right)_{S}=-\left( \frac{\partial p}{\partial S} \right)_{V} 为例，我们把注意力放在外面的大圆弧上，对照着八卦图听我讲， \left( \frac{\partial T}{\partial V} \right)_{S} 相当于 T\rightarrow V\rightarrow S ，终点是 S ，但出于惯性，再往前走一位，到达 p ，开始反过来走， p\rightarrow S\rightarrow V ，终点是 V ，得到 \left( \frac{\partial p}{\partial S} \right)_{V} ，回顾一下这两段路的终点， S 在箭头的 头部 ， V 在箭头的 尾部 ，所以符号 相反 ，即 \left( \frac{\partial T}{\partial V} \right)_{S}=-\left( \frac{\partial p}{\partial S} \right)_{V} 。读者可以自行验证一下 \left( \frac{\partial T}{\partial p} \right)_{S}=\left( \frac{\partial V}{\partial S} \right)_{p} , S 在箭头的 头部 ， p 也在箭头的 头部 ，所以符号相同，直接取等号就行了。

四个热力学势的微分表达式及其相互之间的表示，还有四个麦克斯韦关系，尽收一图，这本身就是一件很神奇的事情！夫热力学，奇术也！

外微分也能很好地推出以上关系式，请看李永乐老师的回答：

热力学中的“自由”

以上内容已作为一篇回答发表

由于本人时间精力有限，下面的更新随缘了

热力学的特性函数

特性函数的精华全凝练在刘川老师讲义的这段文字里了

化学势的引入

对于纯物质来说， 化学势 是 一摩尔 该物质的 吉布斯函数 。如果读者想用泰勒展开推导出化学势，请阅读这篇回答：

推荐阅读：《热物理概念——热力学与统计物理学》第2版 Page 251-269

相变平衡条件与稳定条件（由热动平衡判据导出）

刘川老师是变分法大佬，之前领略过他写的《理论力学》，涉及变分的单元系平衡条件就应该看他的热统讲义

下面的推导要用到拉格朗日乘子法，不记得了的读者，先把我下面这篇文章看了， 数理方法补充：

开放单元均匀系的热力学基本方程 还可以改写成式（4）这样的形式：

dS=\frac{1}{T}dU+\frac{p}{T}dV-\frac{\mu}{T}dn\tag{4}

那么 \frac{1}{T} 可以看作拉格朗日乘子 \lambda_{1} ，类似的 \lambda_{2}=\frac{p}{T} ， \lambda_{3}=-\frac{\mu}{T} 。有了这些解说，读者再接着看会轻松一些。

关于相变平衡条件，更详尽的讨论可参阅林宗涵的《热力学与统计物理学》page80~90，相变平衡的稳定条件我觉得非常精彩，摘录在下面以飨读者

热力学中的勒让德变换&Gibbs Sum

看这个视频： P17Ⅰ 第17讲 Gibbs Sum

亥姆霍兹自由能的引入

看这个视频： P9Ⅰ 第9讲 Helmholtz Free Energy

热力学中的雅可比行列式

玻尔兹曼系统、玻色系统和费米系统

这是我写的回答，整理到这里

统计物理导出热力学量表达式（文末有考点透露）

对比玻尔兹曼统计导出的热力学量表达式与正则系综导出的热力学量表达式，只相差一个N（系统总粒子数），这个可以从配分函数上理解，玻尔兹曼系统的配分函数里面的能量是单粒子的能量，而正则系综的配分函数是系统总能量。

正则系综和巨正则系综的适用范围是，宏观参数不变的系统，即系统处在平衡态。更细致地说，正则系综适用于与外界有能量交换的平衡系统，巨正则系综适用于与外界既有能量交换又有物质交换的平衡系统。正则系综到巨正则系综，从闭系到开系。

正则系综应用非常广泛，同学们要重点掌握。期末考试最后一道大题就是考正则系综。（2021.7.2）

黑体辐射

曹则贤老师对黑体辐射已经有精彩详尽的讨论， 黑体辐射公式的多种推导及其在近代物理构建中的意义(I) 和 （II）

这里我只针对一些关键概念给出启发性较强的理解。

1. 波动，就是“振动的传播”。“波动”的概念建立在“振动”之上，“波动”的概念是“振动”与“传播”这两个概念的结合。
2. 一维波动的数学描述，是一个关于x和t的二元函数（即多元函数）。而振动只需要一元函数即可描述。

时间和空间周期性是波动的重要特征！

波矢k 的大小表征单位距离内的相位变化量。（”波矢“的概念非常重要，在后续的电磁学、电动力学、固体物理、量子力学中经常出现）

圆频率ω 表征单位时间内的相位变化量。

时间和距离的变化都会导致相位的变化，从而导致振动情况的不同！

以上概念能够帮助大家理解教材中玻色统计部分关于光子气体的推导。

热统好文分享

热统好书推荐

《热物理概念——热力学与统计物理学》Blundel 著 鞠国兴 译

这本书很适合入门，属于把热力学和统计力学混在一起讲的书，热力学部分对很多基本概念的讨论有一定深度，有非平衡态统计力学的拓展讨论。

但是热力学部分比较简洁，需要搭配汪志诚、王竹溪或者林宗涵的书进一步学习，否则无法满足国内很多高校的考纲要求。我自己的标配是鞠国兴译的《热物理概念——热力学与统计物理学》加汪志诚的热统，汪志诚的书看不懂时，就去翻林宗涵的热统。

热统网课分享

需要的基础：微积分、原子物理学（特别是原子的精细结构，是理解第1和第2讲的基础）

配套教材：Charles Kittel和Herbert Kroemer的 Thermal Physics

这个视频前几讲比较难，从下面这几张图片，是我做的听课笔记，就可以看出难度。我也是听第二遍才完全明白的，前几讲坚持住，后面就好懂多了。关键就在前面几讲，是理解热统的基础。

不知不觉，这里成了我安放听课笔记的地方。

非广延统计力学

作者注

本文只是一个微不足道的尝试，不具备一般教材的完整性和可读性。只是希望我的一些经验能多多少少帮到读者，以感谢读者们对我的支持！

本文摘录的图片不代表本人观点。由于作者学识和能力有限，文中难免会有错误之处，可在评论区指正！为方便读者点击跳转，下面的参考文献格式不完全正确，请读者谅解！

参考文献

1. Introductory Statistical Mechanics, Second Edition by Roger Bowley, Mariana Sánchez
2. Thermodynamics and an Introduction to Thermostatistics by Herbert B. Callen
3. 《热物理概念——热力学与统计物理学》第2版 Blundell 著 鞠国兴 译 清华大学出版社
4. Statistical Physics of Particles by Mehran Kardar 这本书在b站有配套视频 MIT Mehran Kardar 统计物理学 Statistical Mechanics [中英双字幕]_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
5. 复旦大学 金晓峰教授的热力学与统计物理课程 http://www. icourses.cn/sCourse/cou rse_5922.html bilibili也有搬运 热力学与统计物理（复旦大学）_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
6. 统计物理学 复旦大学 苏汝铿主讲 bilibili有搬运 【物理】统计物理学 复旦大学 苏汝铿主讲_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
7. 《物理学咬文嚼字》卷二 by 曹则贤
8. 《热力学》by 王竹溪（第二版）
9. 热力学与统计物理讲义 by 刘川 北京大学物理学院
   
   

参考

1. ^ 可以私信我要电子书。
2. ^ [英]Blundel, S.J, [英]Blundel, K.M.著. 热物理概念(第2版)热力学与统计物理学.鞠国兴, 译. 北京: 清华大学出版社, 2015: 126.
3. ^ 如果我们能足够缓慢地进行某种膨胀或压缩操作，以至于气体在整个过程中始终保持平衡态，并且平滑地从一个平衡态过渡到下一个平衡态，每一个平衡态和上一个平衡态的不同仅是系统的参量有无穷小的变化。这样一个过程称为准静态过程（quasistatic process），因为这一过程几乎处在完全不变的静平衡。我们将会看到，在这一过程中热量虽然能被吸收或者放出，但仍然保持可逆性。与此相反，对不可逆过程，会使得系统有一个非零的变化（而不是一系列无穷小的变化），因此系统在整个过程中并不处于平衡。
4. ^ 但可逆过程是允许吸放热的，见[英]Blundel, S.J, [英]Blundel, K.M.著. 热物理概念(第2版)热力学与统计物理学. 鞠国兴, 译. 北京: 清华大学出版社, 2015: 126.
5. ^ 原本处于平衡态的系统经过扰动后重新恢复到平衡态的用时。
6. ^ [英]Blundel, S.J, [英]Blundel, K.M.著. 热物理概念(第2版)热力学与统计物理学. 鞠国兴, 译. 北京: 清华大学出版社, 2015.
7. ^ 也叫“热力学基本方程”，我更喜欢这个叫法。