信道编码系列(三):伽罗华域(Galois Fields)
有限域,也称为伽罗华域(Galois Fields,简写为GF,该命名是为纪念法国数学家 Evariste Galois)。它是纠错码(尤其是BCH码和RS码的基础)理论的重要基础。在本文中,我们通过两方面来介绍有限域。首先介绍素数域这一新的代数系统(algebraic system);接着介绍基于素数域的扩展域—伽罗华域的构造方法及对重要的一些定理,这些对纠错码理论有重要的意义。
1、素数域(prime field)
1.1、域的引入及具体的实例
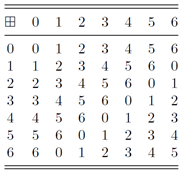
域是一种定义了域中元素两种数学运算的代数系统,域由全体元素的加法集合以及非零元素的乘法集合构成。具有有限个元素的域,称为有限域。考虑这样一组整组构成的域 G = {0, 1,2,3,….. p -1}。其中p为素数,定义两种数学运算分别为 modulo-p加法和 module-p乘法。当p=7时,modulo-7的加法集合如下表所示,满足几个性质:(1)封闭性:集合中任意两个元素相素相加后的结果,仍然属于该集合(2)满足加法交换律 a+b = b+a,从表中也可以看出,相加后的矩阵是以主对角线为对称轴的对称矩阵。(3)满足加法结合律 (a+b)+c = a+(b+c)。注意,这里的+运算符是module-7的加法。
域中非零元素的modulo-7的乘法集合如下表所示,该集合满足:(1)封闭性:集合中任意两个元素相素相乘后的结果,仍然属于该集合(2)满足乘法交换律 a*b = b*a,从表中也可以看出,相乘后的矩阵是以主对角线为对称轴的对称矩阵。(3)满足乘法结合律 (a*b)*c = a*(b*c)。注意,这里的*运算符是module-7的乘法。
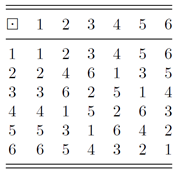
备注:一定要选择 p 为素数,这样才能使得modulo-p乘法具有封闭性。假设 p =6,那么元素3和元素4,进行modulo-6乘法后,得到结果是 0,零元素不在乘法集合中。
根据GF( p )上面的定义,可以得到如下的定理:
定理1: 如果α 是有限域GF( q )中的非零元素,那么有 α^{q-1} =1 。
利用模乘规则和乘法集合的封闭性,容易证明出该定理,具体过程如下:

1.2、基于域中元素的多项式
在基础数学中,多项式可以表示为如下形式,其中 f_i 为多项式的系数,系数可以是任意整数、甚至复数,多项式可以进行加法、减法、乘法、除法等操作。
f(X)= f_0+f_1 X+f_2 X^2+f_3 X^3+⋯f_n X^n
如果我们将多项式的系数限定于有限域GF( q )中的元素,并且基于有限域中的运算规则重新定义多项式的加减乘除操作,那么这样的多项式集合称为 基于有限域的多项式。假设有两个基于有限域的多项式a(X)和b(X):

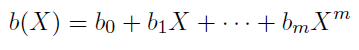
定义多项式的加法 :

其中 + 是指在GF( q )中的 modulo- q 加法。
定义多项式的乘法 :

其中:
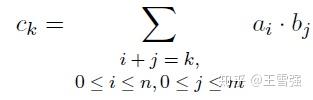
多项式的减法定义为:

其中 a_i-b_i =a_i+(-b_i) , -b_i 称为 b_i 元素的加法逆,与 b_i 满足 (-b_i)+b_i=0 ,上述 + 是在GF( q )中的 modulo- q 加法。
定义多项式的除法 :
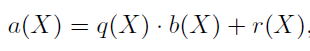
其中q(X)和r(X)分别称为商和余数,显然deg(r(X)) < deg(b(X))(deg称为多项式的阶数,即多项式的最高阶数),该操作也称为欧几里德除法算法,下面通过基于GF(5)中的实例来说明基于有限域的多项式除法。

定义1: 如果m阶多项式 p(X)=p_0+p_1X+p_2X^2+...+p_{m-1}X^{m-1}+X^{m} 不能被基于有限域GF( q )中的任何多项式整除,称 p(X) 为不可约多项式。
定理2: 有限域GF( q )任意的m阶不可约多项式 p(X) ,都可以整除 X^{q^m-1} ,即 p(X) 为除数, X^{q^m-1} 为被除数,相除后余数为0。
定义2 :如果不可约多项式 p(X)=p_0+p_1X+p_2X^2+...+p_{m-1}X^{m-1}+X^{m} 能够整除 X^n-1 的 n 的最小整值取值为 n=q^m-1 ,那么称 p(X) 为本原多项式。
在下一章中我们将看到,本原多项式对于构造伽罗华域至关重要,下面的中列出了在各种素数域中的本原多项式。


例如,对于本原多项式 p(X) =X^5+X^2+1 ,对不同的 X^n-1 的 n 的取值进行尝试,可以发现,能够被 p(X) 整除的最小的 n=31 ,具体而言:
X^{31}-1=(X^5+X^2+1)*(X^{26}+X^{23}+ X^{21}+X^{20}+ X^{17}+ X^{16}+X^{15}+ X^{14}+ X^{13}+X^9+X^8+X^6+ X^5+ X^4+X^2+1)
2、伽罗华域的构造及重要性质
2.1 扩展域(extenstion field)的构成
扩展域的构造从本原多项式开始:对于基于素数域 GF(p)=\{0,1,2,3,...p-1\} 的本原多项式 p(X)=p_0+p_1X+p_2X^2+...+p_{m-1}X^{m-1}+X^{m} 。由本原多项式的定义可知, p(X) 在素数域上是不可约的,因此 p(X) 的根不可能在素数域 GF(p) 上找到,它们存在于一个更大的域中。下面我们来寻找这个域,
假设α是 p(X) 的一个根,那么我们有:
p_0+p_1\alpha+p_2\alpha^2+...+p_{m-1}\alpha^{m-1}+\alpha^{m}=0
因为 p(X) 又可以整除 X^{q^m-1} -1 ,我们又得到
\alpha^{q^m-1} -1=0 , 即 \alpha^{q^m-1} =1
根据上式,可以构建基于α幂次方的集合:
F=\{0,1,\alpha,\alpha^2, \alpha^3, ..... \alpha^{m-2} \}
定义F中的乘法运算:

将多项式 X^i 除以 p(X) ,得到 X^i = q(X)p(X)+a_i(X) ,其中 a_i(X) 是余数,由于 p(X) 的最高阶数为m,因此余数 a_i(X) 的最高阶数为 m-1,将X替换成α,另有 p(\alpha)=0 ,上式可以得到:
\alpha^i=q(\alpha)p(\alpha)+a_i(\alpha) = a_0+a_1x+a_2x^2+...+a_{m-1}x^{m-1}
可以得到,任意一个 \alpha 的幂次方都可以表示成m-1阶或更小阶数的α多项式。根据这个重要的结论,定义 F 中的加法运算:

其中的系数 a_{i, m-1}+b_{j, m-1} 相加运算为GF( p )中的 modulo- p 加法。
可以证明, F 集合构成了一个具有 p^m 个元素的域,用符号 GF(p^m) 表示, GF(p^m) 称为 GF(p) 的扩展域, GF(p^m) 有三种表示形式,下面用一个实例来展示 GF(2^5) 中的元素构成及表示。

2.2、 伽罗华域的重要性质
在本节中,给出几个伽罗华域的重要性质,这些性质对于构造纠错码是对于有限域(也称伽罗华域,Galois field) GF(p^m) ( p 为素数)。
定理3、 如果 f(X) 是 GF(p) 上的多项式,β是 GF(p^m) 中的元素,如果β是f(X)的一个根,那么对于任意正整数t, \beta^{q^t} 也是 f(X) 的一个根。 \beta^{q^t} 称为 \beta 的共轭(conjugate)


定理4: GF(q^m) 中的 q^m 个元素形成了 X^{q^m}-X 的所有根。
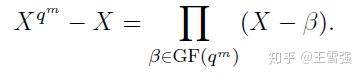
定理5: \beta 是 GF(q^m) 中的元素,以 \beta 为根的阶数最小的多项式,称为最小多项式Φ(X),即Φ(β)=0,进一步,Φ(X)具有如下形式:
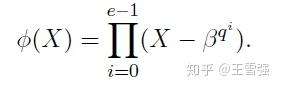
其中 e是最小的正整数,使得 \beta^{q^e} = β。
生成最小多项式一个具体实例如下:

