7 个回答
这个问题略犀利... 分数量子霍尔效应(Fractional Quantum Hall Effect ~ FQH)是霍尔效应家族里最复杂也是最 fancy 的之一... 下面是豆瓣物理组 E 大为霍尔效应家族做的一副图, FQH 就是最右下角的那个.
问这个问题的人想必没有太多凝聚态物理的背景, 我还是尽可能从头讲起.
- 霍尔效应
高中物理课上想必大家都学过霍尔效应: 将一块导体(半导体也可以)放置在一个磁场内, 然后通电流. 在垂直于磁场和电流的方向会产生电压. 这个效应最早是1878年由美国物理学家 Hall 在读 PhD 时发现的. 这个效应非常有用, 比如我们可以基于此方便而又准确地测量空间中某处磁场的大小.
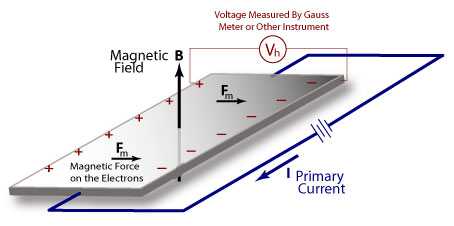
造成这个现象的原因大家是熟知的: 电子在磁场中受到 Lorentz 力而偏转, 在导体两端积累, 在导体中建立起电场从而在产生电势差. 这个电压被称为霍尔电压. 霍尔效应一个显著的特征是 霍尔电压与磁场强度成正比 . 下面是 Hall 当年发现该效应时的原始数据:
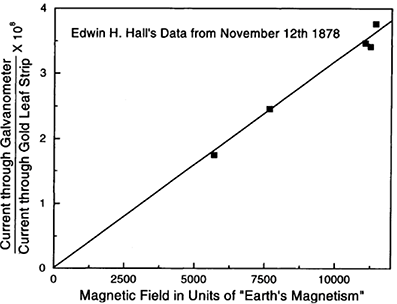
- 量子霍尔效应
霍尔效应是在三维的导体中实现的, 电子可以在导体中自由运动. 如果通过某种手段将电子限制在二维平面内, 在垂直于平面的方向施加磁场, 沿二维电子气的一个方向通电流, 则在另一个方向也可以测量到电压, 这和霍尔效应很类似.
在整整一百多年后的1980年, 德国物理学家 von Klitzing 发现了所谓的量子霍尔效应. 之所以要等这么久才能实现这一效应, 主要是由于理想的二维电子气难以实现. 在半导体技术高度发展之后, 人们才能在"金属-氧化物-半导体场效应晶体管"(MOSFET)中实现比较理想的二维电子气. 除此之外, 观察到这一效应还需要极低温(1.5K)和强磁场(18T). von Klitzing 因此获得了1985年诺贝尔物理学奖.
量子霍尔效应与霍尔效应最大的不同之处在于横向电压对磁场的响应明显不同. 横向电阻是量子化的, 由此我们称这一现象为量子霍尔效应:
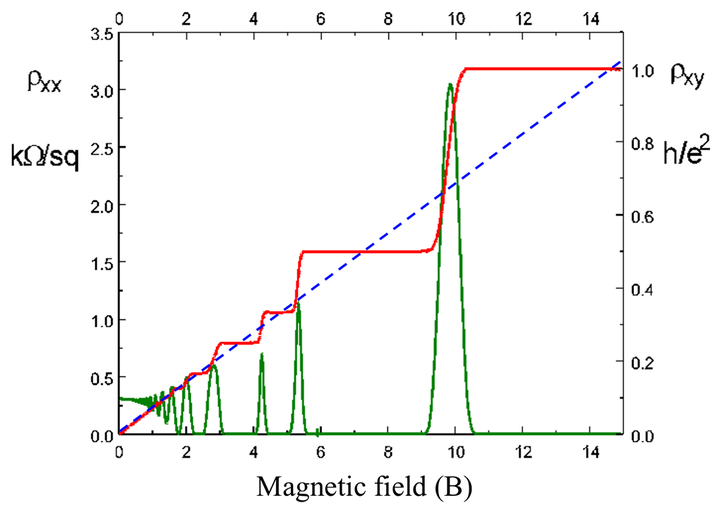
尽管从整体趋势上看, 横向电阻(图中红线. 电阻的定义为电压/电流, 实验时电流恒定, 因此横向电阻就相当于横向电压)随着磁场强度增大而线性增大, 但在这一过程中却形成了若干横向电阻不变的平台. 这些平台所对应的电阻是"量子电阻" \frac{h}{e^2} 除以一个整数 n, 对应图中平台的"1, 0.5, 0.33, 0.25, 0.2"等位置. 量子霍尔效应也称作整数量子霍尔效应(Integer Quantum Hall Effect ~ IQH). 原始霍尔效应所对应的区域是磁场强度 B 很小区域. 从图中可以看见磁场强度很小时横向电阻与磁场强度确实成线性关系.
除此之外, 量子霍尔效应中的纵向电阻(图中绿线)的随磁场的变化也很奇特: 在横向电阻达到平台时, 纵向电阻竟然为零! 在原始霍尔效应时, 纵向电阻随磁场几乎是不变化的, 这对应图中磁场强度很小时纵向电阻确实近似是一个常数.
量子霍尔效应其背后对应的物理机制, 通俗地说, 可以用下图来解释:
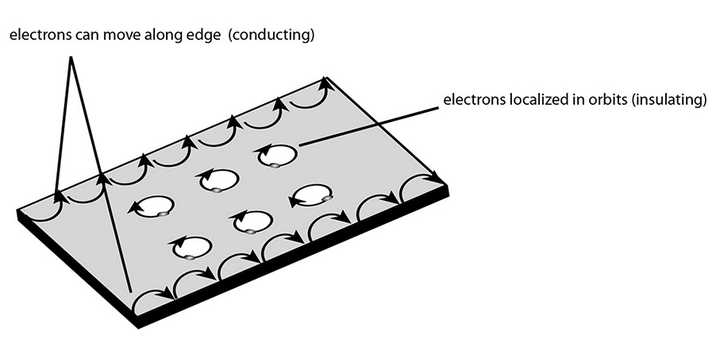
在强磁场下, 导体内部的电子受 Lorentz 力作用不断沿着等能面转圈(Lorentz 力不做功!). 如果导体中存在杂质, 尤其是带电荷的杂质, 将会影响等能面的形状. 实际上, 导体内部的电子只能在导体内部闭合的等能面上做周期运动, 而不能参与导电. (因此在 很纯净的样品中反而观察不到量子霍尔效应! )
在量子霍尔效应中, 真正参与导电的实际上是电子气边缘的电子. 而边缘的电子转圈转到一半就会打到边界, 受到反弹, 再次做半圆运动, 由此不断前进. 这种在边界运动的电子, 与通常在导体内部运动的电子不同, 它不是通过不断碰撞, 类似扩散的方式前进的. 而是几乎不与其他电子碰撞, 直接到达目的地, 像一颗子弹. 因此这种现象在物理学中被称为弹道输运(ballistic transport). 显然在这种输运机制中产生的电阻不与具体材料有关, 只与电子本身所具有的性质有关. 因此横向电阻总是 \frac{h}{ne^2} , 其中 n 是一个正整数. 之所以与 n 有关, 粗略地说, 是因为磁场小到一定的程度, 就会同时使更多的电子进行弹道输运. 进行的电子越多, 横向电阻越小.
量子霍尔效应中的这种参与导电的"边界态"是当今凝聚态物理重要的兴趣所在之一. "边界"和"表面"有其重要的拓扑性质, 所谓"拓扑绝缘体"也与它们紧密相关. 事实上, von Klitzing 是在德国的 Würzburg 大学发现的量子霍尔效应. 28年后, 同样是在 Würzburg 大学, 同样是 von Klitzing 之前所在的研究组, Molenkamp 等人第一次在实验上发现了拓扑绝缘体: 碲化汞. 由此也可以发现 一项重要的工作的完成不是一蹴而就的, 其背后必然有着深厚的积累.
- 分数量子霍尔效应
之前在量子霍尔效应中, 曾经提到想要观察到这个效应需要保证样品中存在一定数量的杂质. 如果我们考虑一个极其纯净的样品, 那会观察到什么现象? 在 von Klitzing 的实验中, 实现二维电子气的 MOSFET 中的氧化物和半导体是二氧化硅和硅. 但二氧化硅的纯度很难提升. 1982年, 华人物理学家崔琦, 德国物理学家 Stormer 等人在 Bell 实验室用 AlGaAs/GaAs 异质结代替二氧化硅和硅, 因为通过分子束外延(MBE)技术可以生长出超纯的异质结, 从而实现极其纯净的二维电子气. 他们发现, 横向电阻 \frac{h}{ne^2} 的 n 不仅可以取正整数, 还出现了 n=1/3 这样一个分数的平台! 这就是分数量子霍尔效应. 之后他们制造出了更纯的样品, 更低的温度, 更强的磁场. 85mK 和 280kG, 这是人类第一次在实验室中实现如此低的温度和如此强的磁场(地磁场是 mG 的量级). 这样的实验技术令人叹为观止.

他们也因此观察到了更加丰富的结构(下图不是原始结果而是实验技术进一步提高之后的结果. 参考:
The Fractional Quantum Hall Effect. ):
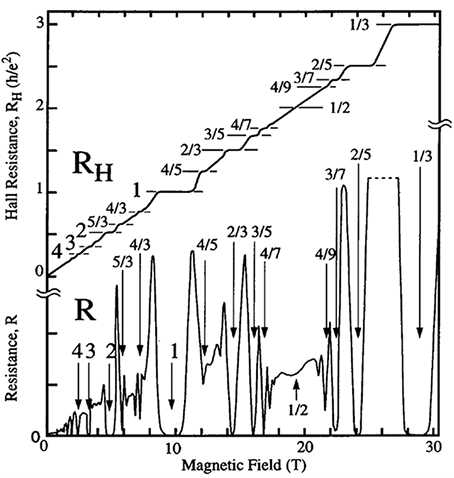
根据之前对 n 的解释, n 不可能是分数, 因为不可能有分数个电子同时进行弹道输运. 之前的解释不适用! 最早美国物理学家 Laughlin 给出了一个比较令人信服的解释, 他因此和崔琦与 Stormer 分享了1998年诺贝尔物理学奖.
导体中电子中的相互作用主要有: 电子-杂质, 电子-电子. 之前在解释整数量子霍尔效应时, 我们忽略了电子与电子的相互作用. 而在现在这种样品极为纯净的情况下, 我们不能忽略这一相互作用. 因为电子之间的相互作用很强, 导致电子之间的关联也很强. "牵一发而动全身", 这时我们再用"一个电子"的图像去看问题就不合适了. 为了解决这一问题, 其中一种看法是"混合粒子". 就像质子是由三个夸克组成的一样, 我们可以人为地将处于磁场中的(电子)看作没有磁场时的(电子+量子磁通量). 我们将(电子+量子磁通)人为地看成一个整体, 即"混合粒子". 在这种看法下, 我们会发现"混合粒子"之间近似没有相互作用. 这样我们就将一个强相互作用的问题转化成了一个无相互作用的问题. 对于 n=1/3 的情形, 就是一个电子与三个量子磁通相结合成了一个"混合粒子". 这样 所谓分数量子霍尔效应就是"混合粒子"的整数量子霍尔效应 . 由于一个电子现在附着了三个量子磁通, 这就解释了分数量子霍尔效应中的 n=1/3. 示意图如下, 穿过电子的三根线即为三个量子磁通:
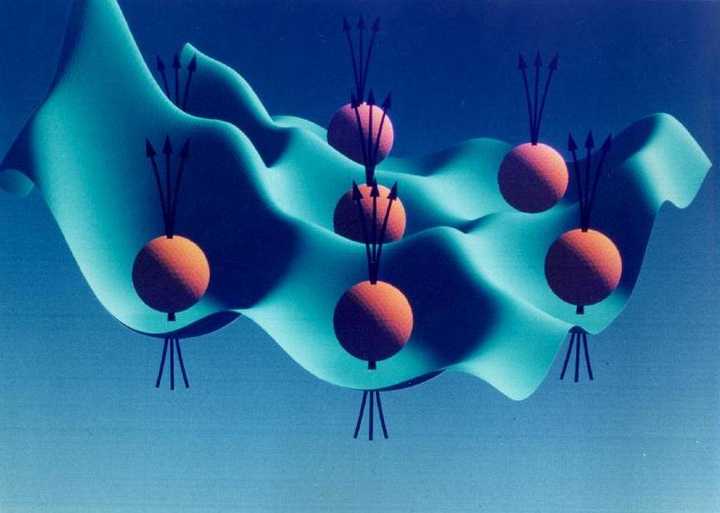
这一解释虽然看起来合理, 但至今也有很多争议. 分数化是强关联系统一个典型特征. 而强关联系统是当今凝聚态物理学重要的一个分支. 高温超导等许多重要的现象都被认为与此相关. 在这个领域还有大量问题等待人类去回答和探索.
有关量子霍尔效应有一篇十分入门的综述:
http:// arxiv.org/abs/0909.1998. 推荐给感兴趣的物理系同学.
关于整数量子霍尔效应的故事大家都很清楚了,加磁场的二维电子气会出现横向电阻的整数平台,这些平台对应了费米面下填充的朗道能级数目,所以是量子化的。
那么当磁场进一步的增大的时候,会出现什么样的现象呢?
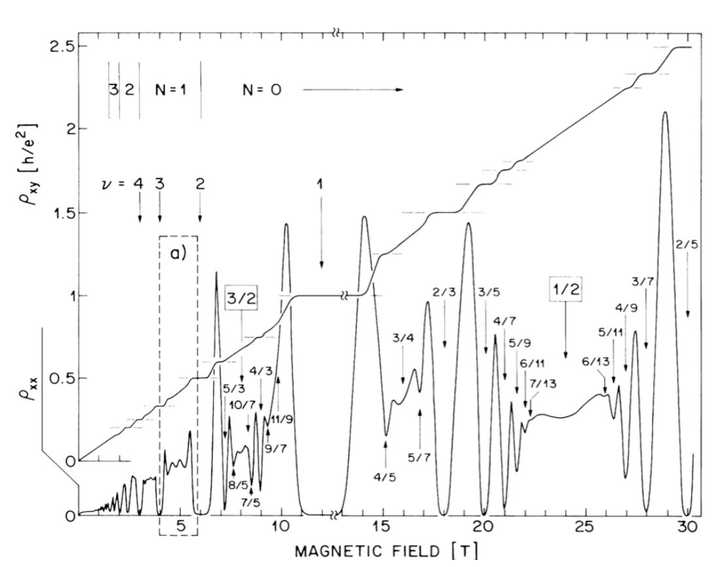
如上图所示,纵向电阻会在一些分数的地方产生平台,我们会发现这些平台的填充数基本都是分母为奇数的分数,比较显眼的是 1/3,1/5,1/7 等等分母为奇数然后分之一的分数(当然也有 1/2 )。解释这些平台的理论是花样繁多的,但是有一点是我们的共识,那就是与整数情况不同,那里我们将电子视为相互之间没有作用的自由电子,在分数量子霍尔效应中电子之间的相互作用不能被忽视。这里我们简单采用 Chern-Simons 理论稍微解释一下为啥这里填充数是类似 \frac{1}{奇数} 的形式。
一、任意子和规范场通量
在开始之前,需要对研究对象进行一点点说明。大家对玻色子和费米子都是比较熟悉的,它们的一个重要区别在于“交换”,前者波函数交换不变号,后者多一个负号。然而在二维情况下还可能存在任意子,在相互交换之后波函数会多出来一个 \exp(i \eta \pi) ,这里 \eta 对于玻色子是 2n ,对于费米子是 2n+1 。我们知道,所谓的“交换”也可以看成一个绕着另一个转半圈。假设在一个规范场里面,一个电荷为 q 的粒子绕着一个轨道绕了一圈,那么它的波函数会多一个相位,即多一个 \exp(iq\Phi) ,其中 \Phi 为规范通量。现在假设两个任意子交换了位置,然后再交换位置,那么会得到一个相位 \exp(2i \eta \pi)=\exp(iq\Phi) ,所以有
2\pi \eta =q\Phi
现在我们的任务就是看看电荷和规范场通量之间的关系就好了。
二、Chern-Simons 拉格朗日量
首先我们观察一下 Chern-Simons 项
L=-\frac{1}{2}k\varepsilon^{\mu \nu \lambda}a_\mu \partial_\nu a_\lambda
简单计算会发现它是 U(1) 规范场, a_\mu 是规范场矢势,但是其自身没有动力学的,我们需要注入一个电流来驱动
L=-\frac{1}{2}k\varepsilon^{\mu \nu \lambda}a_\mu \partial_\nu a_\lambda+a_\mu J^\mu
可以得到运动方程
J^\mu=k \varepsilon^{\mu \nu \lambda} \partial_\nu a_\lambda
这里我们明白了,CS场对其中流动的流是有一个约束的,由这个约束我们可以计算电荷和规范场通量之间的关系了:
\rho=-kb,q=-k\Phi
带回去,得到任意子相位
\eta=-\frac{q^2}{2\pi k}
现在把电磁场加入进来:
L=-\frac{1}{2}\frac{s}{2\pi}\varepsilon^{\mu \nu \lambda}a_\mu \partial_\nu a_\lambda+\frac{e}{2\pi}\varepsilon^{\mu \nu \lambda}A_\mu \partial_\nu a_\lambda+j^\mu a_\mu
第一项是 Chern-Simons 项,其给出电流,第二项是电磁场与 CS 电流之间的耦合,最后一项表示一个电流源与这个场的耦合。
\partial_\nu \frac{\partial L}{\partial(\partial_\nu a_\mu)}=\frac{1}{2}\frac{s}{2\pi}\varepsilon^{\mu \nu \lambda}\partial_\nu a_\lambda-\frac{e}{2\pi}\varepsilon^{\mu \nu \lambda}\partial_\nu A_\lambda
\frac{\partial L}{\partial a_\mu}=-\frac{1}{2}\frac{s}{2\pi}\varepsilon^{\mu \nu \lambda}\partial_\nu a_\lambda+j^\mu
得到
J^\mu_{CS}=\frac{e}{2\pi s}\varepsilon^{\mu \nu \lambda}\partial_\nu A_\lambda+\frac{1}{s}j^\mu
以上式子可以解释为:向体系里面注入一个激发 j^\mu 和电磁场 A_\lambda ,它会产生一个电流 J^\mu_{CS} 。
三、有源与无源的情况
3.1 无源——横向电导
如果我们把准粒子源关闭 j^\mu=0 ,那么我们得到一系列方程组:
J^0_{CS}=\rho=-\frac{e}{2\pi s}B
J^1_{CS}=-\frac{e}{2\pi s}E^2 , J^2_{CS}=\frac{e}{2\pi s}E^1
这就说明一个y方向的电场会产生一个x方向的电流,而电流的表达式为
I_x=(-e)J^1_{CS}=\frac{e^2}{2\pi s}E_y \to \frac{e^2}{\hbar s}E_y ,(1\to\hbar)
这里还是先保持 \hbar=1 ,只是做个样子
\sigma_{xy}=I_x/E_y=\frac{e^2}{h} \frac{1}{s}
这样我们只需要证明 s 是奇整数就行了。
3.2 有源——元激发特性
现在我们假设在 0 位置注入准粒子l,这里 l 是整数,代表 a_\mu 中 l 荷的准粒子(它同时还带有 A_\mu 中的电荷 q)。于是我们写出电流表达
-eJ^0_{CS}=\frac{e^2}{2\pi s}B-\frac{el}{s} \delta^2(x)
右边第一项是从 FQH 基态得到的电荷密度,第二项则为注入准粒子带来的额外电荷。于是我们读第二项知道l对应的电荷为 -el/s ,同时其携带了 2\pi l/s 的通量。
四、为什么 s 是奇整数
现在我们考虑两个粒子交换的情况。假设两个粒子 l_1=l_2=l ,现在相互交换位置,得到的相位为
\delta \Phi=2\pi \frac{l_1 l_2}{s}=2\pi \frac{l^2}{s}
然后我们因为只是绕了半圈,所以有
\pi \eta=\pi \frac{l^2}{s} \Rightarrow \eta=\frac{l^2}{s}
所以,我们得到一个结论:FQH 激发态中的准粒子在 a_\mu 场里面携带荷 l ,同时对应携带 A 场里面的电荷 -el/s ,同时交换两个准粒子带来相位变化 l^2/s
我们现在考虑元激发是一个真正的电子,那么会是什么样的情况呢?首先,真正的电子携带电荷 -e ,其对应了 a 场核 l=s ,交换两个电子的相位变化是奇数,同时是 s^2/s=s ,所以s是一个正奇数,这就是最简单的说明s是奇数的办法。
比如说最简单的 s=3 ,其对应了占据数 \nu=1/3 ,其有电荷 -e/3 ,这就是传说中的分数电荷。

