大物学习笔记(二十三)——光栅衍射
目录:
- 平面衍射光栅: 由大量等缝宽、等缝间距的平行狭缝所构成的光学元件。
- 光栅常量: d=b+b'=a+b (这是教科书的两个表示派系。第一个b来表示小缝宽度,b'来表示小缝间距。第二个a来表示小缝宽度,b来表示小缝间距。)
- 光栅方程(明纹): dsin\varphi=\pm k \lambda , k=0,1,2...
- 暗纹: dsin\varphi=\pm (k+\frac{n}{N}) \lambda , k=0,1,2... , n=1,2... (N是光栅缝总数)
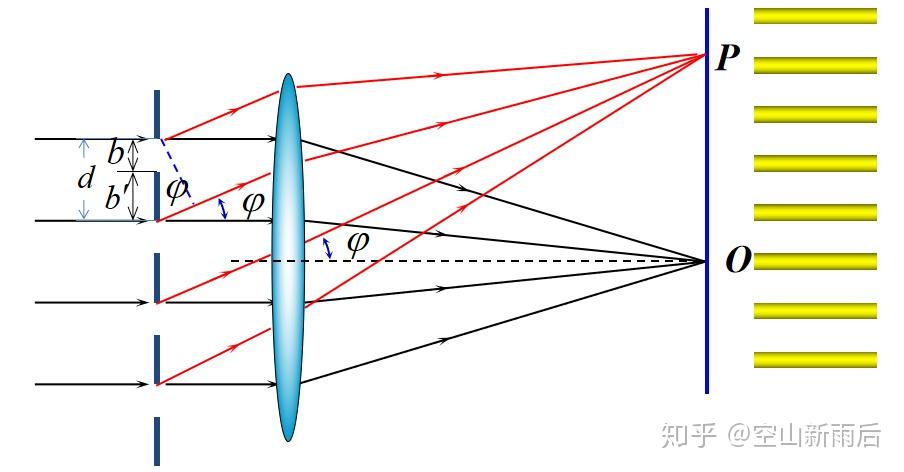
每一个小缝隙都是刚刚的单缝衍射一样的。但是这里最大的光程差变了,最大光程差是第一个小缝的上部到第二个小缝的上部。而整个光栅,不管他有多少个小缝,总是这样子的重复。所以到达P点的光就是N个这个小区间的光干涉增加。但是这时候引入了一个问题,如果这个小区间的光本身就干涉减弱了呢,那么0的干涉相加不还是0。对的,所以,此时多了一个缺级。也就是这个区间干涉出来的光,本身就干涉减弱了,那再干涉加强也还是暗纹了。也就是 a sin\varphi=k'\lambda 的时候。代入光栅方程,就解得如下的式子。
- 缺级: k=k'\frac{d}{a} , k’=1,2,3...
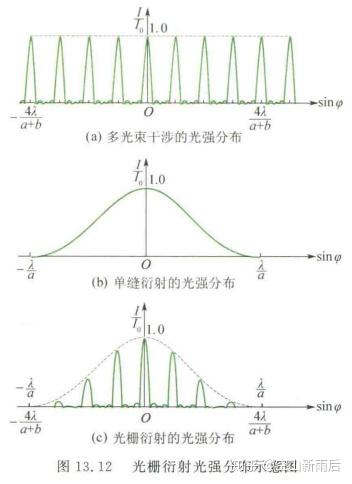
不同的干涉、衍射的光强分布:
前面都是讨论的垂直入射的情况,如果入射不是垂直的,那就再多加在经过缝隙之前的光程差。

- 倾斜入射的光栅公式: d(sin\varphi \pm sin\theta)=\pm k\lambda , k=0,1,2...
- 图中的虚线就是光栅,实线是光栅平面的法线。 \theta 是入射光线与法线的夹角, \varphi 是衍射之后的光线与法线的夹角。 如果 \theta、\varphi 在法线的同一侧,如上图a,就是取加号。反之取减号。
- 光栅光谱:

如图所示,不同颜色的光因为波长不同,他们衍射出来的位置也都是不同的。最后不同波长的光就分散开来,形成了一个光带。因为很多晶体的规则排列就可以当做是光栅,测得晶体的衍射光谱,也就可以反推出晶体结构等。
- 光栅衍射k的最大取值: k=\frac{d}{\lambda} 。(衍射角最大肯定只能取到 \frac{\pi}{2} ,所以最多就只有这么多。如果板不是无限大的话,那就在计算一下板对应的最大衍射角是多少。)
例题
1.


(像这里的第一问,如果考试不能用计算器,然后反三角你也算不出来,你就把反三角的表达式写在那里,你前面算对了,他也不能说你错了。)
2.


(所有图片均来自网络,侵删)


