数学建模预测模型实例（一）---大学生体测数据模型原创

本篇文章中，假设获取到了某大学两个年级共1000人的大学生体质健康测试的每项测试成绩及总分，测试项目包括：身高，体重，肺活量，50m，1000/800，引体向上/仰卧起坐，坐位体前屈。目的是通过前期数据挖掘探索性数据分析等建立大学生体测成绩预测模型，进而在模型里添加天气（温度、湿度、风速）影响因子，模拟得出天气因素对于体测成绩的具体影响程度。
数据分析基本过程包括：获取数据、数据清洗、构建模型、数据可视化以及天气影响下的体测成绩的变化趋势的分析。
数据是存在Excel中的，可以使用pandas的Excel文件读取函数将数据读取到内存中
获取数据：预处理data无缺失值提取密码：rkti
导入原始数据

#导入原始数据
import numpy as np
import pandas as pd
x_pre=[]
excel_path = r'C:\Users\15643\Desktop\公众号\体测-大学之殇\预处理data无缺失值.xlsx'
df = pd.DataFrame(pd.read_excel(excel_path))
# 把年级信息换成年龄 2018=20 2019=19
df['年龄'] = df['年龄'].apply(lambda x :20 if x == 2018 else 19)
# 把性别信息换成 男=1 ;女=2 
df['性别']=df['性别'].apply(lambda x:1 if x == '男' else 2)
缺失值处理
 
由于此次原始数据是没有缺失值的，所以这里就大概介绍一种缺失值填补算法：使用KNN算法进行缺失值的填补。 
作为一种机器学习算法，KNN使用k个最近的观察值（根据某种距离度量的方法计算出来的）来预测缺失值。通俗来说就是根据其他特征找到与缺失值最相近的k个特征点，再进行平均求值。 
在像本案例这样的小数据集中KNN算法是非常有用的，因为计算量较小；因此大数据集一般不建议采用KNN算法填补缺失值。 
我们引入了一个带有一些缺失值的数据集，并且运用knn算法预测缺失值 
#数据表中的缺失值用KNN算法来预测,男女分开进行预测
import numpy as np
from fancyimpute import KNN
#回归问题，往往预测的是某种属性的值。则统计这k个样本点的该属性值，并对其求平均值。然后将得到的平均值赋予为目标点的属性取值。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()#z-score 标准化 标准差标准化的方法使得把特征值映射到均值为0，标准差为1的正态分布
#male
std_df_male = scaler.fit_transform(df.loc[df['性别']==1])
filled_knn_male = KNN(k=5).fit_transform(std_df_male)#利用knn填补缺失值
data_complete_male = pd.DataFrame(filled_knn_male)#保存结果 
#female
std_df_female = scaler.fit_transform(df.loc[df['性别']==2])
filled_knn_female = KNN(k=5).fit_transform(std_df_female)#利用knn填补缺失值
data_complete_female = pd.DataFrame(filled_knn_female)#保存结果    
#concat将男女数据表连接成一个表
data_complete=pd.concat([data_complete_female,data_complete_male])
探索性数据分析–数据分布直方图
 
首先做出每一项特征的分布直方图 
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
std_df = scaler.fit_transform(df)
std_df = pd.DataFrame(std_df)
std_df.columns=['年龄','性别','身高','体重','肺活量','50m','1000/800','坐位体前屈','立定跳远','引仰','总分']
std_df_male = std_df.loc[std_df['性别']<0]
std_df_female = std_df.loc[std_df['性别']>0]
import matplotlib.pyplot as plt# 可视化
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
%pylab inline
def draw(data):
    data.hist(figsize=(16,14),grid=False,)
    plt.savefig(r'C:\Users\15643\Desktop\公众号\体测-大学之殇\data.jpg')
    plt.show()
draw(std_df)

 从这里我们可以大致观察一下所获取到的数据是一个性别分布不均衡的数据集，这可能就会对我们之后分性别的体测数据模型的构建造成一定的影响。 
除此之外，我们还可以发现，引体向上/仰卧起坐、坐位体前屈、肺活量、身高等的分布较为离散，我们可以进一步假设他们对于总分的影响因素可能较大。 
探索性数据分析–相关性热力图的绘制
 
为了进一步证实我们在直方图中的发现，我们绘制了各特征之间皮尔逊系数的相关性热力图（代表两辆特征之间的相关程度） 
import matplotlib.pyplot as plt# 可视化
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
import seaborn as sns
%pylab inline
def draw_heatmap(data):
    ylabels = data.columns.values.tolist()
    df = pd.DataFrame(data)
    dfData = df.corr()#相似度由皮尔逊相关系数度量
    #皮尔逊相关系数——Pearson correlation coefficient，用于度量两个变量之间的相关性，其值介于-1与1之间，值越大则说明相关性越强。
    0.8-1.0     极强相关
    0.6-0.8     强相关
    0.4-0.6     中等程度相关
    0.2-0.4     弱相关
    0.0-0.2     极弱相关或无相关
    plt.subplots(figsize=(15, 10)) # 设置画面大小
    sns.heatmap(dfData, annot=True, vmax=1, square=True,yticklabels=ylabels,xticklabels=ylabels, cmap="RdBu")
    plt.show()
draw_heatmap(std_df_male)

 上图为男生体测数据的相关性热力图，从中我们可以很轻易的发现，引体向上，1000m，50m这些普遍意义上比较令人痛苦的项目的确与体测能拿多少分挂钩；而我们基于直方图的观察则是过于片面了。 
女生的情况也相差无几，以下可以看出这一点。
  
构建大学生体测成绩预测模型
 
基于刚刚的探索性数据分析，我们决定以1000/800m、50m、立定跳远、引体向上/仰卧起坐这四个较强相关性的测试项目的成绩去预测体测总分的成绩。 
以上四项测试包含了弹跳力，爆发力，身体协调性，耐力，并且也有手部，腿部，腰腹背部力量的训练过程。可以说是基本囊括了所有的体育测试训练的方面。所以我们确信我们选择的这四项测试可以很好的代表体测。 
模型的确定
 
由于我们的模型为预测模型，因此我们考虑机器学习中最简单的有监督学习算法–线性回归。而我们选取的用来拟合总分数据的特征有四个，所以我们就考虑一个非线性关系的建模。 
为了将这一个非线性模型转换为线性模型，我们就需要在模型中纳入多项式特征，以创建多项式回归模型。 
简单来说就是在阶数=k的情况下将每一个特征转换为一个k阶的多项式，这些多项式共同构成了一个矩阵，将这个矩阵看作一个特征，由此多项式回归模型就转变成了简单的线性回归。 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.




    
preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression,Perceptron
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import train_test_split
target = std_df_female['总分']
data_complete_ = std_df_female.loc[:,['50m','1000/800','立定跳远','引仰']]
x_train, x_test, y_train, y_test = train_test_split(data_complete_,target, test_size=0.3)
rmses = []
degrees = np.arange(1, 10)
min_rmse, min_deg,score = 1e10, 0 ,0
for deg in degrees:
	# 生成多项式特征集(如根据degree=3 ,生成 [[x,x**2,x**3]] )
	poly = PolynomialFeatures(degree=deg, include_bias=False)
	x_train_poly = poly.fit_transform(x_train)
	# 多项式拟合
	poly_reg = LinearRegression()
	poly_reg.fit(x_train_poly, y_train)
	#print(poly_reg.coef_,poly_reg.intercept_) #系数及常数
	# 测试集比较
	x_test_poly = poly.fit_transform(x_test)
	y_test_pred = poly_reg.predict(x_test_poly)
	#mean_squared_error(y_true, y_pred) #均方误差回归损失,越小越好。
	poly_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred))
	rmses.append(poly_rmse)
	# r2 范围[0，1]，R2越接近1拟合越好。
	r2score = r2_score(y_test, y_test_pred)
	# degree交叉验证
	if min_rmse > poly_rmse:
		min_rmse = poly_rmse
		min_deg = deg
		score = r2score
	print('degree = %s, RMSE = %.2f ,r2_score = %.2f' % (deg, poly_rmse,r2score))
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(degrees, rmses)
ax.set_yscale('log')
ax.set_xlabel('Degree')
ax.set_ylabel('RMSE')
ax.set_title('Best degree = %s, RMSE = %.2f, r2_score = %.2f' %(min_deg, min_rmse,score))  
plt.show()

 这里同样是以男生体测数据作为例子，我们可以得出二阶多项式回归模型是最佳的模型。 
构建二阶多项式回归模型
 
我们以二阶构建多项式回归模型 
#scikit-learn 多项式拟合(多元多项式回归)
#PolynomialFeatures和linear_model的组合 (线性拟合非线性)
#[x1,x2,x3]==[[1,x1,x1**2],[1,x2,x2**2],[1,x3,x3**2]]
########
#male
########
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression,Perceptron
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import train_test_split
target = std_df_female['总分']
data_complete_ = std_df_female.loc[:,['1000/800','50m','立定跳远','引仰']]
x_train, x_test, y_train, y_test = train_test_split(data_complete_,target, test_size=0.3)
# 多项式拟合
poly_reg  =PolynomialFeatures(degree=2)
x_train_poly = poly_reg.fit_transform(x_train)
model = LinearRegression()
model.fit(x_train_poly, y_train)
#print(poly_reg.coef_,poly_reg.intercept_) #系数及常数
# 测试集比较
x_test_poly = poly_reg.fit_transform(x_test)
y_test_pred = model.predict(x_test_poly)
#mean_squared_error(y_true, y_pred) #均方误差回归损失,越小越好。
mse = np.sqrt(mean_squared_error(y_test, y_test_pred))
# r2 范围[0，1]，R2越接近1拟合越好。
r2 = r2_score(y_test, y_test_pred)
print(r2)
以下为分别构建的男女体测成绩预测模型的解释率
  
构建天气因素对于体测成绩的具体影响程度模型
 
在完成构建体测成绩预测模型之后，我们便着手于探索天气因素对于长跑成绩乃至于对于整个体测成绩的影响。 
确定模型思路
 
由于我们有的数据集中不存在天气影响因素这一特征，也就是说这一次的模型构建是在没有数据的基础上进行的。因此首先我们进行了文献查阅。 
根据以下文献我们得知了人的冷热感取决于多种因素的共同影响，而气象学中的风冷指数以及不适指数可以很好的量化这些影响，因此我们选定了这两个气象学指标作为长跑时的影响因素。这两个指标是由风速，湿度，温度来进行表示的，也符合大众对于天气影响因素的认知。 
 武雪莲.气象条件对马拉松成绩影响的研究[J].中国体育科技,2012,48(05):16-20. 
建立数学模型
 
根据普适的观念我们姑且认为风冷指数和不适指数都是会给长跑带来一定不利影响的（风大跑不快，太冷跑不快），而大风天带来的影响是要多于温度带来的影响的，所以我们在这里设置权重，风冷指数的权重为0.7，不适指数的权重为0.3，而且由于两个指数带来的影响是两方面的，所以我们选择把这种影响进行加和，得到以下方程。
 
 （Ko为风冷指数，Ic为不适指数，ta为温度，RH为湿度，v为风速，t为未受干扰的跑步时间） 
拟合真实数据
 
在建立好数学模型之后，为模拟出真实情况下长跑成绩可能受到的影响，我们选择用采用蒙特卡洛模拟来连接真实数据与理论模型。 
蒙特卡洛模拟是一种输入一系列随机数反复评估确定性模型的方法。简单来说就是通过一系列随机试验得出结果。 
在此次案例中我们分别选取了一位平均水平的男生和女生，让他们在不同的天气下分别进行一千次随机测试，再进行数据统计。 
我们设定的随机试验的条件是风速介于0级到6级大风（6级大风就是我们生活中遇到的较强的风力了），湿度介于0到100%，温度是0到20度（模拟体测那段时间北京的温度） 
###蒙特卡洛模拟
###准备阶段
#####
#male
#####
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#找出一个均值男生
df_800 = df['1000/800']
df_800_mean = df_800.mean()
df_50 = std_df_male['50m'].mean()
df_tiaoyuan = std_df_male['立定跳远'].mean()
df_yinyang = std_df_male['引仰'].mean()
df_1000_male =  std_df_male['1000/800'].mean()
#ta 空气温度 RH相对湿度 v风速
##ta:0~20 RH：0~1 风速0~13.8（6级大风）
ta_list=[]
RH_list=[]
v_list=[]
y=[]
#数学模型建立
def generateequ(ta,RH,v):
    ko = (v*50+10.45-v)*(33-ta)#风冷指数
    ic = ta*1.8+32-0.55*(1-RH*0.01)#不适指数
    equ = ko*0.001*0.7+ic*0.001*0.3 #将两个指数同除以1000将其对于长跑的影响范围限定为0-20秒
    if equ <0:
        return df_800_mean
    else:
        return equ +  df_800_mean
#蒙特卡洛模拟开始，1000次随机模拟   
for i in range(1,1000):
    ta=np.random.uniform(0,20)
    RH=np.random.uniform(0,1)
    v= np.random.uniform(0,13.8)
    equs = generateequ(ta,RH,v)
    y.append(equs)
    ta_list.append(ta)
    RH_list.append(RH)
    v_list.append(v)
y = np.array(y)
y_ =pd.DataFrame(y)
#将模拟后的长跑成绩进行标准化处理，方便之后模型拟合
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
yd_df = scaler.fit_transform(y_)
yd_df_ = pd.DataFrame(yd_df)
#1000次蒙特卡洛模拟后的长跑成绩并入平均男生的数据中
df1 = np.ones(len(yd_df_))
yd_df_['50m']=pd.DataFrame(df1)
yd_df_['50m'] =yd_df_['50m'] .apply(lambda x :df_50 if x == 1 else 0)
df2 = np.ones(len(yd_df_))
yd_df_['立定跳远']=pd.DataFrame(df2)
yd_df_['立定跳远'] =yd_df_['立定跳远'] .apply(lambda x :df_tiaoyuan if x == 1 else 0)
df3 = np.ones(len(yd_df_))
yd_df_['引仰']=pd.DataFrame(df3)
yd_df_['引仰'] =yd_df_['引仰'] .apply(lambda x :df_yinyang if x == 1 else 0) 
可视化结果
 
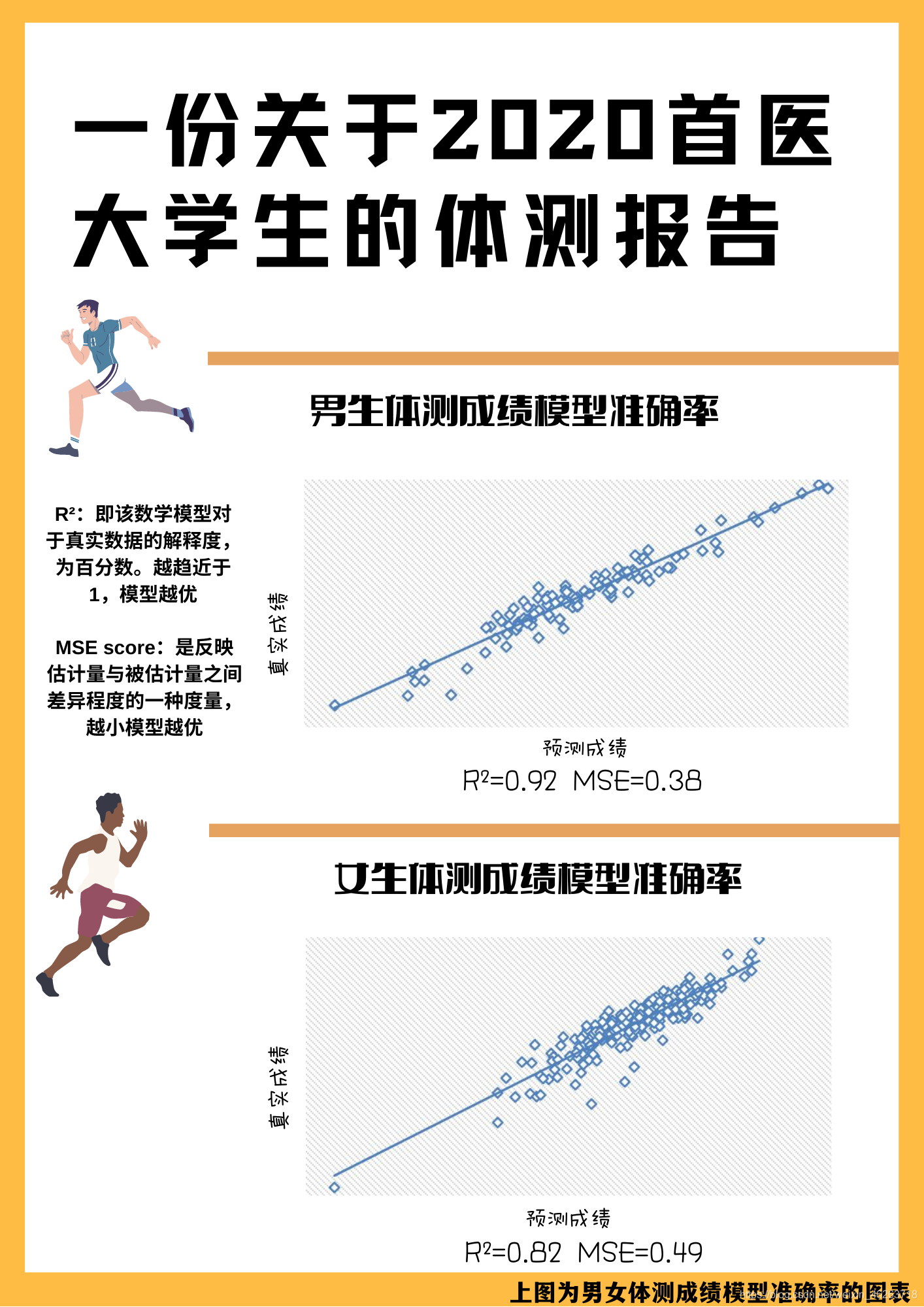
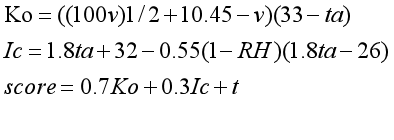在建立了完整的天气影响模型之后我们首先找到了男女生体测的最适天气因素（总成绩最高的） 
#得到最适三个参数（对总成绩影响最小）
#ta 空气温度 RH相对湿度 v风速
x_poly = poly_reg.fit_transform(yd_df_)
y_pred = model.predict(x_poly)
par_best=[]
y_best=[]
for i in range(len(y_pred)):
    if y_pred[i]==y_pred.max():
        x_v_i=v_list[i]
        x_RH_i=RH_list[i]
        x_ta_i=ta_list[i]
        par_best.append([x_v_i,x_RH_i,x_ta_i])
        y_best.append(y[i])
par_best#得到最适三个参数（对800成绩影响最小）

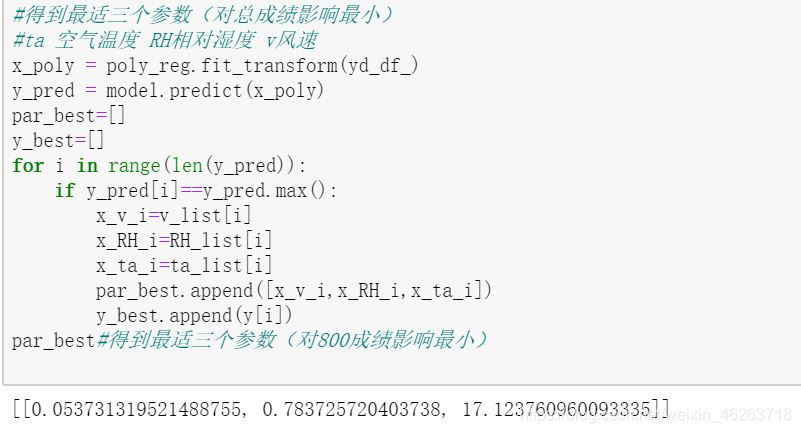
 从这里我们看出最适天气因素是无风，凉爽的天气，这也符合我们的普适认知。 
随后我们统计了在0~3级微风，4-5级和风，5-6级劲风的天气条件下在这1000次随机试验中长跑平均多花的时间。通过调整蒙特卡洛模拟中温度、湿度，风速等随机取样的范围实现。
  
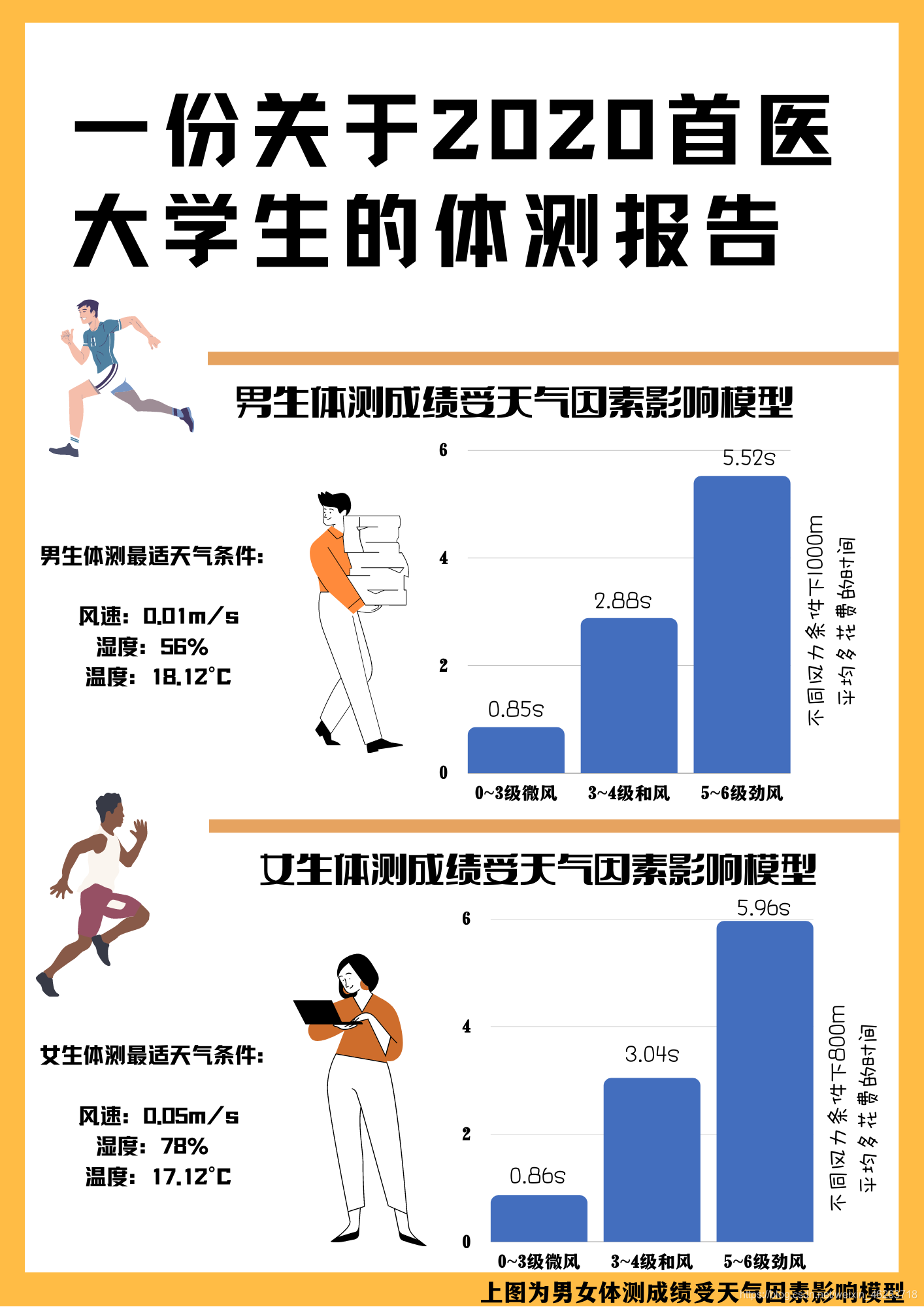
结论：我们发现和大多数人想的一样，适宜跑步的天气是凉爽湿润且无风的好天气，在这种天气体测身心愉悦，可以发挥得更好。 
而相比较而言的大风天也是真的很夺命，大风给长跑带来的不仅仅是在跑步的我们的生理上的痛苦，还有成绩上的下滑！ 
但是大家可以松一口气的是，基于我们的模型而言，大风对于长跑的影响是在6s以内的，所以大风并不能阻挡任何人奔向体测的及格线，只不过就是会比平常更加的难受罢了。 
喜欢这篇数学建模案例的话，欢迎关注我们和我们一起交流！
 奇趣多多，数模多多！
 
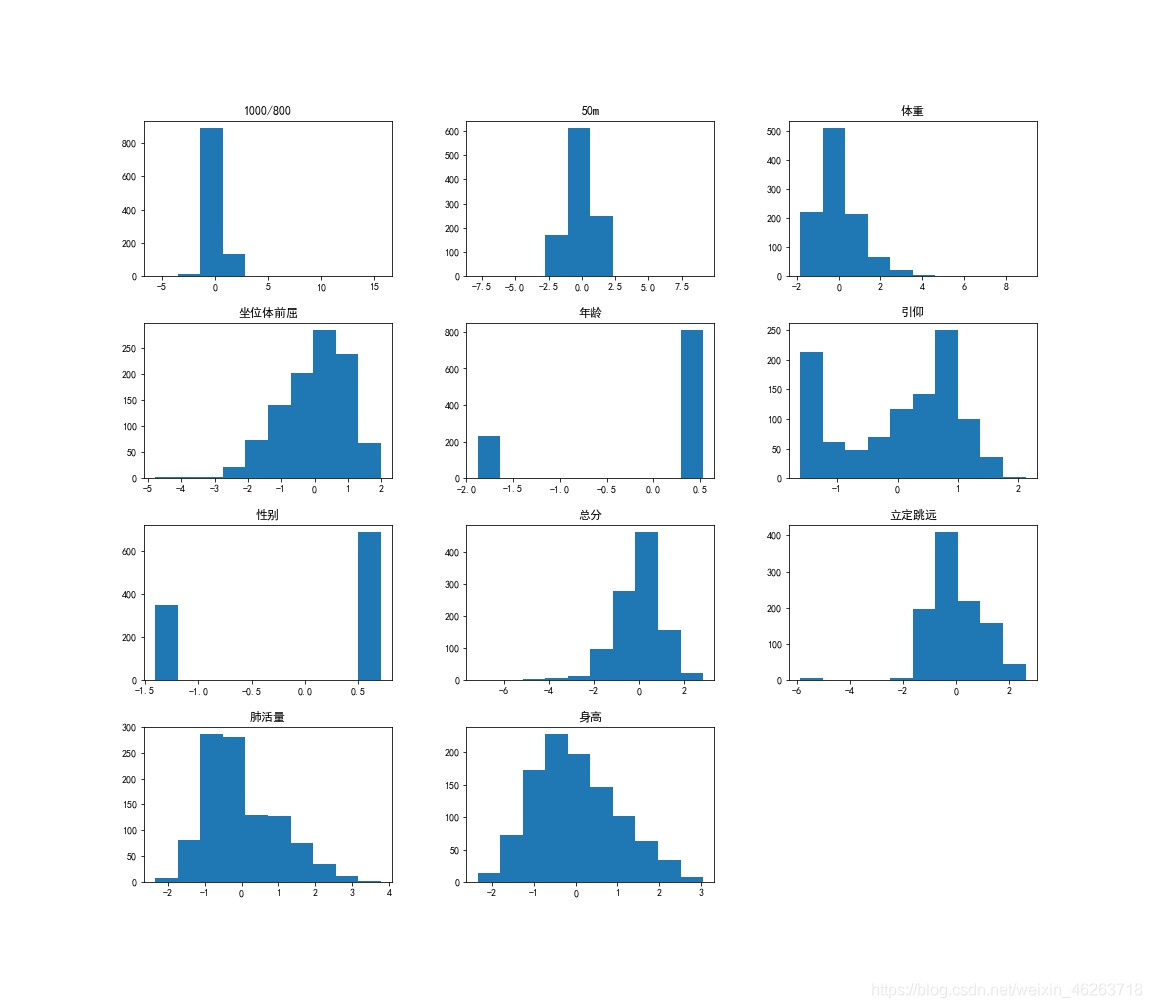
                    数学建模预测模型实例–大学生体测数据模型建立模型的目的本篇文章中，假设获取到了某大学两个年级共1000人的大学生体质健康测试的每项测试成绩及总分，测试项目包括：身高，体重，肺活量，50m，1000/800，引体向上/仰卧起坐，坐位体前屈。目的是通过前期数据挖掘探索性数据分析等建立大学生体测成绩预测模型，进而在模型里添加天气（温度、湿度、风速）影响因子，模拟得出天气因素对于体测成绩的具体影响程度。数据分析基本过程包括：获取数据、数据清洗、构建模型、数据可视化以及天气影响下的体测成绩的变化趋势的分析。数
				数学建模是对现实世界的特定对象，为了特定的目的，根据特有的内在规律，对其
进行必要的抽象、归纳、假设和简化，运用适当的数学工具建立的一个数学结构。数学
建模就是运用数学的思想方法、数学的语言去近似地刻画一个实际研究对象，构建一座
沟通现实世界与数学世界的桥梁，并以计算机为工具应用现代计算技术达到解决各种实
际问题的目的。建立一个数学模型的全过程称为数学建模。因此“数学建模”（或数学
实验）课程教学对于开发学生的创新意识，提升人的数学素养，培养学生创造性地应用
数学工具解决实际问题的能力，有着独特的功能
				MATLAB—常用数学建模算法大全（26种）：理论介绍+源代码+实例分析
1.    全国大学生数学建模比赛介绍及其入门（国赛+美赛）
2.    使用MATLAB进行灰色预测 GM（1，1）
3.    使用MATLAB进行多元线性回归预测
4.    使用MATLAB进行BP神经网络数值预测
5.    MATLAB-自定义函数拟合（lsqcurvefit）
6.    MATLAB: 0-1规划（背包问题）
7.    MATLAB-线性规划求最优解
8.    MATLAB-随机森林实现数据回归分析预测
9.    MATLAB-GM（1，N）灰色预测模型的建立
10.  MATLAB-偏最小二乘回归分析
11.  MATLAB-基于灰色神经网络的预测算法研究（订单需求预测）
12.  MATLAB-遗传算法-求解多元非线性规划问题
13.  MATLAB-综合评价与决策（数学建模）
14.  MATLAB-模拟退火算法
15.  MATLAB-主成分分析法CCC 
16.  MATLAB-多目标线性规划问题
17.  MATLAB-熵权法
由于字数限制，其它算法见压缩包。
				毕业设计基于VUE的学生体测管理系统项目源码，也可作为期末大作业。
老师 ry admin123 刘三国 123456 管理员 manager 123456 学生 20220102 123456
使用教程如下：
# 进入项目目录
cd ruoyi-ui
# 安装依赖
npm install
# 建议不要直接使用 cnpm 安装依赖，会有各种诡异的 bug。可以通过如下操作解决 npm 下载速度慢的问题
npm install --registry=https://registry.npm.taobao.org
# 启动服务
npm run dev
浏览器访问 ..
# 构建测试环境
npm run build:stage
# 构建生产环境
npm run build:prod
【内容简介】
本书将应用数学的基本理论、实例、应用数学软件有机地结合成一体,既简要介绍一些最常用的解决实际问题的应用数学知识，又联系实际介绍应用相应的数学知识建立数学模型，并用合适的数学软件包来求解模型在大多数章的最后一节。结合相应知识和软件包介绍一个大型的数学建模案例，这些案例主要取材于最近几年全国大学生数学建模竞赛题.
第1章 线性规划 
1．1 线性规划模型 
1．2 单纯型算法 
1．3 对偶单纯型算法 
1．4 灵敏度分析及影子价格 
1．5 用MATLAB优化工具箱解线性规划 
1．6 习题 
第2章 整数线性规划 
2．1 割平面法 
2．2 分枝定界法 
2．3 习题 
第3章 无约束优化 
3．1 数学预备知识 
3．2 无约束最优化问题的解 
3. 3 用MATLAB优化工具箱解无约束最优化 
3．4 习题 
第4章 非线性规划 
4．1 非线性规划的数学模型 等等
				双色球概率预测模型
最近新晋彩民佩瑞对于双色球产生了极为浓厚的兴趣，在买过几注随机号码中奖无果后，决心潜心修炼，钻研一个比较靠谱的预测方法！所以有了这篇文章，文章思路及结果仅供娱乐，请勿当真！
在产生这个想法之后我首先查阅了网络上各种各样的双色球预测模型，发现了几类具有代表性的：
1.基于神经网络的回归预测模型
2.基于LSTM的预测模型
3.基于深度学习的预测模型
看到这三种预测模型是不是觉得很高深，没错！我也是这样的感觉！所以我又开始了新一轮的资料搜索，这次去详细的了解了一下有关双色球的