特别诺贝尔奖获奖论文《天赋与运气-随机性在成功和失败中的作用》
西江月·世事短如春梦
【作者】朱敦儒 【朝代】宋
世事短如春梦,人情薄似秋云。不须计较苦劳心。万事原来有命。幸遇三杯酒好,况逢一朵花新。片时欢笑且相亲。明日阴晴未定。
从1991年开始以来,搞笑诺贝尔奖的名气逐渐增大,大约在 2009年的时候,中文世界开始有系统的报道。那些荣获搞笑诺贝尔奖的奖项最初是科学家用来自嘲的,其中有些从内容上看就是很不堪的。比如1993年,搞笑诺贝尔生理学或医学奖颁给了一篇只有9页的论文,但因为有976个人署名,结果署名页竟然有4页之多。同时,这些奖项里也有一些非常有灵气的研究,甚至一些获奖人后来还获得了真正的诺贝尔奖。2022年这一届的搞笑诺贝尔经济学奖颁发给了一项研究,它的标题是《天赋与运气,随机性在成功和失败中的作用》。这个研究建立了一个模型,分析了运气对个人的成功有多大的作用。
1
模型设计
研究的背景是一个现代社会的悖论:
在各种文化中,人们总是把成功归结为个人的努力、天赋、优秀的品质和高超的技能,但那些成功者里有很多在成功之前其实就是平庸之辈,所以我们必须承认运气在成功中起了作用。但是,运气占比多大呢?
天赋、技能等等如果可以用数值去衡量的话,大致趋于正态分布。 也就是说,大部分在这些项目上处于均值附近,正负两个标准差之内,极少部分天赋异禀。
比如20岁男性100米跑,大部分人的成绩都在13-19秒之间,就算你是百年不遇的奇才,也只是9.6秒,比那些平时不太运动的软脚虾快1倍就不得了了。
努力程度也是这样。你每天投入学习的时间撑死了就 15个小时,不能再多了,而那些跟着教学进度走、浑浑噩噩的学生,每天也至少有7个多小时在学习,最好最差也只差了1倍。
但成功如果用财富来衡量,成功度差的可就远不止1倍了,最好和最差可能有上百亿倍的区别。这是因为财富的分布按幂率呈现。
今天,很多银行对客户存款的统计就发现,2%的人拥有80%的财富。如果你缩小观察区间,只看这2%的最富有的人的财富状况的话,其实也依然满足富人中最富有的2%的人拥有那80%财富的80%。这就是幂率。
幂率的存在提醒了我们, 对于一个人的一生来说,可获取的财富总量几乎是无限大的,机会是很多的。
于是,意大利卡塔尼亚大学经济系和物理系就联合做了一个模型,量化的看看一个人的一生里,靠天赋获取的财富多,还是靠运气获取的财富多。

在一个 201×201的正方形里,随机分布1000个小人,它们代表了芸芸众生。每人初始时手里有10块钱,每一个小人有一个预设的天赋值,天赋值的高低是按正态分布的。
在这张图里,还随机洒下500个点,这些点有绿色的,也有红色的,绿色代表好事,红色代表坏事。
如果洒下的绿点正好和随机分布的某个小人重合,就说明好事降临,此人的财富将有机会乘以2,翻倍的几率和此人自带的天赋属性成正比。
同样的,如果随机洒下的红点正好和某个小人重合,就说明坏事降临,他的财富将有一定的几率减半,这个几率和此人自带的天赋成反比,也就是天赋越高,遇到不幸的事情后财富减半的几率越小。
模型运行起来还有一个时间线,就是反复撒点80次,每一次代表6个月,80次就代表经历了40年时间。这有点儿像一个人从20岁走入社会到60岁退休,中间工作的40年时间。
2
运气大于天赋北通按:天赋其实也在运气当中,在八字命理当中。
在好事和坏事各占50%的情况下,每次洒下500个事件,1000个人,初始时每人手里都是 10 块钱,洒了80轮后,结果如下:
只有4个人的资产超过了500块钱。1000个人中,资产最多的20个人拥有全部资产的 44%,大约一半的人手中的资产不足10块钱。这个分布和今天社会中的财富分布高度类似。
再看那个最富有的人,手里一共2560块钱。他的天赋值是多少呢?从高到低,在 1000个人中排名第496,就是个寻常人嘛。
再看天赋排名最高的那个人,他手中的财富是几块钱呢?0.625元,不到1块钱。你还记得吗?最初大家手里都是有10块钱的。
在这个统计中,最穷的人到了60岁,手里就只有0.0006 块钱了。而这个可怜人的天赋值在1000人中排名第80,但他是最穷的人。
这次模拟的结果有点偶然性,那个天赋最高的人差不多也算最穷的了。不过,如果把所有天赋高于均值的人的财富平均一下看,他们经过40年的打拼,财富均值大约是20块钱,从10块钱增到20块钱,中间这10块钱的增长可以视为天赋起到的作用。
但是从10块钱增值到2560块钱,这中间2550块钱的差距可以视为运气所起的作用。10比2550,就是天赋和运气的影响比例。
我们注意,以上只进行了一次模拟。你可能会质疑,那些天赋异禀的家伙此生偏巧非常不走运才这么贫穷,那个资质如此平庸的最富有的人也只是运气而已。
没关系。第二组实验里,让这1000个小人重复了100次人生。这次多了一个假设,每一轮新的人生开始时,这个小人的天赋值会重新设定。
设定多高呢?由他在上一轮中获得的财富来决定,财富越高,天赋在正态分布中也就越靠前。这个设定也符合现实世界的一些特点。
当一个人财富比较多的时候,他能吸引到的异性的综合素质起码从统计角度看也会更好,也自然会在各方面天赋上有更大概率高于那些资源非常少的人。
这样的话,他们下一代的天赋应该相应的增加一些,于是就做了这样的假设。
在100代之后,结果是这样的:
最富有的个体手里有40960块钱,这个人的天赋值在1000人中排名480名,完全是个标准的平庸之辈。再看天赋最高的那个人,手中有2560块钱,这个数字虽然也还不错,但只有最富有的人的6%。
如果天赋是成功的全部原因,那么千里挑一的天赋应该正好对应到千里挑一的财富,也就是4万多块钱。
但实际上,千里挑一的天赋只换得那个财富值的6%。这就是更大规模假设后天赋在成功中的作用。
如果再看这100轮中,每轮结束后,天赋最高的人获得最富有的人的称号的概率呢?3%。
还有一个更加令人遗憾的结果,运行了100轮之后,1000个人中最有天赋的160个人里,手中的钱大于初始资金10块钱的概率是32%。
我们不禁要问,为什么?天赋很好的人忙活了一辈子都有2/3的人手里的钱比初始值更少,这不是白忙活了吗?
其实,我们不能把这个结果当作真实的人生。生活中的财富变化往往是加减法,而不是以乘以2或者除以2的形式进行的。
这个模型只是告诉我们,面对时间和空间上巨额分布的财富机会,运气远比天赋更加重要。
而另一个更加重要的事实是, 人群的财富分配不可避免的呈现幂率分布,绝大部分人没钱,极少数人富有到无以复加的地步。 这是自然规律。
3
社会秩序与个人成功
此外,这个研究还设置了其他数值,就是好事和坏事出现的比例。之前不是各 50%吗?研究人员还试了试好事80%、坏事20%和坏事80%、好事20%的情况。结果也很有意思:
当80%都是好事的情况下,天赋越高的人获得越多财富的机会就越大。这其实更接近于我们期待的结果,觉得更公平。
而反过来,当坏事占80%的时候,天赋高低和获得财富的多少的关系就非常微弱了,几乎就是运气决定了一切。
而且在坏事占比80%的情况下,最富有的人和最穷的人之间的财富差距也大大缩减,看上去好像是一个更加平均的社会,但实际上,在坏事占比80%的时候,1000个人里,只有87个人在忙活了一辈子之后,手里的钱比初始值更多。
这个研究映照出很多种不同的社会——
在那些秩序良好、人们积极向上、偶发事件大都是好事的社会,天赋高的人相对更容易获得巨大的成功,而这种巨大的成功也会导致巨大的贫富差距。
而在一天一个坑、两天一个雷的秩序洼地,一个人天赋的高低和他是否成功几乎没有关系,而这样的社会尽管贫富差距小很多,却是极度贫穷的。
北通按:所谓社会秩序的不同,即是命理中所谓“风土不及”。
虽说是搞笑诺贝尔奖,但确实是严谨的社会学研究,评委也都是货真价实的科学家。只能说无论中西,偏向玄学领域的研究毕竟难登大雅之堂。所以冠以“搞笑诺贝尔奖”的名头。只能期待科学的尽头是玄学那一天的尽早到来。
英文论文原文翻译:
高度竞争激烈的西方文化的主导精英范式是基于这样一种信念,即成功,如果不是完全是因为个人 品质,如才能、智力、技能、聪明、任性、任性、努力工作或冒险。有时,我们愿意承认,一定程 度的运气也可以在取得重大成功方面发挥作用。但是,事实上,人们经常低估外部力量在个人成功 故事中的重要性。众所周知,情报 (或者更一般的来说,人才和个人素质) 展品人口高斯分布,而 财富的分布——通常被认为是成功的代理遵循通常幂律 (帕累托法) ,绝大多数的穷人和非常少量 的亿万富翁。这种差异在输入的正态分布之间,与一个典型的尺度( 一般的人才或智力) 以及输出的规模不变的分布,表明了一些隐藏的因素在幕后起作用。在本 文中,我们认为这种成分只是随机性。特别是,我们简单的基于代理的模型表明,如果生活中的成 功确实需要一定程度的才能,那么最有才华的人几乎永远不会达到成功的顶峰,被平均有才华但明 显更幸运的人所超越。据我们所知,这个违反直觉的结果——尽管在大量文献中含蓄地暗示着—— ¯在这里第一次被引用。它新地揭示了在已达到的成功水平的基础上评估绩效的有效性,并强调了 给那些最终可能比其他人更幸运的人分配过多的荣誉或资源的风险。我们还比较了几个政策假设, 以显示最有效的公共研究资助的策略, 旨在提高精英管理、思想的多样性和创新能力。
1 . 介绍
幂律分布在许多物理、生物或社会经济复杂系统中的普遍存在可以看作是它们强相关 的动态行为及其尺度不变的拓扑结构[1 –4]的一种数学特征。在社会经济背景下,在 帕累托的著作[5 –9]之后,众所周知,财富分配遵循幂律,其典型的长尾形状反映了 我们社会中深深存在的贫富差距。 [10]最近的一份报告显示,今天的这一差距远远比 人们所担心的要大:8个人拥有与人类最贫穷的36亿人拥有同样的财富。在过去的20年 里,一些理论模型被发展到在统计物理学和概率论的背景下推导出财富分布,通常采 用具有简单的潜在动力学的多主体视角[11] – 1 6 ] .
沿着这条线,如果一个人认为个人财富作为成功的代理,可以认为其深度不对称和 不平等的分布是自然迪®天赋的结果,技能、能力、智力、能力或衡量他们的任性,努 力工作或决心。这样的假设是间接的,在所谓的精英范式的基础:它不仅我们的社会 授予工作机会,名声和荣誉,而且政府采用的策略分配资源和资金给那些被认为是最值得的个人。
然而,先前的结论似乎与上述引用的人类特征和品质在人群中呈正态分布的公认证 据形成了严格的对比。e., 在一个给定的均值周围遵循一个对称的高斯分布。例如, 通过智商测试测量的智力遵循这样的模式:平均智商是100,但没有人的智商是1000或 10000。以工作时间来衡量,工作标准也是如此:有人工作时间比平均时间多,而其他 人少,但没有人工作时间比其他人多10亿倍。
另一方面,现在有越来越多的证据表明,机会、运气,或者更普遍的是随机因素, 在决定我们个人和职业生活中的成功或失败方面的基本作用。特别是,它一直是
表明科学家在他们的职业生涯中也有同样的机会出版他们最热门的[17];那些姓氏首 字母较早的人更有可能获得最高部门[18]职位;学者收集的文献计量指标的分布可能 是与发表或°机制[19]的乘法现象相关的机会和噪音的结果;一个人在按字母顺序排 序的列表中的位置可能对确定获得过度订阅的公共服务[20]很重要;中间名首字母增 强了对智力表现[21]的评价;名字容易被推翻的人比±发音[22]的人更积极;姓氏听 起来高贵的人更经常做经理而不是雇员[23];有男性头衔的女性在法律职业生涯中更 成功[24];全球范围内人员收入差异的大约一半只能用他们的居住国和该国[25]的收 入分配来解释;成为首席执行官的可能性主要取决于你的名字或你的出生月份[26] – 28];这些创新的想法是我们大脑网络[29]中随机行走的结果;甚至是患癌症的可能性 ,也许是一个辉煌的职业生涯,主要是由于简单的坏运气[30,31]。最近关于终生繁殖 成功的研究进一步证实了这些说法,即如果性状的变异可能影响种群的命运,那么运 气往往支配着[32,33]个体的生活。
近年来,许多作者,其中统计学家和风险分析师Taleb [34,35]投资策略师[36]和 经济学家弗兰克[37],探索在几个成功的书探索运气和技能之间的关系¯金融贸易,商 业、体育、艺术、音乐、文学、科学和许多其他¯榆树。他们得出的结论是,偶然事件 在生活中发挥的作用比许多人曾经想象的要大得多。实际上,他们并不认为成功是独 立于人才和工作标准的,因为在竞争激烈的领域或“赢家通吃”的市场,就像我们今 天生活和工作的地方,表现良好的人几乎总是非常有才华和努力工作。简单地说,他 们得出结论认为,天赋和技能是不够的:你也必须在正确的时间出现在正确的地点。 简而言之:运气也很重要,即使它的角色几乎总是被成功人士低估。这是因为随机性 经常以微妙的方式出现,因此很容易构建出将成功描述为不可避免的叙事。塔勒布称 这种倾向\叙事谬误为“[35],而社会学家拉扎斯菲尔德则采用了这个术语\事后偏见 ” 。在他最近的书\一切都是显而易见的:一旦你知道答案”[38],社会学家和网络科 学先驱瓦茨表明叙事谬误和后见之明偏见与特定力量当人们观察异常成功的结果,认 为他们是努力工作和人才的必要产品,而他们主要来自一个复杂的和交织的步骤,每 个取决于先例:如果任何一个是错误,整个职业或生活轨迹几乎
当然,di®也是。这个论点也是基于一个开创性的实验研究的结果,执行几年前由瓦茨 本人与其他作者[39]合作,以前未知的歌曲的成功在艺术音乐市场显示不与歌曲本身 的质量。这显然使任何一种预测都非常狂热,正如最近的另一项研究[40]所显示的那 样。
在本文中,通过采用一种基于代理的统计方法,我们试图现实地量化运气和人才在 成功的职业生涯中的作用。在秒。2、基于最少的假设,i。e., 人才[41]的高斯分布 和成功和失败的乘法动力学[42],我们提出了一个简单的模型,我们称之为\人才与运 气” (TvL) 模型,它模拟了一群人在40年的工作时间内的职业演变。该模型表明,实 际上,随机性在选择最成功的个体中起着重要作用。的确,正如人们所预料的那样, 与装备不足的人相比,有才华的人更有可能在一生中变得富有、出名或重要。但是, 这是一个不那么直观的理由——拥有平均才能水平的普通人注定注定会成功。e.被放 置在一些成功的幂律分配的尾部)比最有才华的人更多,只要他们的一生中更受财富的 祝福。正如[34,35,37]中指出的,这个事实是常见的,但据我们所知,它第一次在这 里被建模和量化。
平均有才华的人的成功强烈地挑战了\精英主义”范式以及所有这些策略和机制, 这些策略和机制给在他们的¯eld[43,44]中被认为最好的人更多的奖励、机会、荣誉、 名声和资源。关键是,在绝大多数情况下,所有对某人的才能的评估都是后验的,只 是通过观察他/她的表现-或达到的结果,在我们社会的某些特定领域,如体育、商业 、¯经济、艺术、科学等。这种误导性的评估最终会转换原因,被评为最有才华的人, 简单地说,最幸运的是[45,46]。符合这一观点,在以前的作品中,它是先进的警告这 样一种\幼稚的精英统治” ,显示了生态的替代策略基于随机选择在许多不同的情况下 ,如管理、政治和¯娘娘腔[47 – 54 ] .在秒。3,我们提供了我们的方法的应用,并概 述了在科学¯c研究背景下可能的公共资金归属方案的比较。我们研究了几种分配策略 的影响,其中包括“精英主义策略” , 目的是探索新的方法来提高社区中最有才华的 人的最低成功水平和由此产生的公共支出的能力。我们还探讨,环境如何影响机会, 如教育和收入水平(® 。e., 外部因素取决于国家和个人来自的社会环境),确实会增加 成功的可能性。最后的结论性结束了论文。
2 . 模型
在接下来的内容中,我们提出了一个基于代理的模型,称为TvL模型,它建立在一组非 常简单的假设之上, 旨在描述一群被幸运或不幸的随机事件影响的人的职业演变。
我们考虑了N个个体,有天赋的个体是Ti (智力、技能、能力等) 正态分布在区间 ½0;1]在一个给定的平均m附近T其标准偏差为aT,随机放置在一个方形世界的¯位置( 见图。具有周期边界条件的1)(i。e., 并被一定的数字N所包围E“移动”的事件 (用 点表示) ,一个幸运的人,其他不幸的人 (模型中不考虑中性事件,因为它们与个人 生活无关) 。在无花果。1,我们用彩色点来报告这些事件:幸运事件,用绿色和相对 百分比pL,和不幸的那些,在红色和与百分比(100 - pL).事件点的总数NE是均匀分布 的,但当然,这样的分布只对N是完全均匀的E! 1 . 在我们的模拟中,通常是NE) N/2 :因此,在每次模拟开始时,幸运或不幸的事件点将随机在世界上的不同地区集中, 而其他地区将更加中立。在方格内的点的进一步随机运动,并没有改变模型的基本特 征,这暴露了一切

图1 . (颜色在线) 为我们的模拟的初始设置的一个例子。本文中提出的所有仿真都是在基于NetLogo代理的 模型环境[55]中实现的。N = 1000个人 (特工) ,具有不同程度的智力 (智力、技能等) ,在具有周期边界 条件的201漏201斑块中随机位于¯的位置。在每次为期几十年的模拟中,它们都暴露在一定数量的N中E幸运 ( 绿色圆圈) 和不幸 (红色圆圈) 的事件,它们沿着随机的轨迹 (随机行走) 在世界各地移动。在这个例子中 ,NE= 500 .
个人在他们的生活中没有大量的幸运或不幸的事件,不管他们自己的才能。
对于单次模拟运行,考虑的工作寿命P为40年 (从20岁到60岁) ,时间步长为6t相 当于六个月。在模拟开始时,所有的代理都被赋予了相同数量的Ci...=Cð0ÞAi = 1;N ,代表他们成功/财富的初始水平。这个选择的目的是不给任何人®任何初始优势。虽 然代理人的人才与时间无关,但代理人的资本却会随时间而变化。在模型的时间演化 过程中,i。e., 在被考虑的代理的生命周期内,所有的事件点都在世界各地随机移动 ,在这样做时,它们可能与某个代理的位置相交。更详细地说,在每次事件点中,每 个事件点在一个随机方向上覆盖两个补丁的距离。我们说,当一个事件点出现在以代 理为中心的半径为1的补丁的圆内时,交点确实会发生 (事件点在交集后不会消失) 。 根据这样的发生,在给定的时间步长t (i。e., 每六个月),对于一个给定的代理®有 三个不同的可能的行动k:
(1)没有事件点截取代理A的位置k:这意味着在过去的六个月里没有发生过相关的事实 ;代理Ak不执行任何操作。
(2)一个幸运的事件拦截了代理A的位置k:这意味着在过去的六个月里发生了一个幸运 事件 (注意,根据[29],一个创新想法的产生也被认为是发生在代理的大脑中的 幸运事件) ;因此,代理ak她的资本/成功加倍,概率与她的天赋成正比k.它将是 Ckðt Þ = 2Ckðt-1Þ仅当rand½0;1] < Tk, i.e., 如果代理足够聪明,从他/她的 运气。
(3)一个不幸的事件拦截了代理A的位置k:这意味着在过去的六个月里发生了一件不幸 的事件;因此,代理ak一半的资本/成功,我。e., Ckðt Þ = Ckðt - 1 Þ /2.
以前的代理的规则 (包括选择初始资本除以2因素,如果不幸的事件,和加倍的选 择,如果幸运的,比例代理的人才) 是故意简单,可以被认为是广泛共享,因为他们 是基于常识证据表明,成功,在每个人的生活,有财产增长或减少非常迅速。此外, 这些规则给有才能的人一个明显的优势,因为他们可以更好地利用运气创造的机会 ( 包括利用他们大脑中产生的好主意的能力) 。另一方面,一场车祸或突然的疾病,总 是一个不幸的事件,人才不起作用。在这方面,我们可以更准确地概括人才的能力, “通过识别任何提高抓住机会的个人素质” 。换句话说,我们所说的“才能” ,泛指 智力、技能、聪明、固执、决心、努力工作、冒险等等。
我们将在下面的文章中看到,拥有伟大人才的优势是获得非常高的成功的必要条件, 但不是必要条件。
. 1 . 2单次运行结果
在本节中,我们将介绍一个典型的单次运行模拟的结果。实际上,这些结果是非常稳 健的,因此,正如我们将在后面展示的,它们可以被认为在很大程度上代表了从我们 的模型中出现的一般框架。
让我们考虑N = 1000代理,开始等量的资本Cð0Þ=10 (无量纲单位) 和一个人才 Ti2½0;1],它遵循均值为m的正态分布T= 0 . 6和标准偏差aT= 0 . 1(见图。2) . 如前 所述,该模拟跨越了P = 40年的现实时间段,通过每个时间段6个月的时间步长演变, 总共有I = 80次迭代。在这个模拟中,我们考虑NE= 500事件点,与一个百分比pL= 50%的幸运事件。
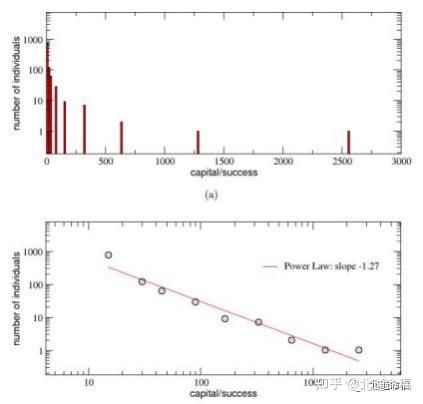
在模拟结束时,如图面板(a)所示。3,我们发现模型的简单动态规则能够产生不平 等的资本/成功分配,有大量的贫穷 (不成功的) 代理和少量的非常丰富 (成功的) 的 代理。在相同¯图的面板(b)中,以对数-对数尺度绘制相同的分布,观察到一个类似帕 累托的幂律分布,其尾部由函数yðCÞ写¯很好地绘制_ 1.27 .因此,尽管人才呈正态分 布,TvL模型似乎能够捕捉到与真实数据比较中观察到的第一个重要特征:贫富之间的 深层差距及其规模不变性质。特别是,在我们的模拟中,只有
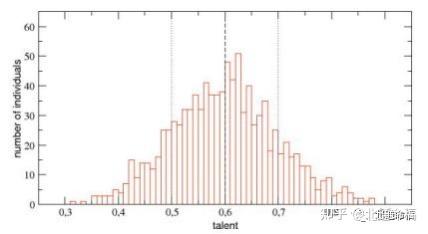
图2 . 人才在人口中的正态分布(平均数为mT= 0 . 6,用虚线表示,标准差为aT= 0 . 1_其中的值mT干 a T用
两条垂直的虚线表示)。这个分布在区间½0;1]中被截断,并且在模拟过程中不会发生变化。
(b)
图3 . 资本/成功在人口中的最终分布,包括在(a)对数-林和(b)对数-对数尺度上。尽管人才呈正态分布,但 成功分布的尾部可以在面板(b)中看到,可以用斜率为1的幂律曲线很好地绘制出来。2 7 . 我们还证实,资本/ 成功分配遵循帕累托的\80-20“规则,因为20%的人口拥有80%的总资本,而剩下的80%拥有20%的资本。
4个个人拥有超过500个单位的资本,20个最成功的个人持有资本总量的44%,而近一半 的人口保持在10个单位以下。在全球范围内,帕累托的\80-20“规则得到了尊重,因 为80%的人口只拥有总资本的20%,而剩下的20%的人拥有同一资本的80%。虽然这种差 距看起来肯定不公平,但如果最成功的人是最有才华的人,这在某种程度上是可以接 受的,所以值得积累更多的资本/成功。但事情真的是这样的吗?
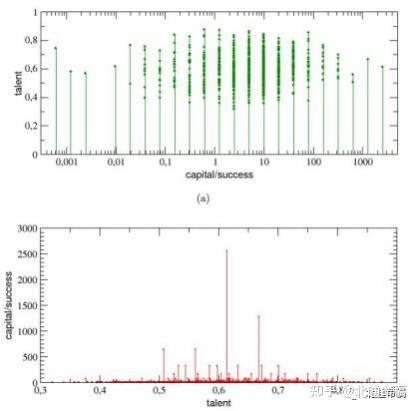
图(a)和(b)。4,人才分别被绘制成¯的资本/成功的函数,反之亦然 (注意,在面 板(a)中,资本/成功只取不连续的值:这是由于选择对所有代理使用一个相等的整数 初始资本) 。看这两个面板,很明显,在其中一个
(b)
图4 . 在面板(a)中,人才被绘制成资本/成功的函数 (以对数尺度来更好地可视化) :很明显,最成功的人并 不是最有才华的人。在面板(b)中,反之亦然,资本/成功被绘制为人才的函数:在这里,我们可以进一步认 识到,最成功的代理,与Cmax= 2560,其天赋仅略大于平均值mT= 0 . 最有才华的公司的资本/成功低于C = 1 ,初始资本Cð0Þ要少得多。详情请参见文本。
手中,最成功的人并不是最有才华的,另一方面,最有才华的人也不是最成功的。特 别是最成功的人,有Cmax= 2560,有一个很有天赋的T*= 0. 61,仅略大于平均值mT= 0 . 而最有才华的一个(Tmax= 0.89)的资本/成功率低于1个单位(C = 0。625).
正如我们将在下一节的小节中看到更多的细节,这样的结果不是一个特殊的情况, 而是这种系统的规则:最大的成功永远不会与最大的人才相一致,反之亦然。此外, 这种成功和人才之间的失调是不成比例的和高度非线性的。事实上,所有有人才的平 均资本是T > T*是C写20:换句话说,最成功的人的资本/成功是128
比比他更有才华的人的平均资本/成功程度高几倍。我们可以得出这样的结论,如果一 些人的巨大成功背后没有非凡的才能,另一个因素可能在起作用。我们的模拟清楚地 表明,这样一个因素纯粹是运气。
在无花果。据报道,所有人在工作生涯中发生的幸运和不幸事件的数量是他们的资 本/成功的函数。从(a)小组来看,很明显,最成功的人也是最幸运的人 (注意,在这 个小组中报告了所有发生在特工身上的幸运事件,而不仅仅是那些他们利用的事件, 与他们的天赋成比例) 。相反,看面板(b),结果是不太成功的人也是最不幸的人。换 句话说,虽然成功和模拟产生的天赋之间没有相关性,但也有一个非常强的关联
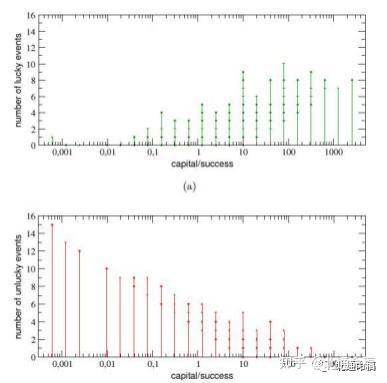
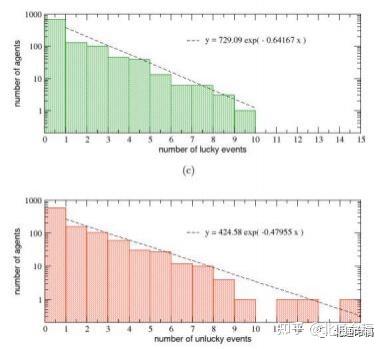
. (a)幸运事件或(b)不幸事件的总数作为代理的资本/成功的函数。故事情节显示了成功和运气之间存在 着很强的相关性:最成功的人也是最幸运的,而不太成功的人也是最不幸的。 同样,在对所有代理使用初始 资本相等的初始资本后,就会有几个事件被分组为资本/成功的不连续值。在面板(c)和(d)中,分别将幸运事 件和不幸事件的数量以对数线性尺度报告的频率分布。 由此可见,这两种分布都可以用负指数相似的指数分 布很好地表示。
(d)
图5 . (续)
成功和运气之间的相关性。通过分析个体中发生的幸运或不幸事件数量的频率分布的 细节,我们发现——如面板(c)和(d)所示——它们都是指数级的,指数为0。64和0。 48,平均1。35和1。分别为66,幸运或不幸事件发生的最大数量分别为10和15。此外 ,大约16%的人有一种\中立的“生活” ,根本没有幸运或不幸的事件,而大约40%的人 只经历了一种类型的事件 (幸运或不幸的事件) 。
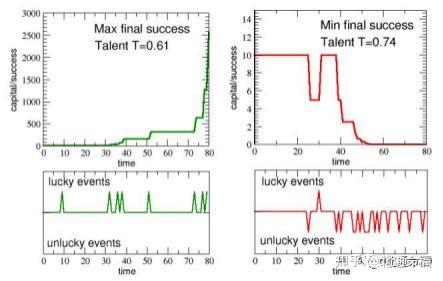
与他们工作生活的40年 (80个时间步,每6个月一次) 中发生的相应的幸运或不幸 事件序列相比,观察最成功和较不成功的人的成功/资本的时间演变也是很有趣的。这 可以分别在图的左边和右边的部分观察到。6 . 从图的面板(a)中就可以看出。在这个¯ 裁判的底部面板中,只有幸运的事件,经纪人利用了他们的天赋。
在第(a)组中,关于中等才华但最成功的人,很明显地表明,在他工作生涯的前半 段幸运事件 (底部) ,然后资本水平低 (顶部) ,
(a)
(b)
图6. (a)最成功的成功/资本的时间演变和不成功的(b),与相应的幸运或不幸事件的序列(80个学期,i。 e.,40年)。这些事件发生的时间在底部的面板中显示,带有向上或向下的峰值。
在30到40个时间步之间的突然集中(i。e., 就在40岁之前)产生了资本的快速增长,在 最后10个时间步中呈指数增长。e., 经纪人职业生涯的最后5年),从C = 320到Cmax=
2560.
另一方面,看 (顶部和底部) 面板(b),关于不太成功的个人,很明显,一个特别 不幸的工作生涯的后半段,与十几个不利事件,逐步减少资本/成功,使它的¯值C = 0 。00 0 6 1 . 有趣的是,这个可怜的经纪人有一个天才T = 0。比最成功的药剂的数量要 大。显然,好运使了成功。,如果它是真的,最成功的代理的优点利用所有的机会提 供给他 (尽管他的平均天赋) ,这也是真的,如果你的生活一样不幸和贫穷的机会的 其他代理,甚至一个伟大的人才变得无用的对不幸的愤怒。
本小节中显示的单个模拟运行的所有结果a非常健壮,正如我们将在下一个小节中 看到的,如果我们重复多次从相同的人才分布开始,但个体的随机位置,它们会有很 小的随机位置。
用于单次运行模拟的TvL模型的NetLogo代码的演示版本可以在开放的ABM存储库_ https:// www 上找到。 http:// comses.net/codebases/ .
2 . 2 . 多次运行结果
在本小节中,我们将展示一个超过100次运行的模拟平均的全局结果,每次运行都从两 个随机初始条件开始。控制参数的值与上一小节中使用的值相同: N = 1000个体, mT= 0 . 6和aT= 0 . 1对于正态人才分布,I = 80迭代(每个迭代代表6t=6个月的工作寿 命),Cð0Þ= 10个初始资本单位,NE=的500个事件点数和一个百分比pL= 50%的幸运事 件。
在图的面板(a)中。7、在100次运行中收集到的所有代理的¯年资本/成功的全球分 布以对数-对数尺度表示,并由斜率为_1的幂律曲线表示。3 3 . 资本的尺度不变行为 和随之而来的个人之间的强烈的不平等,以及帕累托的\80-20“(b)
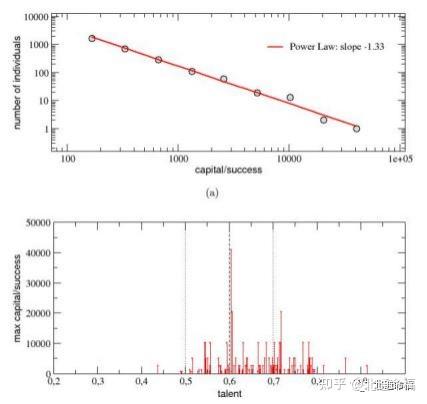
图7. (a)对具有不同随机初始条件的种群计算超过100次运行的¯自然资本/成功分布。该分布可以用斜率为_1 的幂律曲线很好地表示。3 3 . (b)自然资本Cmax在100次比赛中最成功的人被认为是他们天赋的功能。平均而 言, 中等高天赋的人比中低天赋的人更成功,但最成功的人往往是中等天赋的经纪人,很少是最有天赋的人 。他们T值,连同值m一起T干 a T,也分别报告为垂直虚线和点线。
因此,在单次运行模拟中观察到的规则,在多次运行的情况下也是保守的。事实上, 富人(成功) 和贫穷(不成功) 代理人之间的差距已经扩大,因为最成功的人的资本
现在超过了40,000个单位。
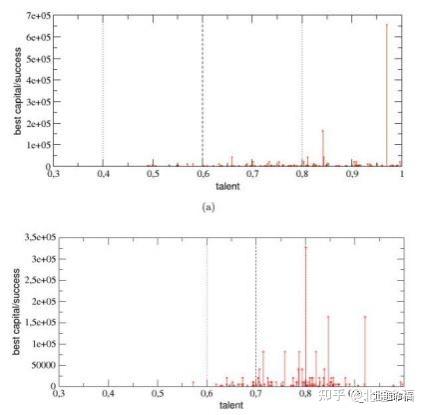
最后一个结果可以更好地欣赏面板(b),其中自然资本Cmax在最成功的人中,我。 e., 100次跑步中每一次的最佳表现,是他们天赋的功能。最好的分数是由一个有天赋 的经纪人来实现的最好的= 0 . 6048,实际上与人才分配的平均值相一致(mT= 0. 6), 他达到了资本C的顶峰最好的= 4 0 ; 9 6 0 . 另一方面,在最成功的人中最有才华的人 ,有人才Tmax= 0.91、累计资本Cmax= 2560 ,仅等于C的6%最好的.
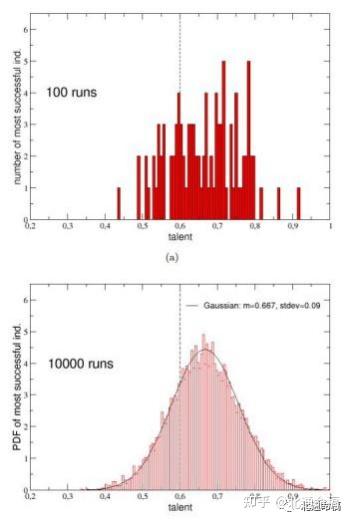
为了更详细地解决这一点,在图中。8(a),我们绘制了计算超过100次。该分布似 乎转向了人才轴的右侧,其平均值为Tav= 0.66 > mT:一方面,中高人才往往是取 得巨大成功的必要条件;但是,另一方面,它也表明它几乎从来没有天赋,因为代理 拥有最高的人才(e。g., 与T > mTþ 2aT, i.e., 与T > 0。8)的结果只有在3%的情 况下表现最好,他们的资本/成功从未超过13%的C最好的.
在无花果。8(b),相同的分布 (归一化到酉区域以获得PDF) 计算超过10;000次运 行,以欣赏它的真实形状:它似乎由平均T的高斯GðTÞ很好地绘制av= 0.标准为667, 标准差为0。09 (实线) 。因此,最佳表演者的人才分配相对于人才的原始分配被转移 到人才轴的右边。更准确地说,这意味着条件概率PðCmaxjTÞ=GðTÞdT和表现最好的人 在间隔½T;TþdT]随着人才T增加,在中高人才T附近达到最大值av= 0. 66、然后迅速 下降,人才价值越高。换句话说,¯和一个适度有天赋的人获得成功的概率高于¯和一 个非常有天赋的人获得的概率。请注意,在一个以人才是成功的主要原因的理想世界 里,人们期待着PðCmaxjTÞ是T的一个递增函数。因此,我们可以得出结论,所观察到 的PðC的高斯形状maxJTÞ证明,运气比人才更重要。
比较平均资本/成功的C也很有趣mt) 63次,超过100次跑步,最有才华的人才和相应 的平均资本/成功C在) 33个有天赋的人非常接近平均的mT.我们发现在这两种情况下都有
相当小的值 (尽管大于初始资本Cð0Þ= 10) ,但事实是Cmt> C在表明, 即使¯和一个
中等有天赋的人在成功的概率高于¯和一个非常有才华的人,最有才华的人,平均而言, 比中等有天赋的人有更多的成功。另一方面,看看平均百分比,超过100次跑,是
(b)
图8 . (a)人才分布的最成功的个人 (最好的表演者) 在每一个100次运行。(b)最成功个体的人才概率分布函数 计算超过10;000次运行:采用平均0:667和标准差0:09的正态分布 (实线) 。平均mT¼0:6的人口中人才的 原始正态分布被报告为两个面板中的垂直虚线进行比较。
有天赋的人T > 0:7 (i。e., 大于与平均值的一个标准差)和总体成功/资本¯最后部 分> 10,计算对所有的代理人才T>0:7 (平均每次运行,、160) ,我们发现这个比例 等于32%:这意味着最优秀的人才的总性能在我们的人口仍然,平均而言,相对较小, 因为只有三分之一达到¯资本大于初始。
在任何情况下,在100次模拟运行中绝对表现最好的是一个有天赋T的代理最好的= 0 . 6、与平均值完全一致,但最终成功了¯最好的= 40;960,是C的650倍mt比成功C的 4000多倍最后部分< 10的2/3的最有才华的人。这只是因为,在故事的结尾,她只是比 其他人更幸运。的确,非常幸运,如图所示。在她的工作生涯中,她的资本/成功的增 加,以及一连串令人印象深刻的幸运 (也是唯一的幸运) 事件,尽管她缺乏特殊的天 赋,但她能够在她的职业生涯中利用这些事件。
总结,已经发现现在,尽管其简单,TvL模型似乎能够占许多特性特征,讨论的介 绍,不平等的很大程度上的分布在我们的社会,在明显与人类人才的高斯分布。与此 同时,该模型在数量上表明,一个伟大的人才并不能保证一个成功的职业生涯,相反 ,没有天赋的人往往能够达到成功的顶峰——另一个程式化的事实“经常观察到的现 实生活[34,35,37]”。
直觉地解释了中等天赋的人 (经常) 比更有天赋的人获得更大的荣誉和成功的关键 是运气的隐藏的和经常被低估的作用
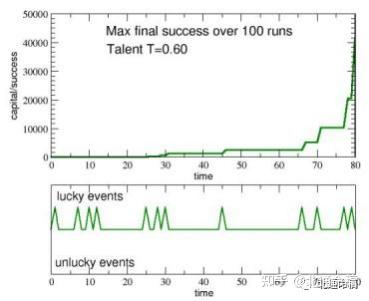
图9 . 在100次模拟运行中,最成功 (但具有中等天赋) 的个体的成功/资本的时间演变,与她在工作生活中发 生的相应的不寻常的幸运事件序列相比。
我们的模拟。但要理解我们的¯信息的真正意义,区分宏观和微观的观点是很重要的。
事实上,从微观的角度来看,遵循TvL模型的动态规则,一个有天赋的人比一个中 等天赋的人有更高的先验概率,因为她有更大的能力抓住任何机会。当然,运气必须 帮助她创造这些机会。因此,从一个人的角度来看,我们应该得出这样的结论:不可 能 (通过¯) 控制幸运事件的发生,最好的策略增加成功的概率 (在任何人才水平) 是 扩大个人活动,思想的生产,与他人的沟通,寻求多样性和相互浓缩。换句话说,成 为一个思想开放的人,准备好与他人接触,暴露在最高的可能性下的幸运事件 (通过 个人才能被利用) 。
另一方面,从宏观的角度来看,整个社会的概率和适度有天赋的个人顶层的成功大 于¯天才,因为适度有天赋的人更多,运气的帮助下,在全球统计优势达到一个巨大的 成功,尽管他们的低个人先验概率。
在下一节中,我们将解决这样一个宏观角度探索的可能性由我们的模型详细调查新 的和更多的策略和政策提高最有才华的人的平均性能,实现更多的方式分配奖品和资 源。事实上,作为最有才华的人,作为我们社会进步和创新的引擎,我们希望任何政 策都能提高他们的水平
成功的人将会对集体生活产生有益的影响。
3 . ®.平衡运气的有效策略
前一节给出的结果与在介绍中讨论的大量实证证据非常一致,¯严肃地质疑天真的精英 假设,即在天赋、技能、能力、智力、努力工作或决心方面的自然差异是成功的唯一 原因。正如我们所展示的,运气也很重要,它可以发挥非常重要的作用。解释的观点 是,作为需要衡量的个人品质 (在许多情况下几乎没有严格规定) ,用来分配荣誉、 资金或奖励的精英策略通常往往基于个人表现,即个人财富或成功。最终,这些策略
发挥进一步的强化作用,通过正反馈机制增加最幸运的人的财富/成功,这类似于著名
的\富人变富”过程(也称为\马修等”[56 – 58]),具有不公平的¯全国性结果。 例如,让我们考虑一个公共资助的研究授予委员会使用¯的资金。为了增加对平均水平的 影响研究,是给一些明显优秀的研究人员提供更大的资助,还是给更多明显普通的研究人 员提供小额的资助?[43]最近的一项研究,基于对涉及出版物的四种科学¯影响指标的 分析,发现影响与资金方面是积极的,但只是微弱的相关。特别是,每一美元的影响 对大型资助持有人来说,要较低,而获得资金增加的研究人员的影响并没有明显增加 。该研究的作者得出结论,科学¯的影响 (由出版物引用) 只受到资金的微弱限制,并 表明针对不同的想法,而不是卓越的资助策略,可能更有成效。最近的贡献[59]表明 ,在论文的数量和他们的科学¯的影响,研究资金的集中通常产生边际收益递减,而且 最资助研究人员不突出的输出和科学¯的影响。实际上,这样的结论不应该令人惊讶, 因为最近的其他¯新[17],影响,正如在基本出版物中衡量的,是随机分布在一个科学 家的时间序列内发表的出版物。换句话说,如果运气很重要,如果它比我们愿意承认 的更重要,那么精英主义策略显示出比预期更少的效果并不奇怪,特别是,如果我们 试图在事后评估价值。在之前的研究中 – ,已经有了对这种天真的精英统治的警告” ,显示了基于管理、政治和¯方面的随机选择的替代策略的可行性。与这样的观点一致 ,TvL模型显示了如何达到最大的最低成功水平
在一个运气很重要的世界里,有才能的人才可以增加往往是重要发现的原因。
3 . 1 . 意外、创新和融资策略
“\意外发现”一词在文献中通常用来指历史证据,即研究人员在寻找其他[60,61]的 时候,经常偶然做出意外的和有益的发现。有一长串幸运的发现:从亚历山大 ·弗莱 明的青霉素到玛丽 ·居里的放射性,从射电天文学家阿诺 ·彭齐亚斯和罗伯特 ·伍德 罗 ·威尔逊的宇宙微波背景辐射,到安德烈 ·盖姆和科斯蒂亚 ·诺沃塞洛夫的石墨烯 。最近的一个例子, ° °-¯通道网络在人体,这可能是一个未知的器官,似乎有助于 运输癌细胞周围,偶然发现,从常规内窥镜[62]。因此,许多人认为,好奇心驱动的 研究应该一直得到资助,因为没有人能真正知道或预测它可以在哪里导致[63]。
有可能量化意外发现的作用吗?哪些是最容易刺激意外发现的方法?偶然发现可以 有多种形式,限制和量化是双重崇拜。这就是为什么,到目前为止,学术研究主要集 中在科学中的意外发现作为一种哲学思想。但事情正在改变。
欧洲研究理事会最近给了生化学家Yaqub a 1。700万美元的拨款,用于量化意外发现 在科学[64]中的作用。Yaqub发现,将意外发现可以分为四种基本类型[65],并且可能 存在影响其发生的重要因素。他的结论似乎与早期作品[66 –71]中提出的观点一致, 这些观点认为普遍采用的——显然是精英策略——追求卓越和驱逐多样性,似乎注定 是失败和失败的。原因是,他们剔除了最初看起来不那么希望的先验研究,但也多亏 了意外发现,可能是非常创新的后验。
从这个角度来看,我们希望使用TvL模型,它自然地将运气 (因此也包括意外发现 ) 作为政策的定量工具,以便在本小节中,探索不同融资场景的有效性。特别是在上 下文中,如上讨论,平均天才但幸运的人往往比更成功天才但不幸的人,重要的是评 估±的环境融资策略保持最低水平的成功也对最有才华的人,有望产生最进步和创新 的想法。
从Sec中使用的相同参数设置开始。2.2, i. e., N ¼ 1000, mT¼ 0.6, aT¼ 0.1, I ¼ 80, 6t¼ 6, Cð0Þ ¼ 10, NE¼ 500, pL¼50%和100模拟运行,让我们想象一 个给定的总资金资本FT根据不同的标准,定期在个体之间分布。例如,资金可以分配 如下:
(1)在同等程度上 (平等主义标准) ,以促进研究的多样性;
(2)只针对一定比例的最成功的 (最好的”) 个人 (精英主义标准) ,这在以前被天真 地称为“精英主义” ,因为它根据人们过去的表现向他们分配资金;
(3)通过将保费分配给特定比例的最成功的个人,而剩余金额的比例则等于所有其他个 人 (混合标准) ;
(4)只对给定百分比的个体,随机选择 (选择性随机标准) ;
我们实际地假设总资本FT将每5年分发一次,在每次模拟运行期间的40年里,例如 fT/8单位将不时分配。由于这些资金的定期注入,我们打算为最有才华的代理商保持 最低水平的资源。因此,对于所采用的筹资战略的有效性,一个很好的指标可以是®的 百分比T,平均超过100次模拟运行,有天赋的人Tþ aT其的成功/资本大于最初的,¯ 。e.C最后部分> Cð0Þ .
这个百分比已经被计算出来了,在第二秒中提出的多次运行模拟中。2 . 2 . 在那里 ,我们已经证明,在没有资金的情况下,这是最好的
表现是由非常幸运的经纪人,他们的天赋接近平均水平,而最有才华的人的资本/成功 总是很低。特别是,只有一个百分比PT0在模拟结束时,T>为0:7的代理总数的32%达 到了资本/成功大于初始资本/成功。因此,为了比较不同融资策略的有效性,平均百 分比±T在他们的职业生涯中,增加了他们的初始资本/成功的人才,应该根据P来计算 T0.让我们把这个增量为¯T*¼ P T— P T0.后一个量是一个非常稳健的指标:我们已经 检查了重复100次模拟集,P值的变化T*仍低于2%。最后,如果我们考虑了PT*和总资本FT 在40年的所有代理商中,可以得到一个风险指数¯ ,即每单位投资资本中优秀成功人才 的增加,即¼¯/¯T*T.
如图表所示。10,我们报告了几种资金分配策略的风险风险指数 (第二列) ,每一 种策略都有不同的资金目标 (第一列) ,以及相应的±值T (第三列) 和PT* (第4列) 。总资本FT每次运行的投资也在最后一列中报告。e环境指数±已归一化为其最大值 ±max和各种记录 (行) 已经被排序的递减值

图1 0 . 资金策略表。标准化环境指数±的结果范数从上到下按递减顺序报告 (第二列) ,对于几种具有不同 目标的资金分配策略 (第一列) 。对应的百分比PT成功的人才及其净增长的PT*关于“\没有资金”的案例,平 均在100次模拟运行中,也分别报告在第三列和第四列。最后,总资本FT在每次运行中进行的投资可以在最后 一列中看到。
E范数= E/Emax.对于无资助案例, 由¯范数= 0.E的分数相同范数也在图中以直方图 的形式进行了报道。11、作为所通过的筹资战略的一个功能。这是多亏了P的统计稳健 性T,显示波动小于2%,报告的环境指数±范数特别稳定。
看表格和图中的相对直方图。11日很明显,如果目标是奖励最有才华的人 (从而增 加¯水平的成功) ,更方便的定期分配 (甚至小) 等量的资本所有个人而不是给更大的 资本只有一小部分,选择通过他们的成功水平_manrat_此刻的分布。
一方面,直方图显示,每5年向所有个人分配1个单位资本的“\平等主义”标准是 最有效的资金分配方式范数= 1 ( i . e ., E = Emax):与一个投资相对较小的FT在 8000个单位中,成功的优秀人才的比例可以增加一倍T0=32:05%至PT= 69:48%,净 增长PT* = 37 :43%.考虑到总投资资本的增加 (例如,将平等主义配额设置为2或5个单 位) ,这一策略还确保了成功人才的百分比的进一步增加

图1 1 . 几种融资策略的标准化e±风险指数。标准化的环境指数±的值范数被报道为当前融资策略的功能。¯ 方法表明,为了增加更多有才华的人才与C最后部分>Cð0Þ认为,它更应该向许多个人提供少量资金,而不是 以其他更有选择性的方式提供资金。
人PT(从69年。48%到84 。02%至94。40%),即使标准化的e环境从±逐渐减少范数=1到 E范数= 0.74和到E范数= 0.37.
另一方面,精英主义的“策略是每5年将资金 (5、10、15、15或20个单位) 分配给 最好的50%、25%甚至10%已经成功的个人都在排名中垫底,E范数< 0. 25: 在所有这些 情况下,净增加了PT*在成功的人才中,没有资金的情况仍然非常小 (在几乎所有的情 况下都小于20%) ,如果与平等主义战略相比,通常反对更大的投资资本。这些结果确 实强化了这种方法只是明显的_i的论点。e., 天真无邪的精英。
值得注意的是,采用一个\混合的“标准,i。e., 将精英主义的“资金份额分配给 一定比例的最成功的个人,例如25%,并将剩余资金同等地分配给其他人,与天真的精 英主义”方法相比,风险指数值得到更好的分数。然而,这一策略的性能并不能超过 “\平等主义”的标准。例如,从资金表的第六行和第四行之间的比较中可以明显看出 ,尽管总投资为16;000单位,但P的价值T用混合准则得到的结果远低于用平等主义方 法得到的标准(70。83%对84。02%),也符合对应的±指数¯的值范数 (0.55对0.74) 。
如果考虑心理因素 (在本研究中没有建模) ,混合策略可以根据平等主义策略重新 估值。事实上,溢价奖励_分配给更成功的个人_可以诱导所有代理走向更大的承诺, 而平均分配的部分将发挥双重作用:在个人层面上,它将在培养多样性和为不幸的人 才提供新的机会来表达他们的潜力,而喂养意外发现在总水平,从而导致研究和整个 社会的进步。
再看一遍融资策略表,也值得强调随机策略惊人的高优势,它在一般排名中占据了 三个最佳分数中的两个。例如,结果表明,只对随机选择的10%的个体给予5个单位的 定期奖励,总投资只有4000个单位,净增加PT* = 17;78%,大于几乎所有用主义策略获 得的结果。此外,将随机资助人员的比例增加到25%,并使总投资加倍 (使其达到 10,000个单位) ,净增加PT* = 35.95%与最佳平等主义策略的¯相当,在±排名第一。 值得注意的是,后者对PT*大约是这个值的四倍(PT* = 9 . 03%)采用精灵主义方法 (见表 中第12行) ,将完全相同的资本 (10,000个单位) 分配给完全相同数量的个人 (占总 数的25%) 。后者是一个进一步的证明,在复杂的社会和经济环境中,机会起着相关的 作用
±基于随机选择的替代策略的适应性很容易超过基于“天真的精英主义”方法的标准 策略。这种违反直觉的现象,已经在管理、政治和¯金融中观察到[47] – 54],¯因此在 研究资助的背景下也有新的证据。
为了进一步证实这些结论,见图。12、给出了另一组模拟的结果。与之前的模拟不 同的是,在100次运行中的每一次运行中投资的总资本现在都被削减为¯T=为 80 ;00 0 , 所 以 那 个FT/8 = 10;每5年向代理商分配000个单位。看看表格,平等主义战略的 结果再次最有利于回报最有才华的人,以一个百分比PT接近100%,紧接着是随机策略 (50%的随机资助的个人) 和混合策略,一半的资本分配给25%的最成功的个人,另一 半同样分配给剩余的人。相反,所有的精英主义策略都被放在排名的底部,从而进一 步形成了天真地精英主义的奖励真正人才的方法。
本小节中提出的TvL模型模拟的结果关注了外部因素 (事实上,如相关的资金政策 ) 在增加最有才华的个人的成功机会方面的重要性,这些人往往受到不幸事件的惩罚 。在下一节的小节中,我们将调查新的机会在多大程度上可以由环境的变化产生,例 如人们生活或来自的社会环境所接受的教育水平或受到的其他刺激。
. 2 . 3.环境对环境的重要性
首先,让我们估计一下平均教育水平在人口中的作用。在TvL模型中,后者可以通过改 变人才的正态分布参数来得到。实际上,假设个人的人才和技能,如果受到刺激,可 以更有利于利用新的机会,
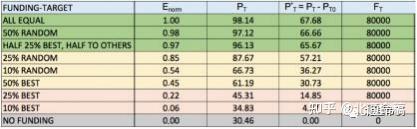
图1 2 . 资金策略表与¯的基金。标准化环境指数±的结果范数对几种具有不同目标的资金分配策略,从上到下 再次按递减顺序报告 (第一列) 。与图的方差。现在每次投资的总资本被¯削减为FT= 8 0 ; 0 0 0 . 平等主义 的策略再次处于排名的首位。
平均m的增加T或者是标准差aT人才分配可以解释为政策的目标,即提高平均教育水平
或加强对最有天赋人才的培训。
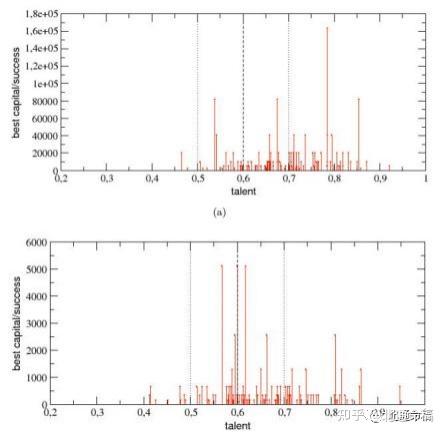
在图的两个面板中。13、我们报告了在100次比赛中表现最好的人积累的¯资本/成 功,作为他们天赋的功能。参数设置与Sec中的相同。2.2 (N = 1000, I = 80, 6t= 6, Cð0Þ = 10, NE= 500和pL= 50%),但没有人才分配的时刻。特别是,在面 板(a)中,我们保持m不变T=值为0:6,但增加了aT= 0:2,而在面板(b)中,我们做了 相反的事情,留下了aT=值为0:1,但增加了mT= 0 : 7 . 在这两种情况下,最大成功高 峰的右侧移动可以欣赏,但有不同的细节。
(b)
图13 . 在100次跑步中,最成功个体的¯资本是他们的人才分布参数的人口: (a) mT= 0:6和aT=0:2 (这代 表了对最有天赋的人的训练强化) ; (b) mT= 0:7和aT=0:1 (代表平均教育水平的提高) 。对应的mT和mT干 a T这些值也分别用垂直的虚线和点线表示。
实际上,它会导致增加aT不改变mT,如面板(a)所示,增加了更多有才华的人获得 非常高的成功的机会:最好的表演者,现在,是一个非常有才华的经纪人与T = 0:97 ,他达到了一个令人难以置信的资本/成功水平C最好的= 655 ; 360.这一方面可以被 认为是积极的,但另一方面,这是一个孤立的情况,作为一个对应的情况,它增加了 不成功人士和成功人士之间的差距。
现在看面板(b),结果是增加mT不改变T制作表现最好,用C最好的= 327;680和一 个天才T = 0:8,然后是另外两个与C = 163;840和,分别是T = 0:85和T = 0:92 。这意味着在这种情况下,更有才华的人获得非常高成功的机会增加了,而不成功和 成功的人之间的差距比以前更小。
最后,在这两个考虑的例子中,超过100次跑步的大多数人才的资本/成功的平均值 相对于C值有所增加mt写63。2.2 .特别是,我们发现了Cmt面板(a)和C的写319mt写 122,但这些值对模拟运行的规格集相当敏感。为了量化这里所调查的社会政策的有效 性,一个更可靠的参数再次是指标PT在上一节中介绍的是,i。e .,人才的平均百分 比Tþ a T和市场成功/资本¯最后部分> 10,超过拥有人才的个人总数Tþ a T(请注意 ,现在,在所考虑的这两种情况下,mTþ aT= 0 :8) .特别是,我们发现了PT面板(a) 和P的=值为38%T=37:面板(b)为5%,相对于参考值P略有净增加T0=为32%(获得的人才 分配与mT= 0:6和aT= 0 :1) .
总结,我们的研究结果表明,加强培训最有天赋的人或增加平均教育水平,可以预 期,一些有益的社会系统,因为这两种政策提高概率,有才华的人,抓住运气给他们 的机会。另一方面,增强的平均百分比的人才能够达到良好的成功水平似乎不是特别 显著的情况下分析,因此相应的教育政策的结果似乎主要局限于孤立的极端成功的情 况下。
当然,一旦一个特定的教育水平被¯了,很明显,大量的机会被社会环境,® 。e., 在人们意外出生或选择居住的国家,这是影响该系统全球性能的另一个关键因素。
在无花果。14,我们展示了与之前¯gure中显示的结果,但对于另一组模拟,每个 运行100次,与Sec相同的参数设置。2.2 (N = 1000, mT= 0 :6, aT= 0 :1, I = 80, Cð0Þ = 10, NE= 500)和第二个误差百分比®L幸运事件(我们提醒大家,在Sec 。2.2,这个百分比被设置为pL= 50%) . 在面板(a)中,我们设置了pL= 80%,为了模 拟一个非常
(b)
图14 . 据报道,在100次试验中,最成功个体的¯的资本是他们对生活在不同环境中的人口的天赋的作用L幸运 事件的发生: (a) pL= 80% ; (b) pL= 20%.m的值T= 0.6和mT士 aT,带有T= 0. 1也分别用垂直的虚线和 点线表示。
刺激环境,丰富的机会,就像富裕国家和工业化国家,如美国的[25]。另一方面,在 面板(b)中,值pL= 20%重现了一个不那么刺激的环境,机会很少,比如第三世界国家
。
在两个面板中都可以看出,最成功个体的¯成功/资本作为其才能的作用在很大程度 上依赖于pL.
当pL= 80%,如在面板(a)中,与案例p相比,一些具有中高人才的代理能够达到更 高水平的成功L=值为50%,峰值为C最好的= 16 3 ; 84 0 . 另一方面,对于最有才华的 个人来说,资本/成功的平均值,Cmt写149,相当高,更重要的是,指标P也是如此T= 6 2 . 18%(相对于参考文献而言,大约是两次
值PT0= 32%),这意味着,正如预期的那样,有才华的人可以享受到更高比例的幸运事 件。
用®得到了完全不同的结果L= 2 0 % . 事实上,正如在面板(b)中看到的,如果与Sec 的模拟中发现的相比,总体的总体水平非常低。2.2,其峰值值为C最好的只有5120个 单位:这是减少社会不平等的足迹,这是°巩固成功机会的预期结果。根据这些结果 ,还有PT指标达到最小值,平均百分比仅为8。75%的人才能够提高他们最初的成功水 平。
总之,在这节中,我们已经表明,一个刺激的环境,丰富的机会,与一个适当的策 略分配资金和资源,是重要的因素利用最有潜力的人,给他们更多的成功的机会对适 度的天赋,但幸运的是。在宏观层面上,任何能够影响这些因素并维持人才生活的政 策,都将有确保集体进步和创新的结果。
4 . 结论性评论
在本文中,我们从一些非常简单和合理的假设出发,提出了一个基于代理的模型,该 模型能够量化人才和运气在人们职业生涯成功中的作用。模拟结果表明,尽管人才在 代理人之间具有高斯分布,但40年工作寿命后的成功/资本分布遵循幂律,尊重现实世 界中财富分配的80-20“帕累托定律。模拟的一个重要结果是,最成功的经纪人几乎从 来都不是最有天赋的,而是高斯人才分布的平均值——这是文献中经常报道的另一个 程式化事实。该模型显示了幸运事件在决定个体成功的¯水平方面的重要性,但经常被 低估。 由于奖励和资源通常是给那些已经达到高水平成功的人,错误地被认为是能力/ 才能的衡量,这个结果甚至是更有害的抑制,导致最有才华的人缺乏机会。我们的研 究结果突出了我们称之为“幼稚精英统治”的范式的风险,它没有给最有能力的人以 荣誉和奖励,因为它低估了随机性在成功的决定因素中的作用。在这方面,几个不同 的场景被调查为了讨论更多的策略,能够平衡运气的不可预测的作用,给更多的机会 和资源最有才华的—— 目的应该是真正的精英方法的主要目标。这些策略也被证明是 对整个社会最有利的,因为它们倾向于增加研究中的思想和观点的多样性,从而也促进了创新。
我们要感谢Robert H。弗兰克、帕维尔 ·索布科维奇和康斯坦丁诺 ·萨利斯进行了富有成效的讨论和评论。

