小白学统计|面板数据分析与Stata应用笔记（二）

面板数据分析与Stata应用笔记整理自慕课上浙江大学方红生教授的面板数据分析与Stata应用课程，笔记中部分图片来自课程截图。

笔记内容还参考了陈强教授的《高级计量经济学及Stata应用（第二版）》

短面板数据分析的基本程序

1、模型设定与数据

2、描述性统计与作图

3、模型选择

4、报告计量结果

#以啤酒税将降低交通死亡率的假说为例，数据来自陈强教授的《高级计量经济学及Stata应用（第二版）》中的“traffic.dta”数据集。

第一步 模型设定与数据

为了检验假说，构造一个双向固定效应模型

\begin{gathered} fata{l_{it}} = {\beta _0} + {\beta _1}beerta{x_{it}} + {\beta _2}spircon{s_{it}} + {\beta _3}unrat{e_{it}} + {\beta _4}perinc{k_{it}} \hfill+{\mu _i} + {\gamma _t} + {\varepsilon _{it}} \hfill\end{gathered}

其中，被解释变量 fatal 为交通死亡率，核心解释变量 beertax 为啤酒税；另外三个可观测的控制变量: spircons、unrate、perinck 分别为酒精的消费量、税率和人均个人收入； {\mu _i} 为不可观测的个体效应， {\gamma _t} 为时间效应。

在Stata软件中对数据进行分析，执行如下步骤：

1、导入数据到Stata中

在Stata的“命令窗口”中输入

命令【use"数据集路径\traffic.dta"】将“traffic.dta”数据集导入到Stata中，

例如【use"C:\Users\traffic.dta"】。

将数据导入Stata后，即可在Stata的“变量窗口”中看到“traffic”数据集中的各个变量的名称及其标签。

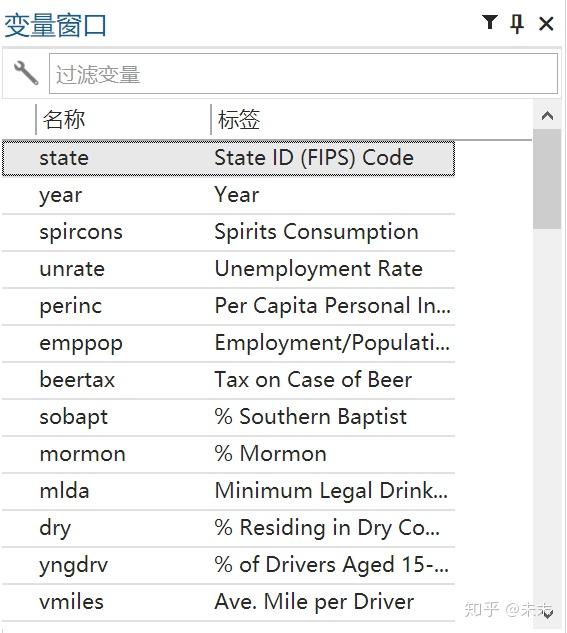
2、查看数据

在Stata的“命令窗口”输入命令【des】查看“traffic”数据集。

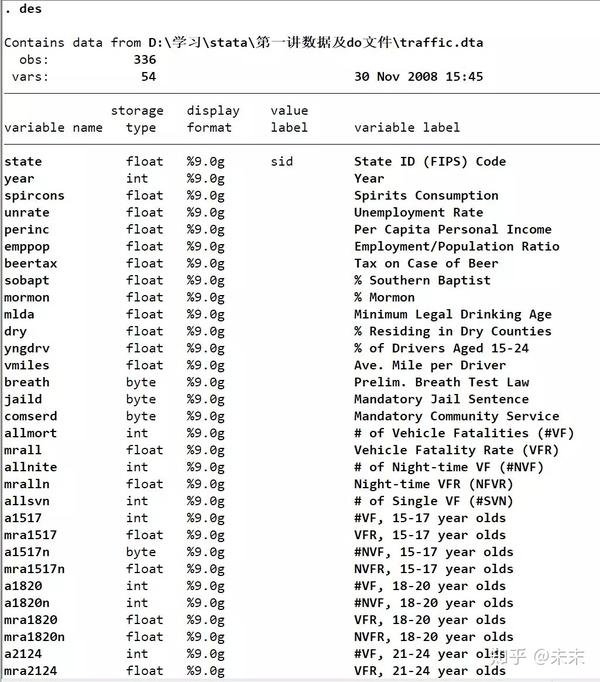
从输出结果我们可以看到：“traffic”数据集包含336个观测值，54个变量。此外，我们还可以看到数据集中的变量名称、数据类型以及相关的说明。
通过命令【xtdes】我们可以查看面板数据的特征。

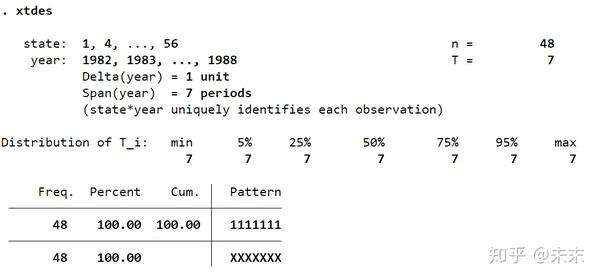
由结果可知：面板数据的截面数 ,时间数 , ,说明这是一个短面板数据集。

在使用面板数据分析前，我们需要输入命令【xtset state year】,来告诉Stata软件，这是一个以截面变量state为州，时间变量为year的面板数据。

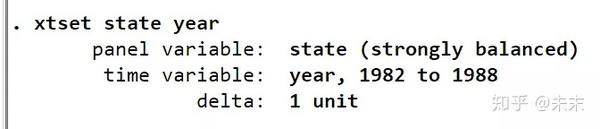
观察输出结果，由strongly balance可知，这是一个平衡面板数据。

至此，我们可以知道，“traffic”数据集是一个48个州，1982-1988年的平衡面板数据集。

第二步 描述性统计作图

1、描述性统计

使用命令【sum 关键变量】可以得到关键变量的描述性统计表。

在Stata中输入命令【sum fatal beertax spircons unrate perinck】,我们可以得到解释变量与被解释变量的观测值、均值、标准差、最小值和最大值。

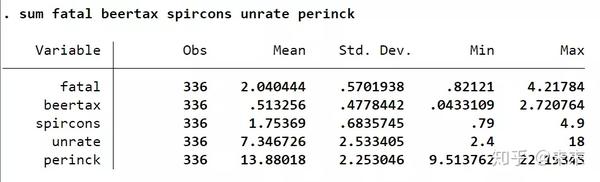
2、绘制散点图及回归直线
在回归之前，我们可以先画出核心变量与别解释变量的散点图及回归直线，来预先判定一下核心变量与被解释变量之间的关系。

使用命令【twoway(scatter fatal beertac)(lfit fatal beertax)】即可画出核心变量“fatal”与被解释变量“beertax”的散点图及回归直线。

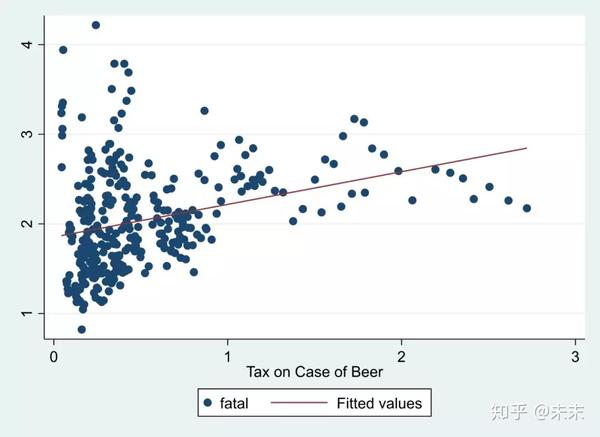
需要注意的是，严格意义上说，这样做并不是正确的，因为并没有控制核心变量之外的其他影响因素。

正确的做法 应该是，在控制其他变量的基础上，展示核心变量与被解释变量的偏相关图。

首先，我们需要使用【reg】命令做出回归结果；

然后，使用命令【avplot 核心变量】即可得到核心变量与被解释变量的偏相关图。

#首次使用avplot的同学，要记得通过命令【search avplot】先安装avplot。

如果直接使用命令【avplots】则会得到所有的变量与被解释变量的偏相关图。

在Stata的“命令窗口”中先输入命令【reg fatal beertax spircons unrate perinck i.year i.state】进行LSDV估计。

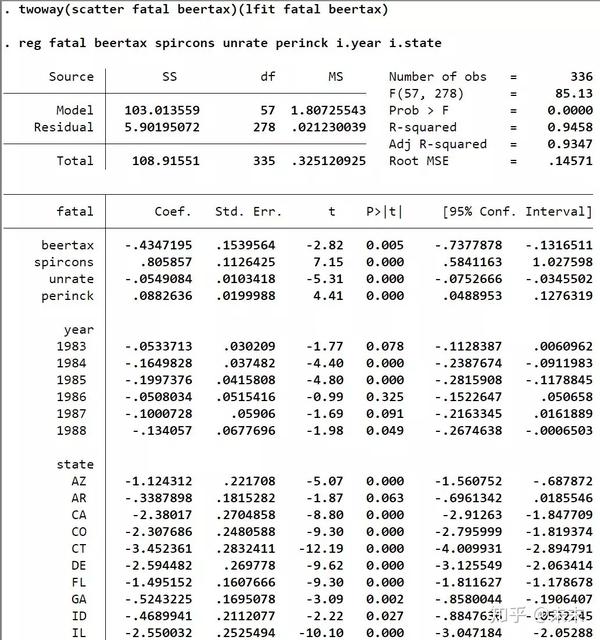
然后，输入命令【avplot beertax】

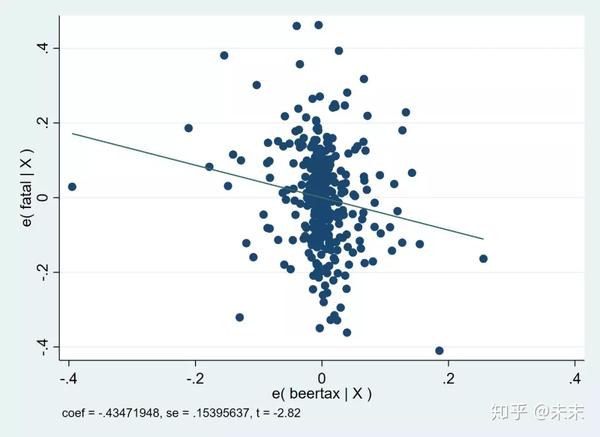
输入命令【avplots】得到所有的变量与被解释变量的偏相关图。

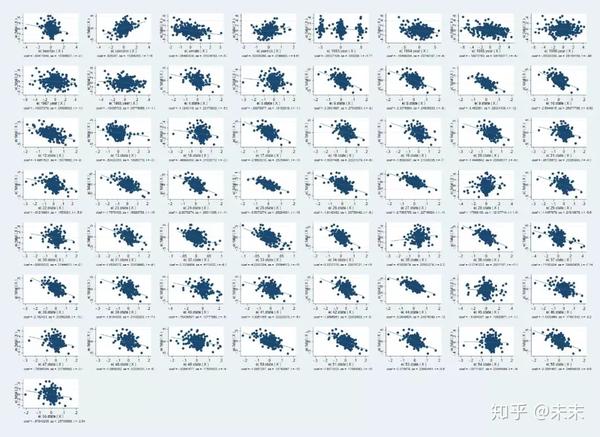
3、绘制核心变量的时间序列图

使用命令【xtline 核心变量】可以做出核心变量在每个截面变量的时间序列图，以研究分析核心变量在每个截面变量中的变动趋势。

在Stata“命令窗口”中输入命令【xtline fatal】即可得到核心变量交通死亡率“fatal”在各个州的时间序列图。

第三步 模型选择

对于固定效应模型、随机效应模型和混合回归模型这三个模型，在实际应用中我们应该选择哪一个模型呢？
一般来说，在学术研究中我们选择双向固定效应模型就可以了。

但是，为了严谨，我们还是应该对三个模型进行比较选择，以判断哪一个模型是匹配数据集的最合适的模型。

1、比较混合回归模型和固定效应模型

首先，我们使用命令【tab year,gen(year)】生成年份虚拟变量；

然后，通过命令【xtreg fatal beertax spircons unrate perinck year2-year7 ,fe】估计双向固定效应模型。

使用命令“xtreg,fe”，在输出结果中我们会得到一个F检验的结果，其原假设为 H_0:all\;{\mu_i=0} 。这意味着，如果接受原假设，就选择混合回归模型；如果拒绝原假设，则选择固定效应模型。

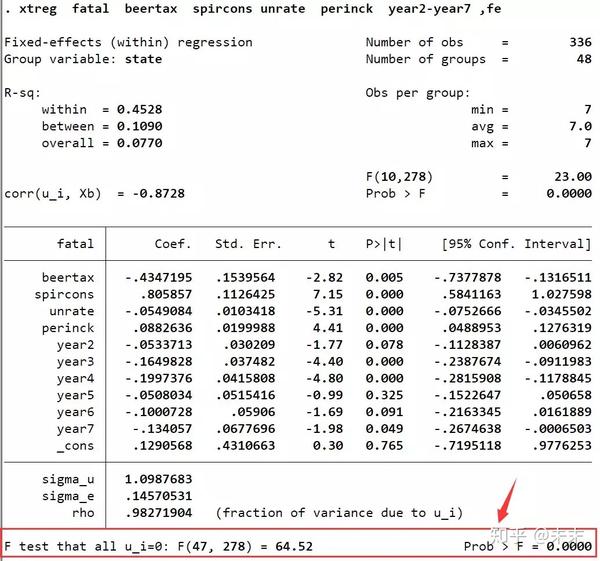
由输出结果可知，F检验对应的P值远小于0.01，那么，这是否就意味着我们可以拒绝原假设，选择固定效应模型呢？

答案是否定的，原因是误差项可能存在自相关、异方差和截面相关这三大问题，如果不对这三大问题进行处理，那么F检验的结果可能就不可靠。

所以，出于严谨性的考虑，我们还需要对这三大问题进行检验。

a.一般来说，先检验截面相关问题

我们可以使用命令【xtcsd】来检验截面相关问题。

#首次使用xtcsdt的同学，需要通过命令【ssc install xtcsd】来安装xtcsd。

“xtcsd”有三个选项，分别为：pes、fri、fre，每个选项都有其使用的前提

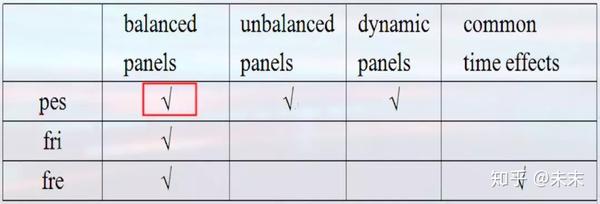
#“xtcsd”命令只可在固定效应模型或随机效应模型估计之后，才可运行

【xtcsd,pes】可以用于平衡面板、非平衡面板以及动态面板；

【xtcsd,fri】只可用于平衡面板；

【xtcsd,fre】可以用于平衡面板，但fre同时考虑了时间效应。

结合案例，我们使用的数据是平衡面板数据，而使用的模型控制了时间效应，所以我们选择命令【xtcsd,fre】

由检验结果可知，因为1.068大于百分之10所对应的临界值0.3583，所以拒绝不存在截面相关的原假设，即认为模型存在截面相关问题。

所以，我们使用之前之前介绍的“xtscc”命令来处理截面相关问题，然后再进行个体效应是否存在的检验。

#首次使用xtscc的同学，需要通过命令【ssc install xtscc】来安装xtscc。

在Stata中输入命令【xi:xtscc fatal beertax spircons unrate perinck year2-year7 i.state】

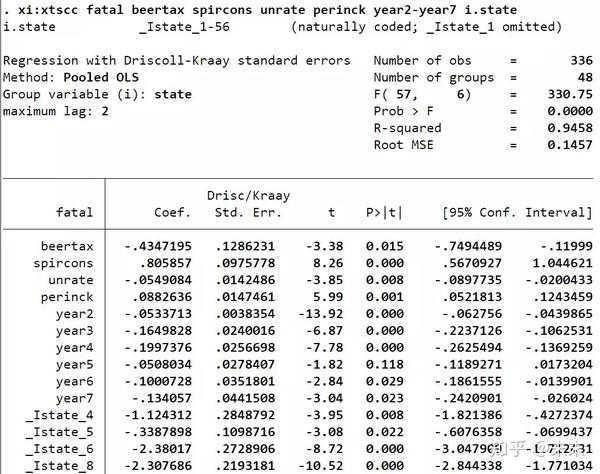
然后，使用命令【testparm _Istate*】对州虚拟变量做F检验

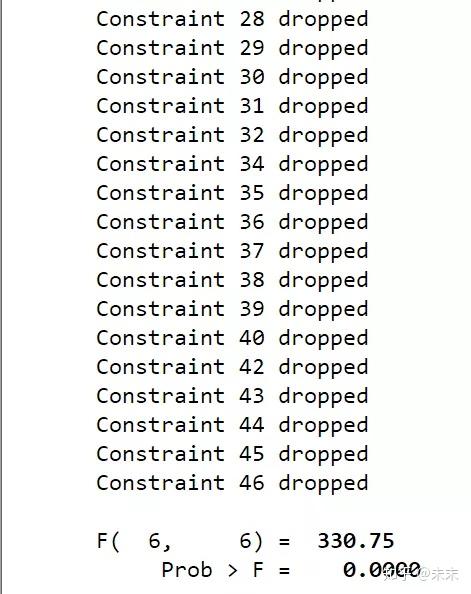
检验结果显示，P值远小于0.1，可以拒绝原假设，认为存在个体效应，所以选择固定效应模型。

b.如果不存在截面相关问题，假定存在异方差和自相关

如果不存在截面相关问题，假定存在异方差和自相关，则使用命令【xi:reg fatal beertax spircons unrate perinck year2-year7 i.state,cluster(state)】

这个命令使用聚类到州获得标准误来处理自相关和异方差问题。

然后，再使用命令【testparm _Istate*】对州虚拟变量进行F检验

2、比较混合回归模型和随机效应模型

Breusch 和Pagan在1980年提出了一个检验个体效应的LM检验。

其原假设为 H_0:\;\sigma_\mu^2=0 ，备择假设为 H_1:\;\sigma_\mu^2\ne0 。

如果拒绝原假设，就选择随机效应模型；如果接受原假设，则选择混合回归模型。

Stata的检验命令为【xttest0】或者【xttest1】

#首次使用xttest0/xttest1的同学，需要通过命令【findit xttest0/findit xttest1】来安装命令。

首先，使用随机效应模型进行估计。在Stata“命令窗口”中输入命令

【xtreg fatal beertax spircons unrate perinck year2-year7,re】

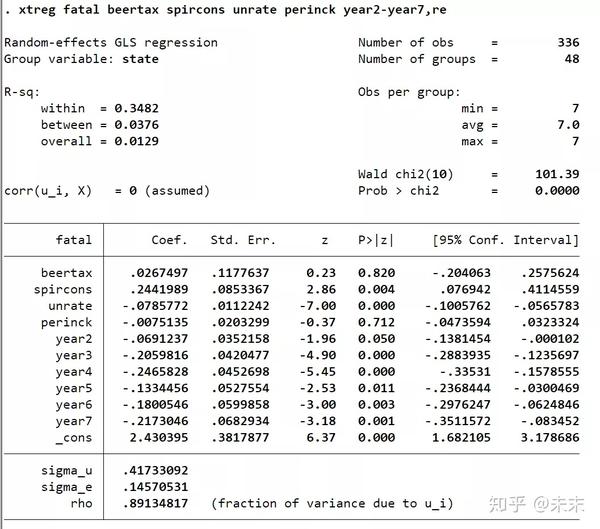
然后，输入命令【xtteat0】

从检验结果，我们可以看到，P值为0，小于显著性水平0.01，所以在0.01的显著性水平下拒绝原假设，选择随机效应模型。

如果误差项存在自相关，使用命令【xttest1】检验随机效应更好。

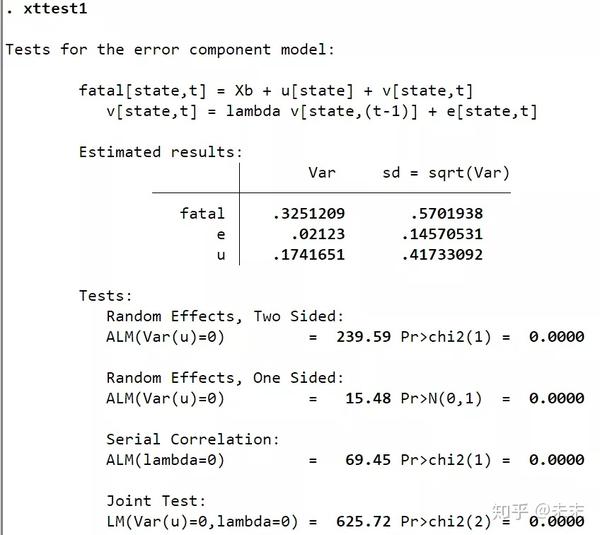
由输出结果可知：Random Effects给出了随机效应自相关的检验结果，由结果可知，随机效应存在一阶自相关问题；Serial Effects给出了误差项的自相关检验结果，检验结果的P值为0，小于0.01，所以在0.01的显著性水平下拒绝原假设，即误差项存在一阶自相关问题；LM检验结果显示应拒绝原假设，即选择随机效应模型。

3、比较固定效应模型和随机效应模型

通常使用Hausman检验进行比较。

Hausman检验的基本思想是：

如果 Cov({\alpha_i},{X_{it}})=0 ，那么固定效应模型和随机效应模型的估计都是一致的，但是随机效应模型更加有效；

如果 Cov({\alpha_i},{X_{it}})\ne0 ，固定效应模型仍然一致，但随机效应模型是有偏的。

所以，如果原假设成立，则固定效应模型与随机效应模型将共同收敛于真实的参数值；反之，两者的差距过大，则倾向于拒绝原假设，选择固定效应模型。

Hausman检验有四行命令（不考虑异方差和截面相关）

称为：Hausman test1

#以“traffic”数据集为例

【xtreg fatal beertax spircons unrate perinck year2-year7,fe】#做固定效应估计

【est store FE】#存储固定效应估计的结果

【xtreg fatal beertax spircons unrate perinck year2-year7,re】#做随机效应估计

【hausman FE, constant sigmamore】/【hausman FE, constant sigmaless】#将两个估计结果进行比较；constant代表masi距离中常数项的估计量；sigmamore利用有效估计量方差，即re；sigmaless利用一致估计量方差，即fe。

由结果可知，检验结果的P值为0，小于0.01，所以在0.01的显著性水平下拒绝原假设，选择固定效应模型。
需要注意的是：Hausman test1并不适合于异方差问题。

解决办法是：构造一个辅助回归。

\begin{gathered} {y_{it}} - \hat \theta \cdot {{\bar y}_i} = ({x_{it}} - \hat \theta \cdot {{\bar x}_i})'\beta + (1 - \hat \theta ){{z'}_i}\delta + ({x_{it}} - {{\bar x}_i})'\gamma + [(1 - \hat \theta ){\mu _i} + ({\varepsilon _{it}} - \hat \theta {{\bar \varepsilon }_i})] \end{gathered}

这个辅助回归是在随机效应模型广义离差变换的基础上，加入一个解释变量的组内离差 ({x_{it}} - {{\bar x}_i}) 。

这个辅助回归的基本思想是：

（1）如果 \gamma=0 ，这和辅助回归方程就等价于随机效应的广义离差变换模型。如果随机效应模型成立，则ols估计是一致的，所以 p\mathop {\lim }\limits_{n \to \infty } \hat \gamma = \gamma = 0 。

（2）如果固定效应模型成立，由于扰动项 [(1 - \hat \theta ){\mu _i} + ({\varepsilon _{it}} - \hat \theta {\bar \varepsilon _i})] 与 ({x_{it}} - {{\bar x}_i}) 相关，所以，ols估计是不一致的，即 p\mathop {\lim }\limits_{n \to \infty } \hat \gamma=\gamma '\ne\gamma = 0 。

#因此，拒绝 H_0:\gamma=0 ,意味着拒绝随机效应接受固定效应。

（3）使用聚类稳健标准误处理异方差问题后，再检验假设 H_0:\gamma=0 。如果拒绝原假设，则选择固定效应；反之，则选择随机效应。

实现程序：Hausman test2

【quietly xtreg fatal beertax spircons unrate perinck year2-year7,re】

#做随机效应估计,"quietly"表示正常执行"xtreg"命令但不输出估计结果

【scalar theta=e(theta)】#得到广义离差中参数 的估计

【global yandxforhausman fatal beertax spircons unrate perinck year2 year3 year4 year5 year6 year7 】

#表示第一行命令中的所有变量，global是全局宏

【sort state】#依据state进行排序

【foreach x of varlist $yandxforhausman{

by state:egen mean`x'=mean(`x')

gen md`x'=`x'-mean`x'

gen red`x'=`x'-theta*mean`x'

}】

#"foreach"为循环语句，对变量名单上的所有 进行同样的操作。

【quietly reg redfatal redbeertax redspircons redunrate redperinck redyear2 redyear3 redyear4 redyear5 redyear6 redyear7 mdbeertax mdspircons mdunrate mdperinck mdyear2 mdyear3 mdyear4 mdyear5 mdyear6 mdyear7, vce(cluster state)】

#用"reg"命令做辅助回归，"vce(cluster state)"处理异方差

【test mdbeertax mdspircons mdunrate mdperinck mdyear2 mdyear3 mdyear4 mdyear5 mdyear6 mdyear7】

#使用"test"命令对所有的解释变量的组内离差进行联合显著性检验
在Stata中执行Hausman test2的命令

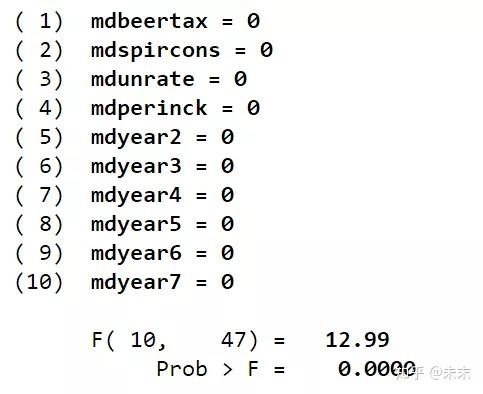
由检验结果可知，F检验的P值为0，小于0.01，所以在0.01的显著性水平下拒绝原假设，采用固定效应模型。

Hausman teat2解决了误差项存在异方差的问题，那么如果误差项存在截面相关，又该怎么办呢？

我们采用命令Hausman test3解决误差项截面相关的问题。

基于随机效应模型估计的截面相关检验

首先，因为我们构造的模型考虑了时间效应，所以通过命令【xtcsd，fre】检验误差项是否存在截面相关的问题。

由检验结果可知，1.788大于0.01显著性水平所对应的值0.7678，所以在0.01的显著性水平下拒绝原假设，认为随机效应模型的误差项存在截面相关问题，需要进行处理。

实现程序：Hausman test3 （适用于异方差和截面相关的情形）

Hausman test3只需将Hausman test2命令中的第六步进行辅助回归的代码中的"reg"命令改为"xtscc"命令即可。

【quietly xtscc redfatal redbeertax redspircons redunrate redperinck redyear2

redyear3 redyear4 redyear5 redyear6 redyear7 mdbeertax mdspircons

mdunrate mdperinck mdyear2 mdyear3 mdyear4 mdyear5 mdyear6 mdyear7】

使用"test"命令对所有的假设变量的组内离差进行联合显著性检验。

【test mdbeertax mdspircons mdunrate mdperinck mdyear2 mdyear3 mdyear4 mdyear5 mdyear6 mdyear7】

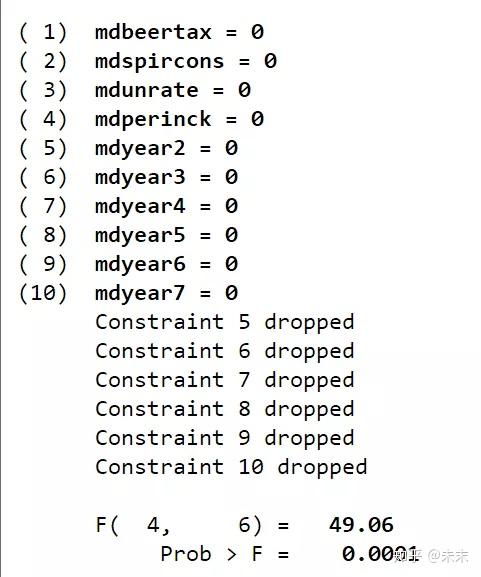
检验结果的P值为0.0001，同样拒绝原假设，所以选择固定效应模型。

第四步 报告计量结果

通过第三步模型的选择，我们最终确定了固定效应模型，所以报告固定效应模型的结果，同时我们要解决误差项可能存在的自相关、异方差和截面相关问题。

在第三步中，通过命令"xtcsd"我们识别到了误差项存在 截面相关 的问题；

接下来 ，我们检验模型 异方差问题 是否存在。

检验步骤为：

首先，我们做双向固定效应估计。

使用命令【xtreg fatal beertax spircons unrate perinck year2-year7,fe】

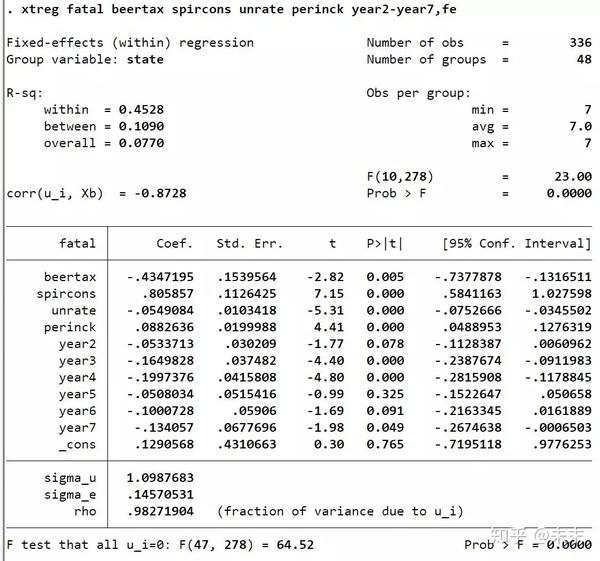
然后，我们运行【xttest3】命令

#【xttest3】只能在"xtreg,fe"或"xtgls"命令之后使用。首次使用【xttest3】的同学需要使用命令【ssc install xttest3】进行安装。

异方差检验结果显示：P值为0，所以拒绝原假设，认为存在异方差问题。

最后， 我们检验误差项的自相关问题

通过命令【xtserial】对误差项的自相关问题进行检验。

#首次使用【xtserial】的同学需要使用命令【search xtserial】进行安装。

通过命令【tab state,gen(state)】生成州的虚拟变量

然后执行命令【xtserial fatal beertax spircons unrate perinck state2-state48 year2-year7】

由检验结果可知， p=0.1134>0.01 ,所以可以认为，在0.01的显著性水平下不拒绝原假设，即认为模型不存在自相关问题

综上，由于存在截面相关和异方差问题，所以我们使用命令"xtscc"进行双向固定效应模型的估计。

使用命令：

【xtscc fatal beertax spircons unrate perinck year2-year7,fe】

【est store Driscoll-Kraay】

其中，标准误是Driscoll-Kraay，估计量是组内估计量。

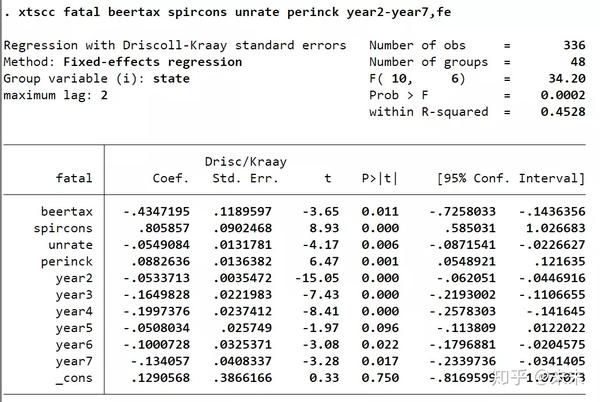
此外，如果不存在截面相关，一般最终报告由如下命令估计的结果：

【xtreg fatal beertax spircons unrate perinck year2-year7,fe cluster(state)】

【est store Rogers】

其中，标准误是Rogers或聚类稳健标准误

用robust替换cluster(state)选项会得到相同的结果

【xtreg fatal beertax spircons unrate perinck year2-year7,fe robust】

【est store White】

其中，标准误是White标准误或稳健标准误

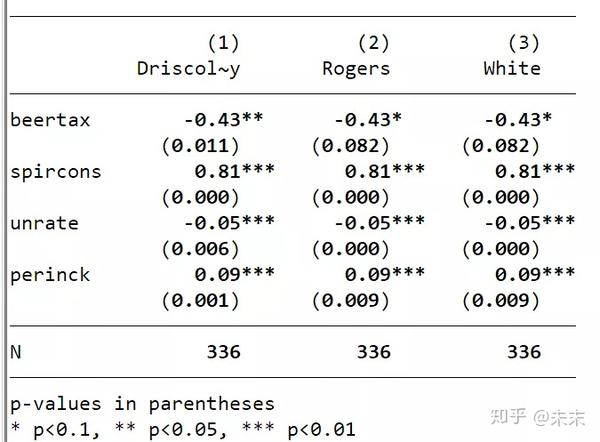
最后 ，我们可以通过"esttab"命令将所有的存储结果放在一起比较。

【esttab Driscoll-Kraay Rogers White,b(%9.2f)p mtitle(Driscoll-Kraay Rogers White)obslast star(* 0.1 ** 0.05 *** 0.01)compress nogap k(beertax spircons unrate perinck)】

#首次使用【esttab】的同学需要使用命令【ssc install estout】进行安装。