【财通金工】“拾穗”多因子（十一）：多因子风险预测：从怎么做到为什么

来源：雪球App，作者： 量化陶吧，（https://xueqiu.com/8744430809/127385502）

投资要点

► 多因子风险预测：从怎么做到为什么

样本协方差矩阵估计存在三点不足：运算大、不可逆、偏差大，基于多因子的协方差矩阵估计可以针对这些问题发挥用武之地。

最优投资组合是指在相同期望收益的条件下，具有最小波动率的资产组合。对最优投资组合权重求解的准确性主要取决于对期望超额收益的估计（一阶风险）和对协方差矩阵的估计（二阶风险）。

在收益率满足正态分布的假设下，偏差统计量衡量的是实际风险与预测风险的比值，然而金融数据往往服从“尖峰厚尾”分布，因此即便对于完美的预测方法而言，也很难做到偏差统计量等于1。

收益率分布对于偏差统计量落入其置信区间内的概率存在影响，随着收益分布的峰度逐渐变大，落入95%置信区间的概率逐渐减小。

Newey-West调整主要用于解决协方差矩阵估计中股票收益的自相关性影响，财通金工通过蒙特卡洛模拟法探究其原理。

特征值调整的主要逻辑在于通过蒙特卡洛模拟法来试图模拟出各个特征组合的偏差统计量与1之间的偏差，继而进行调整。

特质风险估计中贝叶斯压缩调整的主要思想是将单只股票的特质风险向其所在的市值分组的市值加权平均风险压缩，实证发现股票特质风险与其市值之间存在强相关关系。

►指数风险预测

所有样本指数在未来一个月的年化波动区间在23%-33%之间，相较上周出现非常明显的攀升，财通金工特别提醒投资者注意当前市场的波动情况，后市维持谨慎观点。

►指数成分收益归因

上周市场风格以大盘指数为主，表现最好的三只指数都是大盘指数，其在非线性规模因子上暴露较少，而表现较差的三只指数更多得偏向于中小市值股票，其在非线性规模因子上的较大暴露拖累指数收益。

►风险提示

本报告统计结果基于历史数据，过去数据不代表未来，市场风格变化可能导致模型失效。

► 更多交流，欢迎联系财通金工张宇，联系方式：17621688421（注明机构+姓名）

欢迎在Wind研报平台中搜索关键字“星火“和”拾穗”，下载阅读专题报告的PDF版本。

本期是该系列报告的第11期，主要就多因子模型协方差矩阵估计中的很多细节展开探讨。在财通金工“星火”专题（二）中，我们介绍了如何根据多因子模型对股票收益的协方差矩阵进行稳健估计，但对其背后各项调整的原理并未做过多涉及。在本次讨论中，我们就其中的很多细节再次进行斟酌，以期帮助投资者对基于多因子模型的协方差矩阵估计有更为深入的理解。

多因子风险预测：从怎么做到为什么

1

在财通金工“星火”多因子系列（二）《Barra模型进阶：多因子风险预测》中，我们针对传统股票收益率样本协方差矩阵估计的不足介绍了如何根据多因子模型对股票的风险矩阵进行更稳健的估计。基于结构化的协方差矩阵估计方法将股票收益协方差矩阵拆解为 共同风险矩阵和特异风险矩阵 两个部分，并对两个矩阵的估计进行了多步调整。在该篇专题研究中，我们更多的是向投资者介绍如何在模型中进行这些调整，对其背后的原理和逻辑并未做过多涉及。 作为“星火”系列的衍生报告，本期我们着重就投资者日常使用过程中的一些疑惑和模糊的细节展开讨论，介绍财通金工对多因子模型风险预测中的理解和思考 。

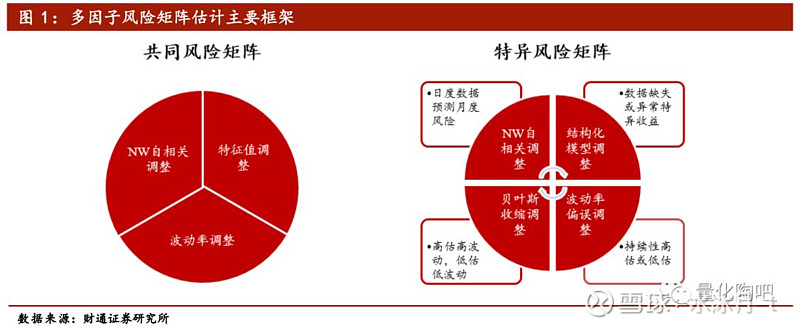
1.1  样本协方差矩阵的三个不足：运算大、不可逆、偏差大

在本文的开篇部分我们先来关注为何要采用结构化的方法对股票协方差矩阵进行估计，这主要是由于基于股票收益序列的样本协方差矩阵存在如下三点不足造成的：

首先，采用收益率的样本协方差进行估计的方法运算次数明显更大 。假如要对N只股票的协方差矩阵进行估计，那么就需要进行(N(N+1))/2次运算，而基于多因子模型的方法将N只股票替换为K个因子（其中K≪N），运算次数大大减少。当然在计算机运算能力发展到今天的时代，这样的运算次数也并非不可接受的。

其次，样本协方差矩阵通常并不可逆 。在实际应用中，协方差矩阵通常被用于组合优化和风险控制中，对协方差矩阵进行求逆便是一个通用的操作。然而当股票数量N大于样本观测长度T时，简单协方差矩阵便是一个不满秩（not full rank）的矩阵，因此不能直接对其求逆操作，这使得其在实际应用中大打折扣。

最后，基于样本协方差矩阵的估计对于最优投资组合的风险预测存在较大偏差 。Shepard（2009）指出，在正态性和平稳性的假设下，由于估计误差的存在，采用样本协方差矩阵得到的最优投资组合的风险通常会被低估，其模型估计值与真实风险之间的关系满足：

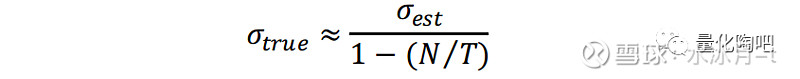
其中，σ_true表示最优投资组合的真实波动率，σ_est表示根据样本协方差矩阵估计得到的组合预测波动率，N表示股票数量，T表示样本观测数量。例如，当采用100个交易日数据来估计50只股票收益率的协方差矩阵时，最优投资组合的估计风险仅为真实风险的1/2。

为了解这一关系的由来，我们先来明晰何为最优投资组合（optimal portfolio）。所谓最优投资组合，是指在相同期望收益的条件下，具有最小波动率的资产组合。用数学语言来表示，假设α为N只股票的期望超额收益（N×1向量），Ω为股票收益协方差矩阵（N×N矩阵），w为股票的权重向量（N×1向量），那么求解w的目标函数可以表示为：

如果采用 拉格朗日乘数法 对其进行求解，首先就需要构造拉格朗日函数：

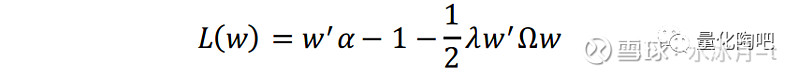
其中，λ为调节参数，为方便起见将其值取为1（注意，它的取值并不影响个股权重的相对大小）。将上式对w求偏导，即有：

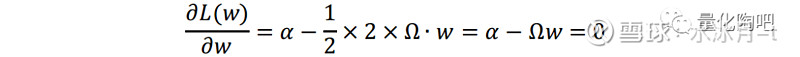
因此，最优投资组合的权重即为：

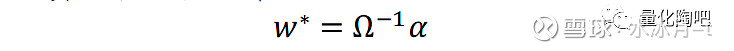
最优投资组合的风险即可以表示为：

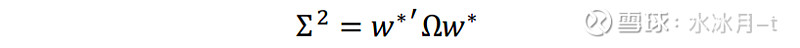
Shepard（2009）认为，如果我们知道真实的协方差矩阵Ω，那么上面的估计将会是组合风险的良好估计。然而在实际应用中，我们只能够根据样本观测值对协方差矩阵Ω的真实分布进行估计（即Ω ̂）。因此，根据估计得到的协方差矩阵Ω ̂得到的最优投资组合的权重即可表示为：

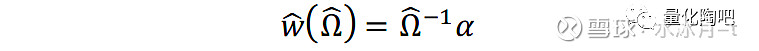
由此可见，对于最优投资组合权重求解的准确性主要源于两个部分的估计准确性，其一是关于个股期望超额收益α的估计（一阶风险），其二为对真实协方差矩阵Ω的估计，此为二阶风险（Second Order Risk）。 在传统的多因子研究中，我们更多关注对个股/组合/因子的收益预测，而忽略了对风险矩阵的估计 。

那么二阶风险的存在对于最优投资组合的风险预测准确度到底有多大的影响呢？Shepard（2009）指出，如果收益率序列平稳且满足正态分布，那么样本协方差矩阵Ω ̂将服从关于Ω的Wishart分布。根据Wishart分布的性质，即有：

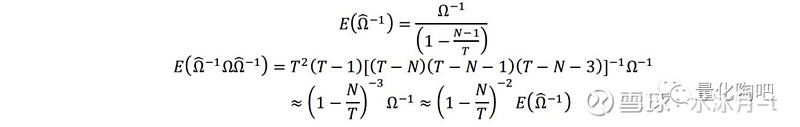
其中第二个和第三个近似分别忽略了1/N和1/T的微小影响得到的。

由此，对于最优投资组合（权重为w ̂=Ω ̂^(-1) α）而言，其预测风险可表示为：

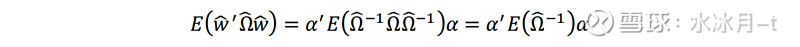
而该组合的真实风险可以表示为：

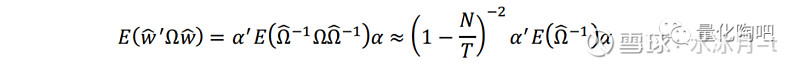
其中最后一个等式即可根据上面的推导得到。对上式两边同时取平方根，即可得到最优投资组合的实际波动与预测波动之间的比值：

证明完毕。

1.2  偏差统计量的含义及置信区间

在风险预测的研究中，我们通常采用偏差统计量来衡量风险测度的准确性。它可以通过如下两步计算得到，首先计算资产组合收益率的样本外标准化收益：

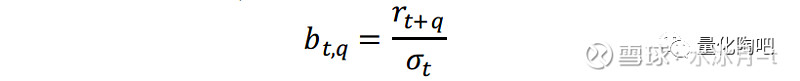
其中，σ_t表示资产在当前时刻t的预测风险，r_(t+q)表示从当前时刻t到t+q期间资产的收益率，q为预测时间长度，在我们的研究中通常将其取为21天。随后通过计算回测区间内样本外标准化收益的标准差，即为偏差统计量（bias statistics）：

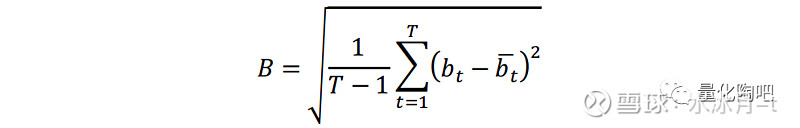
我们一直在强调偏差统计量实际上衡量的是实际风险与估计风险之间的比值。如果一个风险估计是完美的，那么它的偏差统计量应该恰好等于1。若偏差统计量大于1，则说明该组合的风险被低估；若偏差统计量小于1，则说明组合的风险被高估 。但由于历史数据有限，即便对于完美的风险估计方法其偏差统计量也未必等于1，因此在收益率的正态分布假设下，我们认为偏差统计量的95%置信区间可以表示为：

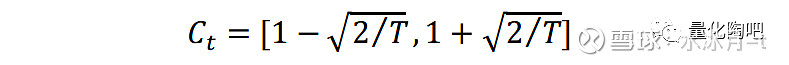
那么，为何完美风险预测方法的偏差统计量会等于1？为何偏差统计量衡量的是组合实际风险与预测风险之间的比值？偏差统计量的95%置信区间又是如何计算得到的呢？本部分财通金工试图介绍一下我们自己的思考。

假设收益率序列r_t服从均值为μ，标准差为σ_t的正态分布：r_t~N(μ,〖σ_t〗^2)，那么对于一个准确估计其风险的测度σ_t而言，其样本外标准化收益应该服从如下正态分布 ：

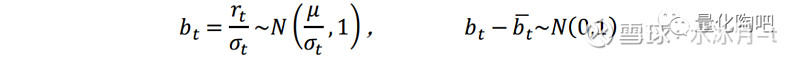
因此，如果风险测度是准确的，那么该样本外标准化收益b_t的标准差——偏差统计量应该等于1。同时我们也可看到，由于b_t-(b_t ) ̅服从标准正态分布，因此统计量(T-1) B^2应该服从自由度为T的χ^2分布 ：

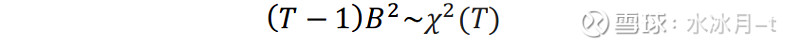
因此，偏差统计量B的95%置信区间即可表示为：

根据χ^2分布的特征，其95%置信区间可以近似地表示为：

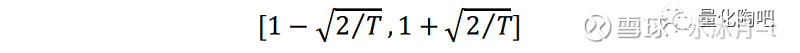
需要特别注意的是，此处的T并非波动率估计时回望的时间长度，而是回测区间内样本外收益序列的长度 。例如当采用过去126天的日度收益的标准差来估计股票的日度风险时，若连续进行252天滚动估计，那么此时T的取值应为252。此时，95%置信度区间即可表示为：

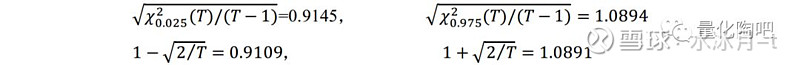
可以看到二者之间是非常近似的。

1.3  收益分布对偏差统计量的影响

在上一小节中我们所有关于偏差统计量的假设检验都是基于 收益率分布服从正态分布 的假设之上所做出的，然而现实中的股票收益率序列并不服从正态分布，而是服从“尖峰厚尾”分布，这也导致即便对于完美的风险预测方法来讲，采用现实数据的拟合并不一定就有95%的数据能够落在95%置信区间以内，本小节我们就来探讨 收益率的不同分布对于偏差统计量能够落在95%置信区间内概率的影响 。

财通金工采用蒙特卡洛模拟法分别生成三个时间序列：a）均值为0，方差为0.2/252的正态分布；b)自由度为7的t分布；c)自由度为6/7+4的t分布。由于正态分布的偏度等于3，而t分布的偏度与其自由度v存在如下关系：

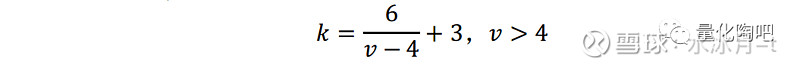
因此，以上三个收益率序列的峰度分别为a) k=3； b) k=5； c) k=10。对于每一个观测区间长度T（再次强调，此处的T并非指计算标准差时回望的天数），我们统一采用过去252天的滚动收益标准差作为第二天波动的预测值，对于每一个T值我们进行1000次蒙特卡洛模拟，它们分别对应1000个偏差统计量，最后再计算出这1000个偏差统计量落在[1-√(2⁄T),1+√(2⁄T)]置信区间中的比例。

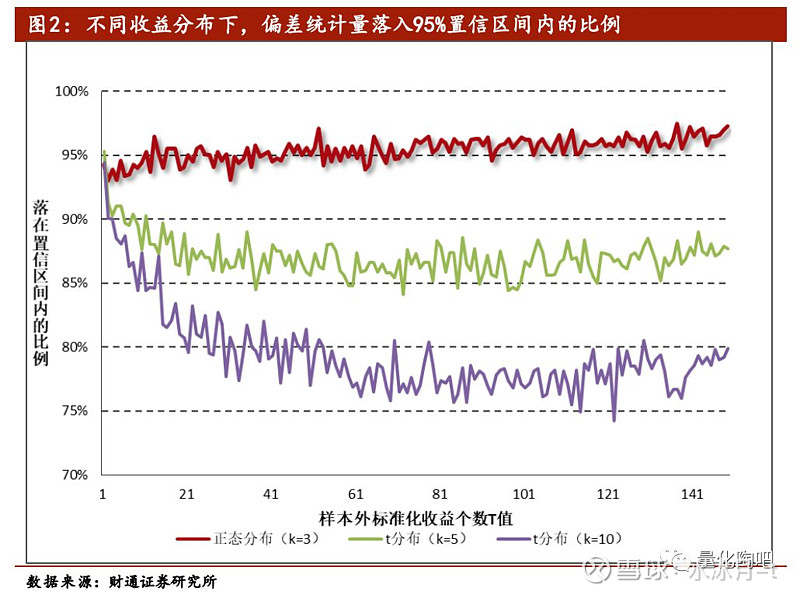图2展示了不同收益分布下，偏差统计量落入95%置信区间内的比例。可以看到，如果收益率序列服从正态分布（k=3），那么对于所有的T值而言，偏差统计量落入到95%置信度区间内的比例基本在95%左右，这一点显然是合意的。随着收益分布的峰度逐渐变大，偏差统计量落入95%置信区间内的比例逐步变小，对于k=5的分布其均值在87%左右，对于k=10的分布其均值大概在80%左右。

由此我们认为，由于现实金融数据并不服从正态分布，我们应该允许计算得到的偏差统计量与95%置信区间存在一定的偏离，而不能对其结果过于苛求。

1.4  指数移动加权平均EWMA调整

在将基本概念厘清后，我们开始讨论不同调整方法背后的逻辑 。本部分我们先来关注共同风险矩阵的估计，传统的样本协方差矩阵估计法对所有数据点赋予相同的权重，然而由于市场变化较快且我们采用的历史数据较长，而近期数据对当前状态的影响比早期数据更大，因此我们采用指数移动加权平均（Exponentially Weighted Moving Average）的方法，对近期数据赋予更大的权重以增加它们对当前数据状态的影响，从而能够更及时地反映市场变化。在财通金工研究过程中，我们发现不少投资者对于 半衰权重的计算 存在疑虑，因此本部分我们对此进行较为详尽的阐述。

对于给定的一个T×1维收益率序列，采用简单的样本方差法计算其波动即是将收益率与其样本均值相减，再将其进行点乘并计算平均值，这实际上暗含着每个数据样本点的权重均为1/T的约束。然而对于半衰指数加权移动平均而言，我们假设当前时刻为t时刻，历史数据样本点（由远及近）分别为：

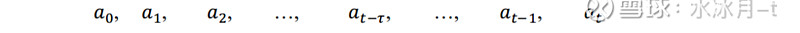
那么这些样本点对应的权重可以表示为：

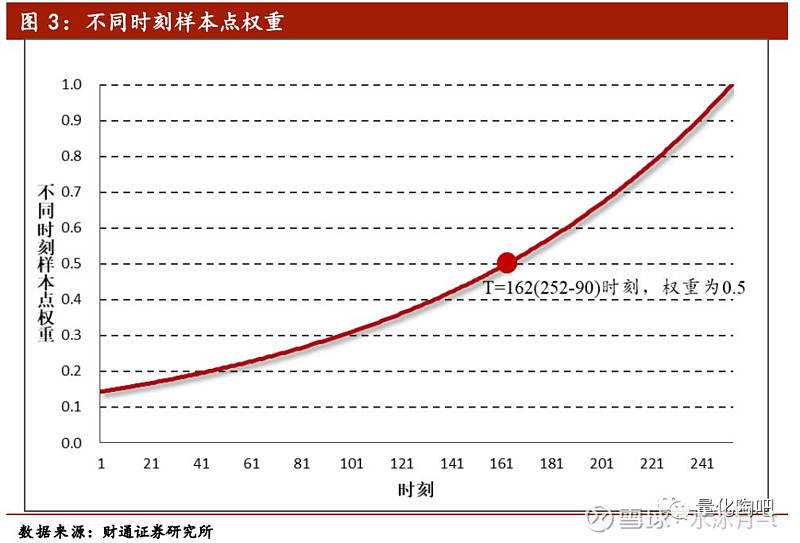
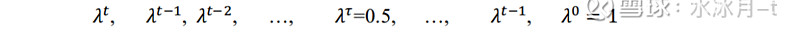其中，λ=0.5^(1/τ)，τ为半衰期参数，它表示第 t-τ天的样本数据权重为当前日权重的1/2（此处我们先假定当前日的数据权重为1，之后再进行归一化）。图3展示了当h取252天,半衰期取90天的时候，各个样本点的权重示意图。可以看到，当前时刻的数据权重为1，当前时刻往前推90天时刻的样本点权重即衰减为当前的一半，这也就是“半衰”本身所代表的含义。需要注意的是，在最后计算的时候还需要对权重进行归一化，使得所有样本点权重之和等于1。

要了解上式是如何推导的，我们首先来了解一下指数移动加权平均的含义，它在机器学习相关研究中也是非常基础的内容。假设a_k表示第k个数据，且a_0=0，那么 当前数据的取值即为历史数据与当前数据的加权平均 ，权重用β表示：

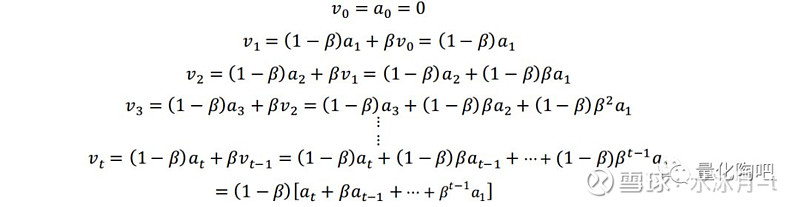
我们一般我们取β≥0.9，由等比数列的性质可知，当t趋向于无穷大的时候，所有数据的权重之和加起来趋近于1：

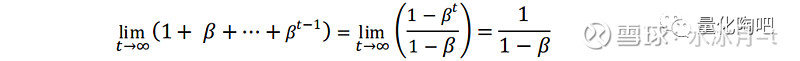由上式可以看到，对于t-n天的数据，其权重为β^n（暂时先忽略1-β的系数）如果我们取半衰期为τ天，也就是说第t-τ天的样本数据权重为当前日的1/2，那么即有β^τ=1/2，因此β=〖0.5〗^(1/τ)，这一点恰好与我们前面提到的λ值的计算完全相同。

在了解了各个样本数据点的权重之后，我们即可根据协方差的定义计算半衰指数加权平均处理过后的协方差矩阵。

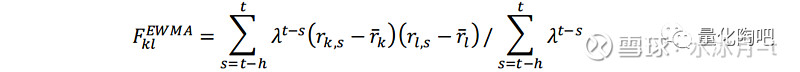
其中，r_(k,s)表示因子k在s期的收益，r ̅_k表示因子k的收益在样本期内的指数加权平均，h为样本时间长度。 财通金工特别提醒投资者注意的是，在计算样本均值时需要计算指数加权平均而非简单平均，否则不能保证计算得到的协方差矩阵为半正定矩阵，从而影响后续特征值和特征向量的求解 。

1.5  Newey-West调整

样本协方差矩阵在经过指数加权移动平均处理后，下一步即进行Newey-West调整。 持续关注财通金工多因子研究的投资者会看到，Newey-West调整不仅能够在多因子风险矩阵的自相关调整中发挥作用，后续还会频繁地出现在多因子选股研究中的因子有效性假设检验中 ，因此对这一步调整背后逻辑的理解十分必要，我们在本小节中对其进行探讨。

Newey-West调整主要用于解决协方差矩阵估计中，数据的自相关性对数据协方差造成的影响。 由于我们通常要对较长时间（如1个月）的风险进行预测，而我们之前的估计是采用股票日度收益数据来进行计算的，因此由日度数据转换成月度数据的时候就需要考虑到数据的自相关性 ，Newey-West调整在这一步的时候就发挥了其作用，具体来讲：

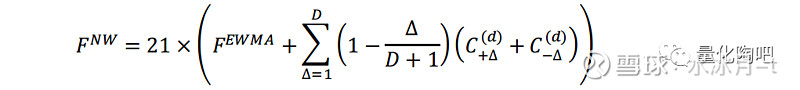
其中，F^EWMA是根据日度数据经EWMA调整后计算得到的样本协方差矩阵，D表示总的滞后时间阶数，C_(+∆)^((d))表示的是t期数据与t-∆期数据之间的协方差，其具体关系如下：

由上述公式可以很直观地看到，F_kl^EWMA衡量的是t时刻因子k收益与t时刻因子l收益之间的协方差（步调一致），而C_(kl,+∆)^((d))主要衡量的是t-∆时刻因子k收益与t时刻因子l收益之间的协方差（步调相差∆阶），这也是Newey-West调整之所以可以处理序列自相关性的关键原因，很容易可以看到C_(+∆)^((d))和C_(-∆)^((d))矩阵互为转置矩阵。为了更加直观地理解序列自相关性给序列协方差计算带来的影响，我们仍然采用蒙特卡洛模拟的方法来进行说明。为理解的方便，我们以方差的计算为例进行说明，协方差的计算原理完全相同。假设一个服从正态分布N(0, 0.2^2)的日度收益序列，那么的波动率即为0.2。假设新生成的序列存在一阶自相关性，且自相关系数为0.9，那么新生成的序列即可以表示为：

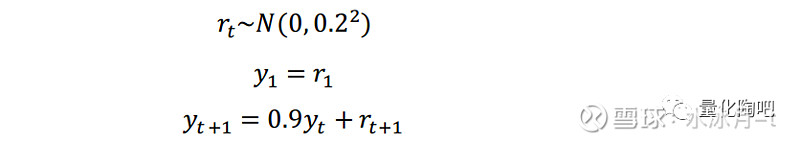
图4展示了我们随机生成的序列y_t中的其中一条，可以看到存在非常明显的自相关性：当上期数据较大时，下期数据也倾向于更大；当上期数据较小时，下期数据也倾向于更小。与我们模型中日度收益扩展为月度收益相类似的，我们可以认为是我们可以观察到的日度收益数据，而是我们观察不到的月度收益数据。我们在实际计算中，仅可计算出的波动率（接近0.2），但是我们模拟生成的的波动率却远大于0.2。

现在我们来进行1000次模拟，每一次模拟过程中我们生成的r_t和y_t序列均为1000×1维向量，并且维持r_t服从 N(0, 0.2^2 )的分布。每次模拟过程中，我们可以计算生成的y_t序列的波动率，其结果如图5中的横坐标所示。如果我们只根据观测得到的r_t计算方差，那么得到的方差估计应该仅在0.2上下波动，这样的拟合效果就会变得很差。但是根据Newey-West调整方法，对序列的自相关性进行调整后，计算得到的波动率与序列真实的波动率之间的拟合效果就非常好了。实际上，图5中我们取D=1对其进行NW调整，二者之间的相关系数达到了0.99。

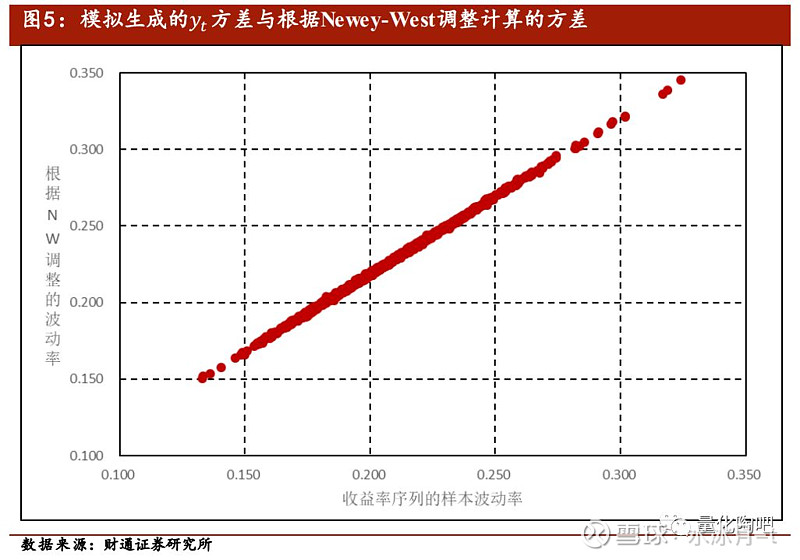
最后需要说明的一点是，Newey-West对于协方差矩阵估计中自相关调整的最大贡献在于估计中权重（或叫核函数）(1-∆/(D+1))的引入，正是由于这一权重的引入确保了估计出来的协方差矩阵仍然是一个半正定矩阵。

1.6  特征值调整的逻辑和原理

在共同因子风险矩阵中，特征值调整（Eigenfactor Risk Adjustment）是最关键也最为有效的一步。特征值调整主要针对样本协方差矩阵 低估样本内低风险组合波动、高估样本内高风险组合波动 的问题，同时对最优投资组合的风险预测也能起到有效的调整，其详细操作可参见财通金工“星火”系列（二）《Barra模型进阶：多因子风险预测》，本文仅就其背后的原理进行阐述。

所谓样本协方差矩阵“低估低波动、高估高波动”问题，即是指样本协方差矩阵对样本内低波动特征组合的未来波动预测存在明显低估、对样本内高波动 特征组合 的未来波动预测存在明显高估的问题。具体来讲，对简单样本协方差矩阵进行特征值分解，即有：

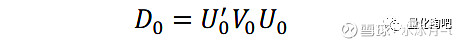
其中，U_0是一个N×N的正交矩阵，U_0的第k列即为第k个特征组合的权重向量，其满足权重平方和等于1的约束，且第k个特征组合的样本内波动即为对角矩阵D_0中对角线上第k个元素的平方根。 如果D_0中对角线上元素是由小到大进行排列的，那么U_0中第1列对应的特征组合可被认为是满足资产组合权重平方和等于1的所有组合中波动率最小的组合，而第N列特征组合即是满足资产组合权重平方和等于1的所有组合中波动率最大的组合 （Menchero，2011）。

现在我们再来深入了解一下特征值分解的含义，这一步对于后续蒙特卡洛模拟部分的理解非常重要。根据协方差矩阵的计算公式：

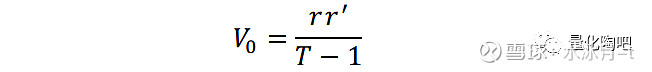
其中，r表示股票的日度收益率矩阵（N×T）。如果我们将D_0也视为N只股票收益率序列f的协方差矩阵，那么这N只股票的收益率序列之间应该满足互相正交、且第k只股票的收益率方差即为D_0对角线上第k个元素：

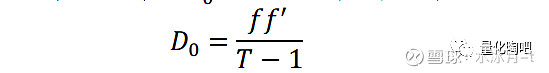
由此，我们有：

由于U_0为正交矩阵，因此其转置的逆矩阵即为矩阵本身。因此， 原始股票的收益率矩阵r可以表示为N只收益率序列相互正交的股票收益矩阵f经过特征向量矩阵U_0旋转而得到的 ：

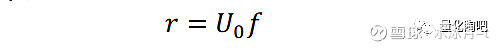
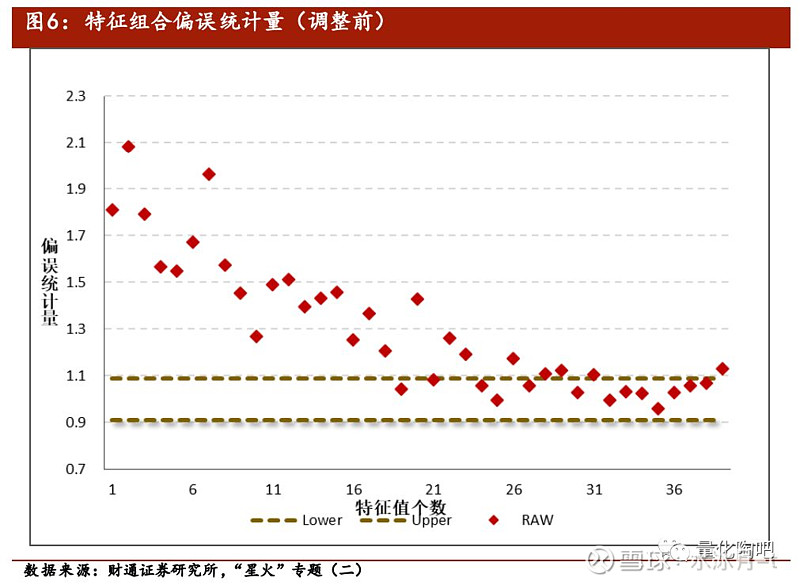
图6将所有特征组合的样本内风险由小到大进行排列，绘制出各个特征组合的偏差统计量。可以看到，对于样本内低波动的特征组合（偏左侧组合）而言，其偏差统计量明显大于1；而对于样本内高波动的特征组合（偏右侧组合）而言，其偏差统计量则更接近于95%置信区间以内。由此，我们即需要对样本协方差矩阵进行特征值调整，以尽可能地消除这一影响， 而调整的目的即是通过蒙特卡洛模拟的方法来试图模拟出各个特征组合的偏误统计量到底与1之间存在多大的偏差 。具体来讲：

首先对样本协方差矩阵V_0进行特征值分解，得到特征矩阵U_0和特征值矩阵D_0。此处我们 先假设样本协方差矩阵V_0即为真实的协方差矩阵 ，那么我们可以通过蒙特卡洛模拟随机生成一组收益率序列f_m（N×T矩阵），其每一行服从均值为0，方差为D_0对应的对角线元素的正态分布。由于f_m的每一行之间没有相关性，因此可以认为它们互相之间是正交的。由此，将特征向量权重与收益率序列相乘，即可得到组合的收益率序列：

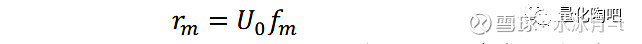
我们先来理解一下f_m和r_m分别代表什么含义。 我们可以将每一个特征因子组合看作是一只股票，那么根据特征因子组合的样本内方差生成的收益率矩阵f_m的第k行即可看作是第k只股票在每一个时刻的收益率序列，且这些收益率序列之间是互相正交的。由前面的分析可以知道，将这N只股票的收益率序列经过特征值矩阵U_0进行旋转，即可认为得到了原始N只股票的收益率序列r_m 。对模拟生成的原始个股收益率矩阵r_m（N×T矩阵）计算其样本协方差V_m，即可得到原始矩阵V_0的无偏估计：

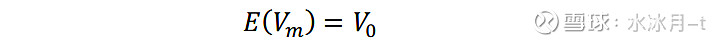
这是因为：

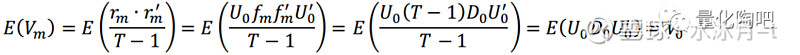
对模拟生成的样本协方差矩阵进行特征值分解，即有：

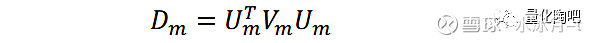
其中，U_m表示模拟生成的特征因子组合，这些特征因子组合的预测风险即为D_m。由于我们前述假定了V_0即为我们已知的真实风险，因此这些特征因子组合的“实际风险”可以表示为：

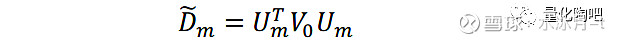
因此， D ̃_m对角线上的元素与D_m对角线上的元素的比值即为模拟特征因子组合的实际风险与预测风险之间的偏差 ，如果该偏差显著大于1说明低估了组合的未来风险，因此要对协方差矩阵的值进行放大；如果该偏差显著小于1，说明高估了组合的未来风险，因此要对协方差矩阵的值进行缩小。

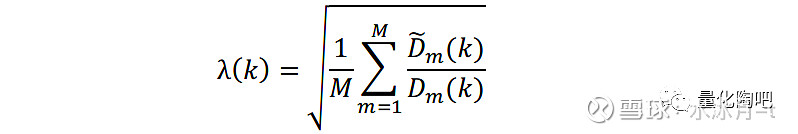
其中，M表示模拟的次数，λ(k)即反映出第k个特征组合的真实风险与预测风险之间的比值，即模拟偏差。

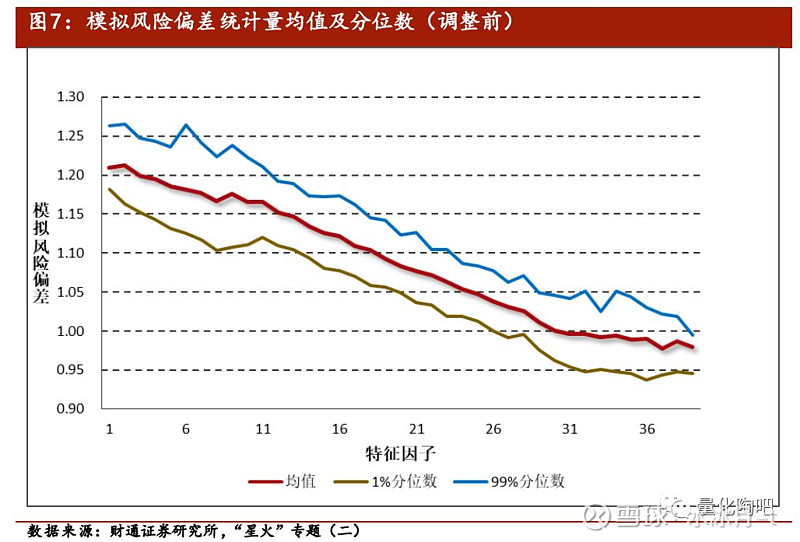
图7反映了调整前的模拟偏差的均值及1%和99%分位数，可以看到其分布基本与特征组合的偏误保持一致。 通过对低估组合的风险进行适当放大、对高估组合的风险进行适当缩小，即可得到更为准确的协方差矩阵 。图8和图9分别展示了调整后的特征组合偏差统计量和最优投资组合的偏差统计量，可以看到特征值调整的效果十分明显，调整后的组合偏差统计量基本落在了95%置信区间以内。

1.7  特质风险结构化模型调整

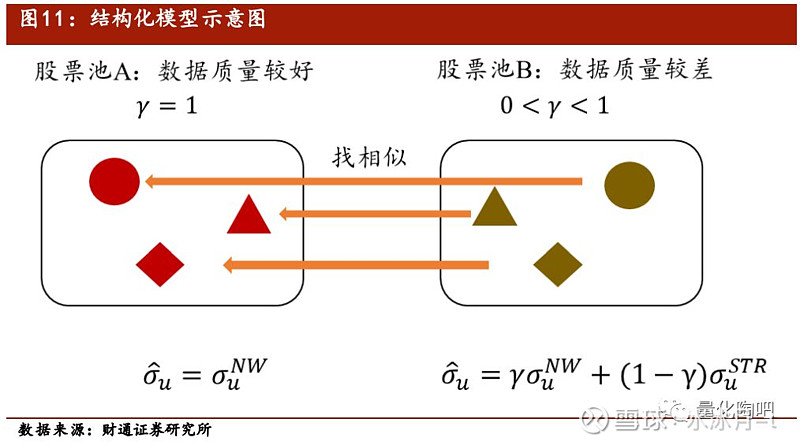
在特质风险的计算中，我们假定股票特质风险与共同因子风险互不相关，且股票与股票之间的特质风险互不影响，因此单只股票的特质风险全由其历史特质收益序列计算得到。 然而对于上市不久、长期停牌和存在较大异常值的特质收益序列来讲，直接采用特质收益的历史波动率进行拟合将存在较大的问题，结构化模型（Structural Model）的引入正是用于解决数据存在缺失值和异常值的问题。

首先我们来看如何分辨数据质量的好坏，这主要是由协调参数γ来衡量，具体来讲：

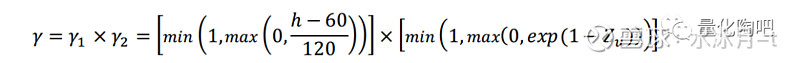
其中，h表示历史区间内股票特质收益存在数据（即不存在缺失）的个数。很容易看到，γ是一个0-1之间的参数，它用于衡量数据质量的优劣。 γ值越接近于1说明数据质量越好，γ值越接近于0说明数据质量堪忧 。其中γ_1用于衡量数据完整度，如果过去252个交易日内有至少180个交易日有特质收益值（h≥180时），说明数据较为完整，γ_1值为1。同样的，γ_2用于衡量数据异常值的存在对数据质量的影响，Z_u用于衡量特质收益的肥尾程度，当Z_u≤1时，说明数据异常值的存在对数据的影响不大，γ_2=1。现在我们来看一下该指标的计算方法：

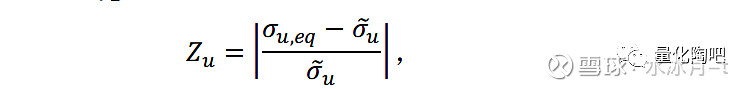
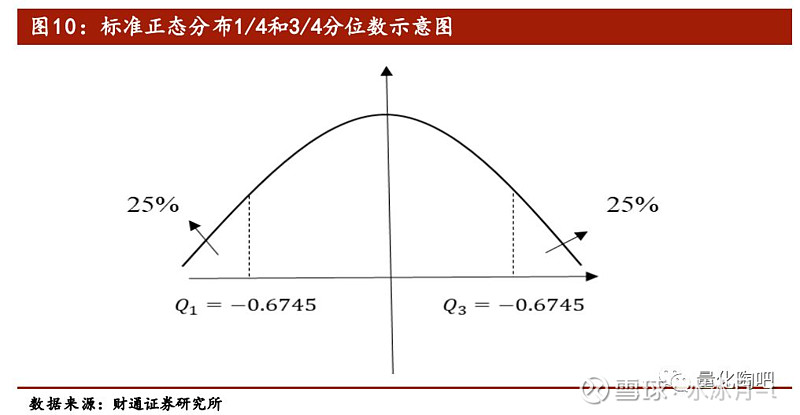
其中，σ ̃_u=(1⁄1.35)*(Q_3-Q_1 )是指特质收益的稳健标准差，Q_3和Q_1分别表示该股票特质收益序列的3/4和1/4分位数。 之所以将两个分位点之差除以1.35作为序列的稳健标准差，是因为对于标准正态分布N(0,1)而言，其3/4分位数和1/4分位数分别为0.6745和-0.6745，二者的差值接近于1.35 。假设时间序列服从正态分布N(μ,σ^2)，那么通过如上方法计算得到的稳健标准差即为σ。

当序列中存在异常值时，由于分位数对异常值相对没有那么敏感，因此序列的稳健标准差不会改变太大，而对于序列的简单标准差而言就会显著地增大。当简单标准差σ_(u,eq)远大于稳健标准差σ ̃_u时，说明序列中存在较多异常值，此时Z_u将会显著大于1，从而导致γ_2小于1。另外值得注意的是，由于指数函数的值域永远是大于0的，因此γ_2的计算中(max)┬ (0,exp(1-Z_u))的表示方法实际上是略显累赘的， 财通金工猜想之所以这样表示，是为了在形式上与前一部分的格式保持一致 。

在根据γ系数将全样本数据划分为数据质量较好和数据质量较差的两个样本池之后，接下来的工作即对数据质量较差的股票特质风险进行结构化填充，其主要思想是 对于数据质量较差的股票A而言，在数据质量较好的股票池中找到与该股票具有相似特征的股票B，并将A股票的特质风险向B股票的特质风险靠拢 。这种结构化是思想同样可以应用到数据缺失值的填充中，财通金工在“拾穗”系列（6）《因子缺失值处理：数以多为贵》中对此有详细介绍，感兴趣的投资者可以参考阅读。

1.8  特质风险贝叶斯压缩调整

贝叶斯压缩调整（Bayesian Shrinkage），是针对经指数移动平均、Newey-West调整以及结构化模型调整过后的矩阵对样本外特质风险存在“高估高波动、低估低波动”问题的修正。实际上，除了基于多因子模型的协方差矩阵估计之外，Ledoit和Wolf（2003）两位学者相继提出的各种基于收益率序列的压缩矩阵估计法也是实际投资者使用比较广泛且计算相对简便、效果较好的方法（以下简称LW方法），他们的估计方法也就是将简单样本协方差矩阵向先验协方差矩阵进行压缩，从而得到协方差矩阵的稳健估计。因此本小节我们针对多因子模型中的贝叶斯压缩调整进行简要介绍， 在财通金工的后续研究中我们还将陆续探讨基于多因子模型的协方差矩阵估计以及基于Ledoit和Wolf提出的压缩矩阵估计之间的优劣比较，欢迎感兴趣的投资者持续关注 。

LW方法是将样本协方差矩阵Σ_Sample和目标风险矩阵（或先验风险矩阵）Σ_Target的线性组合作为协方差矩阵的稳健估计：

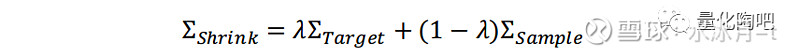
其中，0

在多因子模型的贝叶斯收缩调整中，其 主要思想是将单只股票的特异风险向其所在的市值分组的市值加权平均风险压缩 。

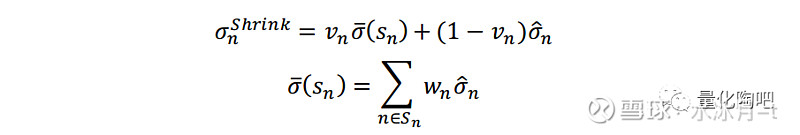
其中，σ ̅(s_n )即为贝叶斯先验风险矩阵（也就是上面提到的目标风险矩阵或者压缩目标矩阵），它表示股票所在的市值分组的市值加权平均，v_n为压缩密度。

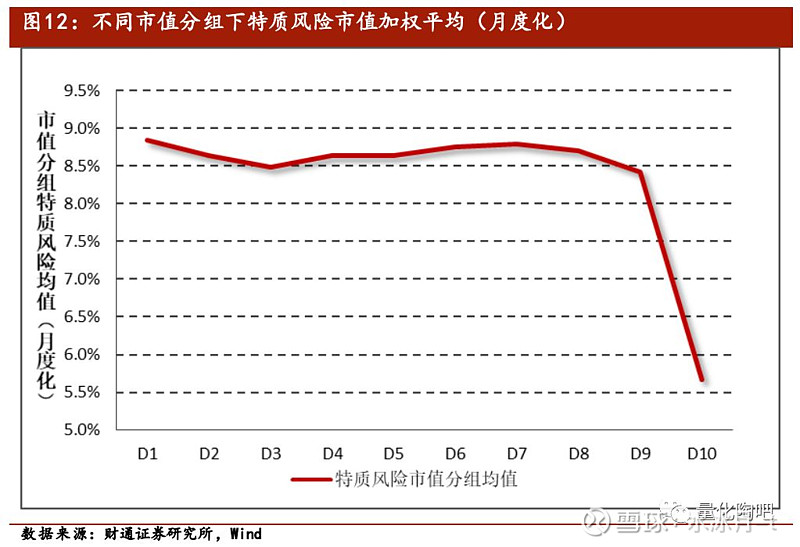
所谓先验风险矩阵，即是指在给定任何其他附加条件之前，凭借我们主观的认知，我们认为单只股票的特质风险将会更加接近于哪些值。因此，如上的调整事实上隐含了 股票的特质风险与其市值存在着强相关性的假定。正是因为具有相似市值的股票的特质风险将更为接近，我们才会将个股的特质风险向其所在的市值分组平均靠拢 。图12展示了回测区间段内，不同市值分组下的特质风险市值加权平均，其中D1表示市值最小的分组，D10表示市值最大的分组。可以看到市值最大的前面两组的特质风险明显更小，而D1-D8组之间的分化则没有那么明显。

最后我们讨论一下 压缩密度v_n的估计，它衡量的是个股特质风险与其所在的市值分组中的市值加权特质风险均值的偏离程度 。如果个股特质预测风险越偏离其所在的市值分组平均风险时，压缩密度v_n将会越大，压缩后的预测风险将更多地向其先验风险σ ̅(s_n )靠拢：

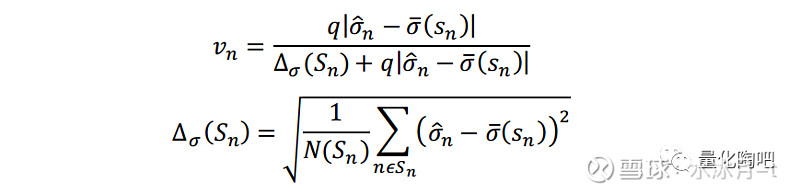
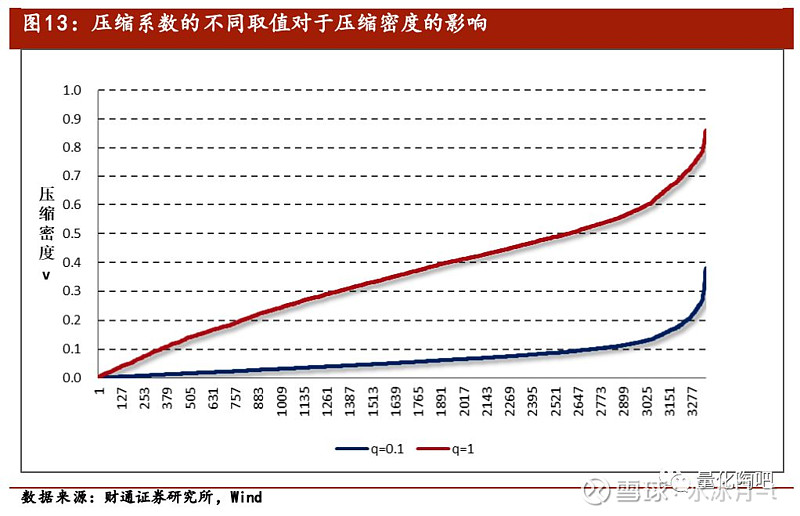
其中，q为压缩系数，通常根据经验对其进行赋值。在“星火”系列（二）《Barra模型进阶：多因子风险预测》中，我们将其值置为1，但是在Barra USE4文档中，该值取的是0.1。那么对于该值究竟如何设置呢？我们通过q值的选取对于压缩密度v_n的取值影响作为参考。

图13展示了当q值分别取为0.1和1的时候，对于某一个截面期所有股票的压缩密度v_n值的取值影响，此处我们将股票的压缩密度由小到大进行排序，可以看到q取值为1时，同一股票的v_n值明显要比q取0.1时更大。当q取0.1时，v_n值最大为0.4，而q取1时，v_n最大达到了0.85。 由于v_n值衡量的是先验风险矩阵所占的权重大小，我们认为股票的特质风险还是应该更多地取决于根据自己的历史数据计算得到的数据，而非结构化的市值加权平均数据 ，因此v_n的取值应当适当地小一点，所以q取0.1值也有其合理的解释。

1.9  小结

本期“拾穗”系列专题，我们就多因子模型协方差矩阵估计中的很多模糊的细节展开探讨，主要结论如下：

1） 样本协防差矩阵估计存在三点不足：运算大、不可逆、偏差大，基于多因子的协方差矩阵估计可以针对这些问题发挥用武之地；

2） 最优投资组合是指在相同期望收益的条件下，具有最小波动率的资产组合。对最优投资组合权重求解的准确性主要取决于对期望超额收益的估计（一阶风险）和对真实协方差矩阵的估计（二阶风险）；

3） 在收益率满足正态分布的假设下，偏差统计量衡量的是实际风险与预测风险之间的比值。然而由于金融数据服从“尖峰厚尾”分布，因此即便对于完美的预测方法而言，也很难做到偏差统计量等于1；

4） 收益率的分布对于偏差统计量落入其置信区间内的概率存在影响，随着收益分布的峰度逐渐变大，落入95%置信区间的概率逐渐减小；

5） 基于多因子的写方差矩阵估计可以分为共同风险矩阵和特异风险矩阵的估计，前者要经过自相关、特征值和波动率偏误调整，后者要经过自相关、结构化、贝叶斯压缩和波动率偏误调整几个步骤；

6） Newey-West调整主要用于解决协方差矩阵估计中股票收益的自相关性，财通金工通过蒙特卡洛模拟法探究其原理；

7） 特征值调整的主要逻辑在于通过蒙特卡洛模拟法来试图刻画各个特征组合的偏差统计量与1之间的偏差，并根据这一偏差进行放大或缩小调整；

8） 特质风险中贝叶斯压缩调整的主要思想是将单只股票的特质风险向其所在的实质分组的市值加权平均风险压缩，实证检验发现股票特质风险与其市值之间存在强相关关系，市值越大，股票的特质风险越小。

（后续章节具体内容可参见报告PDF版本）

风险提示

5

本报告统计结果基于历史数据，未来市场可能发生重大变化。

报告原文地址及相关报告

原始报告：

证券研究报告： “拾穗”多因子系列（十一）：《多因子风险预测：从怎么做到为什么》

发布时间：2019年5月7日

分析师：陶勤英 SAC证书编号：S0160517100002

联系人：张宇 17621688421

下载地址：

链接： 网页链接 提取码：o5zc

欢迎在Wind研报平台中搜索关键字“星火“和”拾穗”，下载阅读专题报告PDF版本

“星火”系列专题报告：

“星火”多因子系列（一）：Barra模型初探：A股市场风格解析

“星火”多因子系列（二）：Barra模型进阶：多因子模型风险预测

“星火”多因子系列（三）：Barra模型深化：纯因子组合构建

“星火”多因子系列（四）：基于持仓的基金业绩归因：始于Brinson，归于Barra

“拾穗”系列专题报告：

“拾穗”多因子系列（一）：带约束的加权最小二乘拟合：一种解析解法

“拾穗”多因子系列（二）：你看到的不一定是你所想的：解密R方

“拾穗”多因子系列（三）：行业因子选择：中信一级还是申万一级？

“拾穗”多因子系列（四）：总市值、流通市值、自由流通市值：谈谈取舍

“拾穗”多因子系列（五）：数据异常值处理：比较与实践

“拾穗”多因子系列（六）：因子缺失值处理：数以多为贵

“拾穗”多因子系列（七）：从纯因子组合的角度看待多重共线性

“拾穗”多因子系列（八）：非线性规模因子：A股市场存在中市值效应吗？

“拾穗”多因子系列（九）：牛市抢跑者：低Beta一定代表低风险吗？

“拾穗”多因子系列（十）：行业的风格偏好：解析纯行业因子组合

法律声明

根据《证券期货投资者适当性管理办法》（2017年7月1日正式实施），本订阅号发布的观点和信息仅供 财通证券 专业投资者参考，完整的投资观点应以财通证券研究所发布的完整报告为准。若您并非专业投资者，请勿订阅或转载本订阅号中的信息。若您并非财通证券客户中的专业投资者，为控制投资风险，请取消订阅、接收或使用本订阅号中的任何信息。

本订阅号旨在沟通研究信息，分享研究成果，所推送信息为“投资参考信息”，而非具体的“投资决策服务”。本订阅号推送信息仅限完整报告发布当日有效，发布日后推送信息受限于相关因素的更新而不再准确或失效的，本订阅号不承担更新推送信息或另行通知义务，后续更新信息请以有关正式公开发布报告为准。

市场有风险，投资需谨慎。在任何情况下，本订阅号中的信息所表述的意见并不构成对任何人的投资建议，订阅人不应单独依靠本订阅号中的信息而取代自身独立的判断，应自主做出投资决策并自行承担投资风险。本资料接受者应当仔细阅读所附各项声明、信息披露事项及相关风险提示，充分理解报告所含的关键假设条件，并准确理解投资评级含义。在任何情况下，信息发布人不对任何人因使用本订阅号发布的任何内容所引致的任何损失负任何责任。