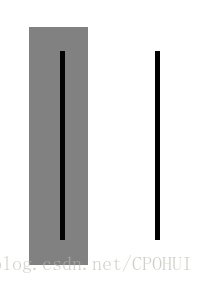今晚,老师讲了一道归纳题(”男生性别保卫战“),让我们来找出破绽。
证明:命题P班上所有同学都是女生(手动‘惊恐’,当然这是不可能的啦)。
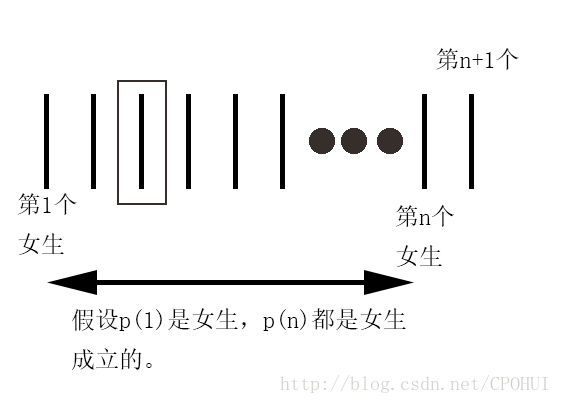
通常来讲,用数学归纳法证明步骤,第一步就是假设n=1时,第一个人是女生。设当n=k时,P(k)都是女生成立。那么接下就是证明n=k+1的成立了。这个证明的诡异之处在于,推理貌似都没有问题,请看下图:
其实,有一个误区,我们一直想证明n=k+1成立,却都没有去注意n=1人的情况,当n=1,那么k+1就等于2,此时你就已经无法证明k+1的正确性了,因为(看下图)
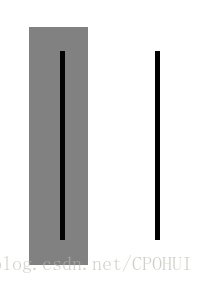
当只有两个人时,k+1已经失去了参照的人,已经无法证明k+1的正确性了(只有P(k)),所以接下去的证明都变得毫无意义。
小结
:采用归纳法证明一定要多注意起始条件,不然就有可能证明错误的结论,出现诡辩。
版权声明:本文为博主原创文章,转载请注明出处!
今晚,老师讲了一道归纳题(”男生性别保卫战“),让我们来找出破绽。 证明:命题P班上所有同学都是女生(手动‘惊恐’,当然这是不可能的啦)。 通常来讲,用数学归纳法证明步骤,第一步就是假设n=1时,第一个人是女生。设当n=k时,P(k)都是女生成立。那么接下就是证明n=k+1的成立了。这个证明的诡异之处在于,推理貌似都没有问题,请看下图: 其实,有一个误区,我们一直想证明n=k+1成立,却都没有
我很想闲下来把《What Is Mathematics》看完,但平常没有多少时间,前两天晚上睡前看了几页,正好看到Mathematical Induction,也就是数据
归纳法
,发现它很合适用来
证明
,例如我常见的等差、等比、以及平方、立方数列的求和公式。
靠着一个初始条件以及递推就可以完成
证明
,但它不能解决的问题是,如何得到这些求和公式,它只能去
证明
,没有办法得到。书里也说了要如何得到这些公式就需...
先来回忆一个小故事:高斯8岁的时候快速计算连续自然数的和。
咦!你感觉无聊了没:竟然有是这个故事,小时候都不知道听多少遍了。
其实过去这么久了,很多小时候我们耳熟能详的名字,现在对他们及他们的事迹印象没那么深了。
比如罗盛教、高士奇、齐白石、李星华等,多年不说,这样小学课本里的名字就...
数学
归纳法
(mathematical induction)是一种
数学
证明
方法,常用于
证明
命题(命题是对某个现象的描述)在自然数范围内成立。随着现代
数学
的发展,自然数范围内的
证明
实际上构成了许多其他领域(比如
数学
分析)的基础,所以
数学
归纳法
对于整个
数学
体系至关重要。
数学
归纳法
本身非常简单。如果我们想要
证明
某个命题对于自然数n都成立,那么:
第一步
证明
命题对于n = 1成立。
第二步 假设命
n阶行列式展开式:
其中,Aij = (-1)^(i+j) *Mij, Aij称为n阶行列式Dn的代数余子式,而Mij则为n阶行列式Dn去掉第i行第j列的元素后剩下元素所构成的行列式。
(3)特殊行列式归纳:
1.对角行列式:只有在对角线上有元素,且不全为0,这样的行列式我们称为对角行列式。
对角行列式的计算:为对角线的所...
解决CentOS7 重启网卡出现Failed to restart network.service: Unit network.service not found.
北凉-徐凤年:
【算法】快速排序 —— 三数取中法
小时候可白le:
重新安装Ubuntu后出现failed to download package files错误
reset6893:
(转载)Java父类异常与子类异常之间的捕获关系
llsydn: