世界上存在完美的圆吗?
来源:雪球App,作者: 大数据实验室,(https://xueqiu.com/6218450268/133577046)
查资料得出氢原子半径25皮米,直径 50E-12,也就是 5E-11米
目前可观测宇宙半径 460亿光年,周常 5.5264E27 米
也即是说,以氢原子来测量可观测宇宙尺度的一个完美大圆,算出来的圆周率,能够精确到 大约小数点后38位。你还能有更大的圆、更精细的尺子么?即使有,又能多几个有效位呢?
直接测算,有大量绝对无法避免的误差,就像我上面说的,圆的大小,误差的引入(直径的选择、铁丝没掰直、铁丝本身直径),测量的精度,一系列问题,根本不可能获得一个比较好的精度。
事实上,祖冲之这些古人,早都已经放弃直接测量的方式来算圆周率,而是采用割圆术,纯粹的数学计算。而祖冲之靠这个方法,计算到圆周率小数点后七位。直接测量的话,你需要一个直径1km级别的完美圆,然后测量这个圆的时候要保证误差在1毫米以内才能测出这么精细的值。
割圆术采用的是几何方法,理论基础是,通过计算圆内接-外切正多边形的边长,以此逼近圆的周长。通过数学计算而不是测量来得到圆的周长。如果你的孩子已经了解勾股定理,以及圆的一些基本性质,可以让他了解割圆术,其实主要就是计算量(不过涉及到大量开方、平方计算,必须计算器辅助,而计算器在开方平方再一次引入误差)。
而现代用解析几何、微积分对圆周率给出了新的迭代计算公式,加上计算机编程,可以轻松计算出来。
可以说: 以1+1=2为基础的代数,可以推导出圆周率绝对不是两个整数的比值,一定是无理数。 (证明涉及大学知识)。
古代采用割圆术计算,最简单的迭代公式:
计算:
(正十二边形)
(24)
(48)
(96)
根据九十六边形计算得出的圆周率
而用无穷奇数,来计算圆周率
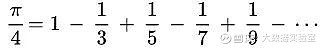
计算100万项(C语言编程计算)后可以得出
另一个公式:
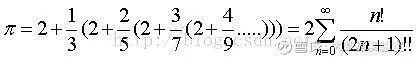
对应的程序:
#include
long a=10000,b,c=2800,d,e,f[2801],g;
main()
{
for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)
for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);
}
可以轻松计算800位的圆周率,并且通过调整参数,可以轻松计算更多位。
而目前的记录,采用

这种类似的公式,已经把圆周率计算到了1万亿位。
试问,如此高的精度,又是什么样的尺子能量出来的呢?
以上涉及的公式,需要用到不同级别的知识来推导。其中割圆术公式,只需要初中知识,学过勾股定理就能计算,后面的无穷级数公式,需要到大学才能尝试。可以先告诉你娃这些公式,告诉他,用这个公式就能算出来更精确的圆周率,至于为什么,需要继续学习,就能知道。而不是现在一头愣的非要测量。
就像一个很简单但是很巧妙的题:今天周二,2^2019天之后是周几?难道你要死命去乘么?实际上了解规律找到方法,口算就能算出来。(小学知识)
来源:数学职业家


