时间:
星期一 第3节–第4节(10:00 AM – 11:40AM)、星期四(双周)) 第1节–第2节(8:00AM – 9:40AM)
地点:
下院114 (1-16周)
课本:
上海交通大学数学系,线性代数(第三版),科学出版社,2014
MOOC(慕课)地址
平时:20%,大作业: 10% 期末:70%
就线性代数中有意思的定理,例题或相关应用写一份学习报告. 报告长度控制在2面A4纸以内.
12月22日23:59前
请将大作业发至邮箱: [email protected]
邮件标题格式: 2019线性代数大作业-xxxxxxxxx-姓名 (xxxxxxxxx为学号)
课件(ppt)
行列式的定义
行列式的性质
行列式按行列展开
拉普拉斯定理
行列式的计算
矩阵的概念和运算
矩阵的分块
初等变换-1
作业1, 9月23日交: p41 习题一: 1.2, 1.3, 1.5, 3, 4, 7
作业2, 9月30日交: 习题一: 8.1, 11.1, 12.1, 12.4, 12.5, 12.6, 13.1, 13.3, 19.2, 20.4
作业3, 10月14日交: 习题一: 14.1, 14.3, 14.5, 15, 16, 17
作业4, 10月21日交: 习题二: 6, 7.1, 7.3, 8, 9, 10, 13, 15, 17, 27, 32, 33
作业5, 10月28日交: 习题二: 21.2, 21.7,22.1,22.3, 22.4, 26, 28
作业6, 11月11日交: 习题二: 47, 48, 49, 51.1, 51.3, 51.5, 52, 53, 54 习题三: 1, 3, 4, 6.1, 6.2, 7.1, 8 思考题(不用交) 9
作业7, 11月18日交: 习题三: 17, 19.2, 20.2, 22, 23, 24.1,24.3, 24.5, 25, 26, 27.1, 27.2, 28.2, 33, 35
作业8, 12月02日交: 习题四: 3.1, 3.2, 3.3, 4.1, 4.3, 4.5, 6.1, 6.2, 6.3, 7, 9, 12, 13.2, 17
作业9, 12月09日交: 习题四: 18, 19, 22, 23.1, 24 思考题: 25
作业10, 12月16日交: 习题五: 1.3, 1.4, 1.6, 2, 6, 7, 11, 12, 17.2, 20, 22
[S] Serre, A course in Arithmetic
[SL]
Serre, Local Fields
[SD] Swinnerton-Dyer, A Brief Guide to Algebraic Number Theory
[N] Neukirch, Algebraic Number Theory
Weil, Basic Number Theory
[AM] Atiyah and MacDonald, Introduction to Commutative Algebra
[CF] Algebraic Number Theory, Proceedings of an Instructional Conference Organized by the London Mathematical Society
[M]
J.S. Milne, Class Field Theory
[A]
Michael Artin on noncommutative ring theory
[FD]
Farb and Dennis, Noncommutative Algebra, Chapter 4: The Brauer Group
第二章, 问题 4,12,习题 2.2
第三章, 问题 3,习题 3.4
期末报告备选问题:
Gamma函数与Sin函数的乘积公式.
Erica Chan, The Sine Product Formula and the Gamma Function
复数域上的椭圆曲线 J.S. Milne, Elliptic Curves; Silverman, The Arithmetic of Elliptic Curves,
An online lecture note
Galois理论的回顾, Trace和Norm [K] 附录, [N] Section I.2
分圆域(Galois群,整数环,理想的分解等) [K] 相关章节, [N] Section I.10 [SD] Section 13
整闭整环及其扩张. [AM] Chapter 5, [N] Section I.2
局部化,局部环. [N] Section I.11
Noether环,Artin环及例子 [AM] Chapter 6-8
Dedekind环的定义,基本性质及例子. [N] Section I.3 [AM] Chapter 9 [CF] Section I.2
共轭差积与判别式 (Difference and Discriminant) [N] III.2 [K] 6.3(b)
理想及分式理想的分解 [N] Section I.3 [AM] Chapter 4, Chapter 9 [CF] Section I.2
逆向极限, pro-finite group及在Galois理论中的应用. [CF] Section V.1
完备局部域, Hensel引理及p-aidc域的乘法群结构. [S] Chapter 2 [N] Proposition II.5.7
不变测度及命题6.81,6.82的证明. [K] 6.4(g)节 [SD] 附录
Pontrjagin对偶, 例子,及命题6.79的证明. [K] 6.4(h)节.
中心单代数及Brauer群的定义 [A] [M] Chapter 4 [SL] X.5, [FD]
Brauer群的例子(有限域,局部域及inv映射) [A] [M] Chapter 4, [SL] X.5 XII, [FD]
关于素数分布的定理 [K] 第七章相关部分
L-函数的函数方程 [K] 第七章相关部分
类域论在函数域情况下的结果. [K] 课本相关内容 [N] Section I.14
期末报告 地点:数学楼1106,2017年12月17日
题目及时间:
09:00 — 09:30
Gamma函数与Sin函数的乘积公式
09:30 — 10:00
复数域上的椭圆曲线 J.S. Milne, Elliptic Curves; Silverman, The Arithmetic of Elliptic Curves
10:00 — 10:30
Galois理论的回顾, Trace和Norm [K] 附录, [N] Section I.2
10:30 — 11:00
分圆域(Galois群,整数环,理想的分解等) [K] 相关章节, [N] Section I.10 [SD] Section 13
11:00 — 11:30
整闭整环及其扩张. [AM] Chapter 5, [N] Section I.2
11:30 — 12:00
Noether环,Artin环及例子 [AM] Chapter 6-8
13:00 — 13:30
Dedekind环的定义,基本性质及例子. [N] Section I.3 [AM] Chapter 9 [CF] Section I.2
13:30 — 14:00
共轭差积与判别式 (Difference and Discriminant) [N] III.2 [K] 6.3(b)
14:00 — 14:30
理想及分式理想的分解 [N] Section I.3 [AM] Chapter 4, Chapter 9 [CF] Section I.2
14:30 — 15:00
逆向极限, pro-finite group及在Galois理论中的应用. [CF] Section V.1
15:00 — 15:30
完备局部域, Hensel引理及p-aidc域的乘法群结构. [S] Chapter 2 [N] Proposition II.5.7
15:30 — 16:00
不变测度及命题6.81,6.82的证明. [K] 6.4(g)节 [SD] 附录
16:00 — 16:30
Pontrjagin对偶, 例子,及命题6.79的证明. [K] 6.4(h)节.
16:30 — 17:00
中心单代数及Brauer群的定义 [A] [M] Chapter 4 [SL] X.5, [FD]
17:00 — 17:30
Brauer群的例子(有限域,局部域及inv映射) [A] [M] Chapter 4 [SL] X.5 XII, [FD]
17:30 — 18:00
关于素数分布的定理 [K] 第七章相关部分
不变子空间
 存在基使得在这组基下线性映射成分块上(下)三角形;
空间的分解成不变子空间的直和
存在基使得在这组基下线性映射成分块上(下)三角形;
空间的分解成不变子空间的直和
 存在基使得在这组基下线性映射成分块对角矩阵;
特征值, 特征向量, 矩阵/线性变换可对角化
存在基使得在这组基下线性映射成分块对角矩阵;
特征值, 特征向量, 矩阵/线性变换可对角化
 存在一组由特征向量组成的基
任意有限维空间上的线性变换有若当标准型, (幂零)若当块
存在一组由特征向量组成的基
任意有限维空间上的线性变换有若当标准型, (幂零)若当块
 循环子空间, 幂零变换的若当标准型, 广义特征子空间
矩阵(线性变换的)函数(多项式或幂级数): 对多项式
循环子空间, 幂零变换的若当标准型, 广义特征子空间
矩阵(线性变换的)函数(多项式或幂级数): 对多项式
 可以定义
可以定义
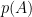 , 可以定义矩阵的指数
, 可以定义矩阵的指数
 , (事实上如果矩阵可对角化, 可以对任意连续函数可以定义矩阵函数
Functional calculus
…)
用若当标准型计算
, (事实上如果矩阵可对角化, 可以对任意连续函数可以定义矩阵函数
Functional calculus
…)
用若当标准型计算
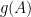 带有附加配对(paring)结构的线性空间, (Paring: 线性空间上的对称、共轭对称或反对称的非退化双线性函数)
(伪)内积,酉内积,辛内积
带有附加配对(paring)结构的线性空间, (Paring: 线性空间上的对称、共轭对称或反对称的非退化双线性函数)
(伪)内积,酉内积,辛内积
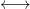 欧氏空间, (伪)欧氏空间,酉空间,辛空间
(酉)内积空间中的Cauchy-Schwarz不等式, 三角不等式
任取基, 得度量矩阵:
欧氏空间, (伪)欧氏空间,酉空间,辛空间
(酉)内积空间中的Cauchy-Schwarz不等式, 三角不等式
任取基, 得度量矩阵:
内积, (伪)内积, 酉内积, 辛内积 分别对应 正定对称矩阵, 可逆的对称矩阵, 正定的共轭对称矩阵, 反对称矩阵
换基
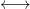 矩阵的合同(congruence)变换 (即
矩阵的合同(congruence)变换 (即
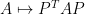 或(在酉空间中)
或(在酉空间中)
 )
存在特别的基: 标准正交基(对欧氏空间, 酉空间), 辛空间(辛基), 对应的度量矩阵特别简单
)
存在特别的基: 标准正交基(对欧氏空间, 酉空间), 辛空间(辛基), 对应的度量矩阵特别简单
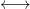 矩阵
标准正交基的构造: Gram–Schmidt方法
矩阵
标准正交基的构造: Gram–Schmidt方法
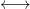 (可逆)矩阵的QR分解(即分解为正交矩阵和上(或下)三角矩阵的乘积)
保持结构的线性变换/矩阵(这些变换组成一个群): 正交变换/矩阵, 酉变换/矩阵, 辛变换, (伪内积空间上可以定义类似的变换)
非退化的配对结构
(可逆)矩阵的QR分解(即分解为正交矩阵和上(或下)三角矩阵的乘积)
保持结构的线性变换/矩阵(这些变换组成一个群): 正交变换/矩阵, 酉变换/矩阵, 辛变换, (伪内积空间上可以定义类似的变换)
非退化的配对结构
 Adjoint/Transpose的概念
谱理论: 对称变换/矩阵(或正规变换)可以在某个标准正交基/用某个正交矩阵(或酉矩阵) 对角化;
Adjoint/Transpose的概念
谱理论: 对称变换/矩阵(或正规变换)可以在某个标准正交基/用某个正交矩阵(或酉矩阵) 对角化;
半正定矩阵
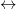 对角线上非负数 (所以这样的矩阵可以求”开方”),
对角线上非负数 (所以这样的矩阵可以求”开方”),
Hermit矩阵
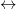 对角线上实数,
对角线上实数,
酉矩阵
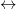 对角线上是单位根
对角线上是单位根
正交矩阵的标准形(分块对角矩阵, 每一块要么是
 要么是个旋转.
其他的常见分解: 极分解(Poler decomposition), (SVD分解…)
(伪内积空间与内积空间的异同, 不同, 如存在长度为零的非零向量.)
要么是个旋转.
其他的常见分解: 极分解(Poler decomposition), (SVD分解…)
(伪内积空间与内积空间的异同, 不同, 如存在长度为零的非零向量.)
多项式环, 整数环, (一般的环的概念, 交换环, 零因子, 整环等概念…)
(多项式)环的理想的概念, 主理想的概念, 一元多项式环与整数环是主理想整环, 多元多项式环不是
最大公因子/互素, 最小公倍数的概念及其与对应的理想的关系; 环中的单位(unit即可逆元)的概念, 不可约元/素元/(素理想)的概念, 唯一分解整环/唯一分解定理, 整数环是唯一分解整环(算术基本定理), (一元或多元)多项式环是唯一分解整环.
中国剩余定理(和它的环论描述)
多项式环中的因式分解:
在复数域上分解为一次多项式的乘积(代数基本定理), 重根的概念, 及重根重数的判定法则
在实数域上, 分解为一次或二次多项式的乘积.
有理数域/整数环上, 分解为本原多项式的乘积, (一类本原多项式不可约的判别法: Eisenstein判别法)
整数环, 整数环的商环(即同余类组成的环), Euler函数(另一种看法:
 中可逆元的个数)和它的计算公式, (积性函数Multiplicative function的概念), Euler定理/Fermat小定理
(用一元多项式环进一步理解线性变换的不变子空间/Jordan标准型的理论.)
(多元多项式环这的”首项”的概念, 初等对称多项式, 根与系数关系, 对称多项式基本定理, 判别式, 指数和/牛顿关于初等对称多项式与指数和之间关系的等式)
中可逆元的个数)和它的计算公式, (积性函数Multiplicative function的概念), Euler定理/Fermat小定理
(用一元多项式环进一步理解线性变换的不变子空间/Jordan标准型的理论.)
(多元多项式环这的”首项”的概念, 初等对称多项式, 根与系数关系, 对称多项式基本定理, 判别式, 指数和/牛顿关于初等对称多项式与指数和之间关系的等式)
仿射空间, 度量空间, 射影空间的概念;
选取仿射标架,正交标架(射影坐标系)
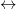
将空间等同于
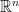
(或

)
保持结构的变换: 仿射变换, 保距变换, (射影变换);
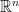
(或

)上这些变换的矩阵表达形式
换标架
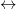
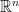
上的仿射/保距变换.
(Klein和Erlangen纲领:几何=研究变换下的不变量)
方程和图形: 一般方程, 参数方程
二/三维空间中的例子: (三维空间中的特殊工具:外积(叉积,cross product))
直线, 平面的的方程
二次曲线和二次曲面:
典型的二次曲线和二次曲面的方程和图形
二次曲线、曲面的等距分类/仿射分类/射影分类
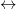
本质上是对称矩阵在不同变换下的等价类.
二次曲面与平面的截线
典型的非平凡的直纹面: 单叶双曲面, 双曲抛物面
(用仿射变换/射影变换证明平面几何中的问题…)