|
|
完美的莴苣 · valgrind检测内存问题的原理-电子发烧友网· 3 月前 · |
|
|
千杯不醉的回锅肉 · 网络热门ChatGPT量化交易研究报告盘点( ...· 8 月前 · |
|
|
温文尔雅的作业本 · 记一次爬虫逆向攻防的详细过程-腾讯云开发者社 ...· 11 月前 · |
|
|
坚韧的南瓜 · 硕博人才在线|权威的人才招聘平台|博士招聘| ...· 1 年前 · |
|
|
很酷的橡皮擦 · 电影《爱很美味》4月15日上映,“美味三姐妹 ...· 1 年前 · |
布尔运算是逻辑门的基础,逻辑门和布尔代数的定律构成了数字电路的基础。本文的目的是对布尔表达式进行化简,化简的目的是在实际电路中使用更少的逻辑门。一个逻辑电路有三种表达方式,分别是布尔表达式,真值表,以及卡诺图。真值表最直观,卡诺图适合化简,布尔表达式适合运算。布尔表达式,真值表,卡诺图相互之间可以转换。
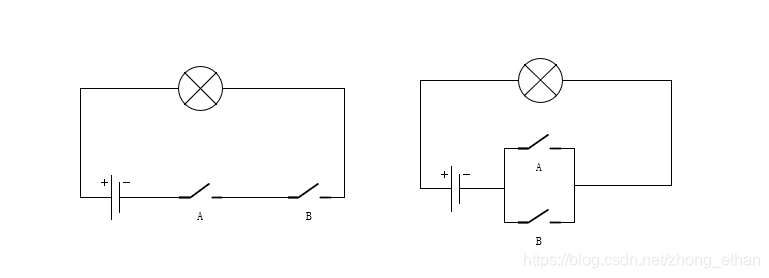
先看一个小例子:图左为开关串联电路,只有在开关A和B都同时闭合的情况下,小灯泡才会亮;图右为开关并联电路,当开关A和开关B至少有一个闭合时,小灯泡就会亮,这种逻辑关系成为布尔运算。布尔运算是一切逻辑的本质。
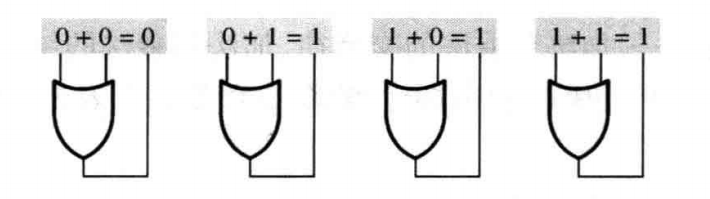
布尔加法
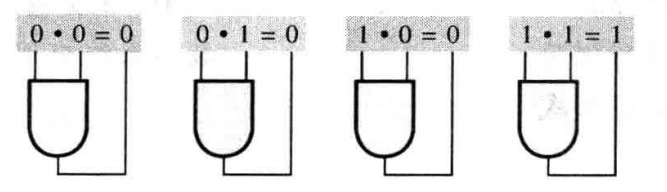
布尔乘法
布尔非运算
1
ˉ
=
0
布尔代数定律
交换律 A +B = B + A AB=BA
结合律 (A+ B)+C=A+(B+C) (AB)C=A(BC)
分配律 A(B+C)=AB+BC
好不夸张的说,掌握了布尔运算与布尔代数定律就掌握了数字电路。因为接下来所有的逻辑化简必须遵从以上两点。
布尔代数常用基本法则
( A + B ) ( A + C ) = A A + A C + A B + B C = A + A C + A B + B C = A + A B + B C = A + B C
狄摩根第一定理: A + B = A + B + C . C ˉ = ( A + B + C ) ( A + B + C ˉ ) 。通过这种方法,可以把所有的非标准和项转成标准和项。
最小项之和与最大项之积互相转换 非常简单,只需要狄摩根定理就可以。
**最小项之和和最大项之积意义?**可以快速的得到布尔表达式的真值表和进行布尔表达式化简
布尔表达式和真值表
最小项之和转换成真值表
对于域中有
(
A
+
B
+
C
)
(
A
+
B
ˉ
+
C
)
(
A
+
B
ˉ
+
C
ˉ
)
(
A
ˉ
+
B
+
C
ˉ
)
(
A
ˉ
+
B
ˉ
+
C
)
。在ABC分别为000,010,011,101和110时,表达式的结果为0。因此得到如下真值表:
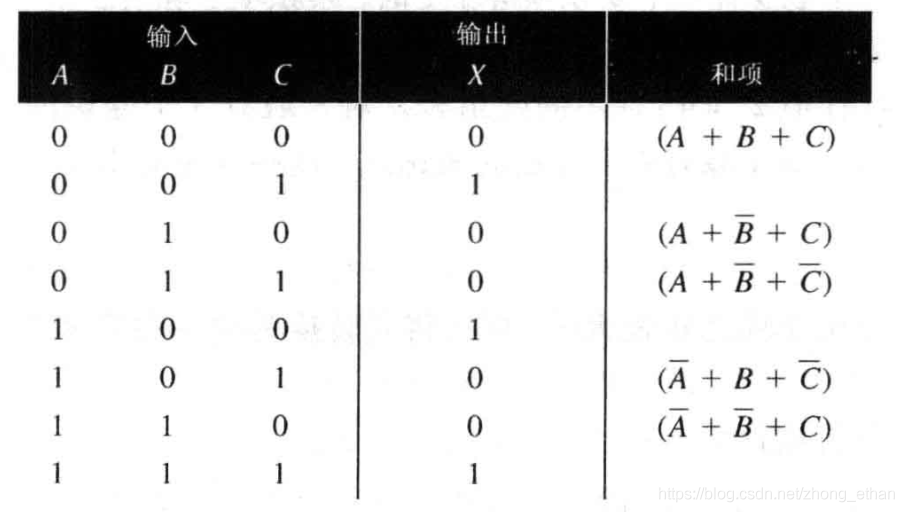
真值表转换成最小项之和或最大项之积
非常简单,只要将上面两个过程反过来就可以。
卡诺图的作用是化简布尔表达式,只要出现形如 A B ( C + C ˉ ) 。两个乘积项在卡诺图中处在相邻的两个小方块中。
最小项之和的卡诺图映射
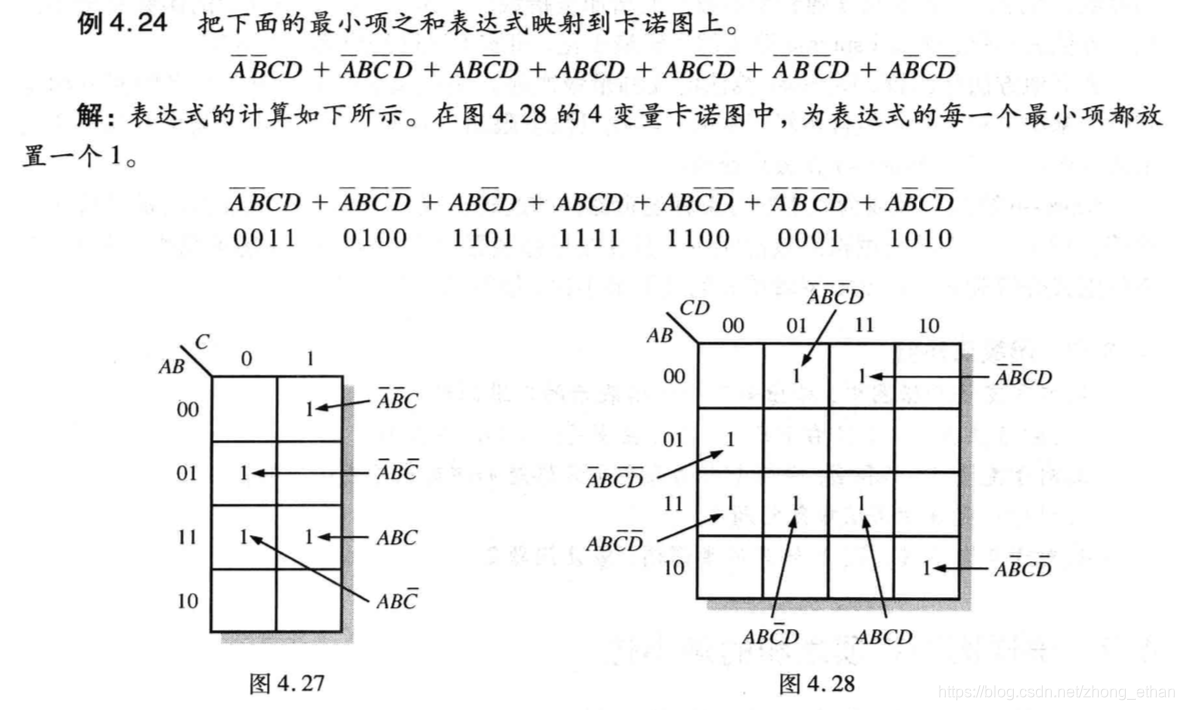 对于一些无效的组合,即在实际情况中并不会发生的变量组合,在卡诺图上可以当成无关项来处理。无关项可以是0也可以是1,用X来表示。
对于一些无效的组合,即在实际情况中并不会发生的变量组合,在卡诺图上可以当成无关项来处理。无关项可以是0也可以是1,用X来表示。
卡诺图化简
化简的基本目的是:圈尽可能的大, 组尽可能的小
1、一个小组只能含
布尔运算是逻辑门的基础,逻辑门和布尔代数的定律构成了数字电路的基础。本文的目的是对布尔表达式进行化简,化简的目的是在实际电路中使用更少的逻辑门。一个逻辑电路有三种表达方式,分别是布尔表达式,真值表,以及卡诺图。真值表最直观,卡诺图适合化简,布尔表达式适合运算。布尔表达式,真值表,卡诺图相互之间可以转换。
注意:这是此软件的初始计划,以后可能会添加许多其他功能。
创建
逻辑
电路-用户可以在许多标准
逻辑
门之间进行选择,也可以在自己创建的电路之间进行选择并将其连接到主面板中。
模拟-可以测试(模拟)用户制作的
数字电路
。 用户将从电路的所有部分获得有关
逻辑
状态的信息。
黑匣子功能-此功能允许用户创建自己的“标准”电路,以后可将其用作单个元素。
逻辑
转换:
将
逻辑
功能转换为
逻辑
电路。
将
逻辑
电路转换成
逻辑
功能。
函数
最小
化-返回输入函数的
最小
形式。 使用以下方法可以实现功能
最小
化:McCluskey方法,Quine方法,Veitch图(某些其他方法也可能在以后添加)。 用户将能够逐步检查
最小
化过程的解决方案。
NAND / NOR调整-以NAND / NOR表示形式返回