,将曲率积大于阈值的定义为关键点。
但MSCP未能解决差分法求曲率对噪声的鲁棒性问题以及对轨迹中曲率较小的弱关键点求曲率积会导致曲率下降、关键点遗漏。
为解决上述问题,对传统的多尺度曲率积算法做出两点改进。1) 采用第一类切比雪夫多项式拟合当前及邻域内的点集,使用参数方程的曲率公式代替传统的差分法求曲率。2) 对曲率较小的弱关键点求不同尺度的曲率和以增强曲率较小处的关键点。实验结果证明本算法的曲率对波动较大的噪声具有一定的鲁棒性,对曲率较小的弱关键点也有较好的提取效果。
2.1. 基于切比雪夫多项式的曲率估计
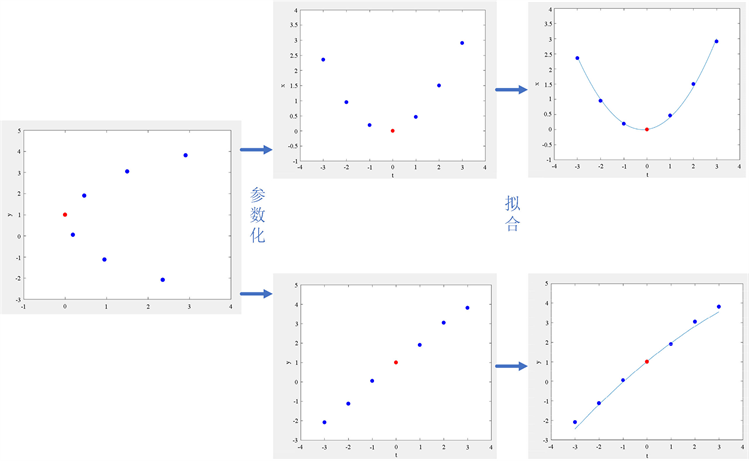
Figure 1
. Fitting process of Chebyshev polynomial
图1
. 切比雪夫多项式的拟合过程
为解决差分法求曲率容易受噪声影响的问题,采用切比雪夫多项式拟合当前及邻域内的点集,通过参数方程的曲率公式求得当前点的曲率。第一类切比雪夫多项式对扰动不敏感、能有效地降低龙格现象等优点 [7],其拟合过程如
图1
所示。
设当前轨迹点为
(4)
分别使用差分法和切比雪夫多项式求星型轨迹的曲率,由
图2
可知,采用切比雪夫多项式曲线拟合求曲率具有对噪声具有更好的鲁棒性。
2.2. 弱关键点增强
MSCP算法对不同尺度下的曲率求乘积可以有效地增强关键点处的曲率,降低噪声点处的曲率,但是MSCP算法对曲率较小的弱关键点(曲率值小于1)却会产生抑制效果,从而导致关键点的缺失,因此引入多尺度曲率和的概念,在不同的尺度下,对局部曲率极大值处求和,对局部曲率非极大值处求积,流程如
图3
所示。
星型轨迹弱关键点增强前后曲率图及提取效果如
图4
所示。
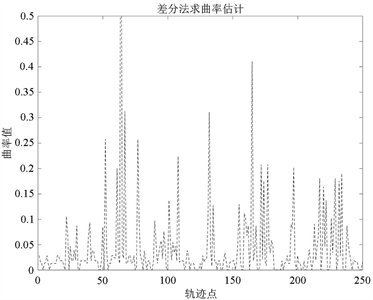 (a) 差分法曲率估计
(a) 差分法曲率估计
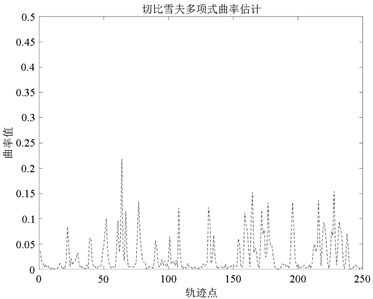 (b) 切比雪夫多项式曲率估计
(b) 切比雪夫多项式曲率估计
Figure 2
. Comparison of curvature estimation by difference method and Chebyshev polynomial curvature estimation
图2
. 差分法曲率估计与切比雪夫多项式曲率估计效果对比
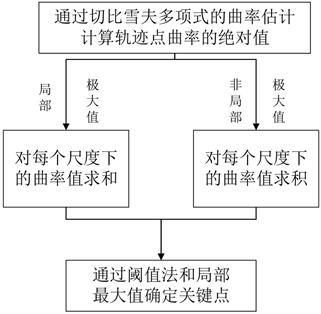
Figure 3
. Weak key point enhancement process
图3
. 弱关键点增强流程
3. 公共关键点识别
由于操作者在示教过程的抖动、不熟练等因素,单次示教往往不能精确的拟合出示教轨迹,本文采用对同一工作重复示教,通过多条轨迹产生精确的示教轨迹,但不同的示教轨迹的关键点空间位置、数量以及轨迹点的时间戳都不相同。隐马尔可夫模型(HMM)可以对时间序列建模,对复杂的轨迹也具有较高的识别精度 [8]。但HMM模型在同一状态的驻留时间呈指数级下降,这与实际情况不符。而HSMM是隐马尔可夫模型(HMM)的一种扩展形式,与HMM最大的不同是HSMM加入驻留时间的概念。因此本文采用连续隐半马尔可夫模型(CHSMM)模型对连续的轨迹点建模,提取所有轨迹中特征一致的公共关键点 [8]。
CHSMM的拓扑图如
图5
所示,对于一组观测变量
是其对应概率最大的隐状态。1、2、3对应的是宏观状态,即隐状态没有发生转移。
图4
. 关键点增强前后MSCP算法关键点提取效果对比
图5
. CHSMM的拓扑图
3.1. CHSMM的模型初始化
CHSMM模型参数可以表示为
是初始状态概率,
为状态驻留概率,使用一个单元高斯分布函数描述模型在每个宏观状态驻留时间的概率分布。CHSMM模型的隐状态、观测状态的数量与关键点的个数对应。因此将隐状态及观测状态的数量设为所有演示中关键点数量的最大值 [9]。对所有的示教轨迹使中Baum-Welch算法进行训练,得到CHSMM的参数
。
3.2. 公共关键点识别
获得模型参数后,对于每条轨迹的观察序列
使用Viterbi算法获取对应隐状态序列 [10]。由于关键点是运动特征发生变化的点,因此对应的隐状态也会发生改变。为验证关键点是否为公共关键点,本文提出转移状态
的概念,以当前关键点
为中心设置邻域为5的窗口
,对应的关键点为公共关键点。
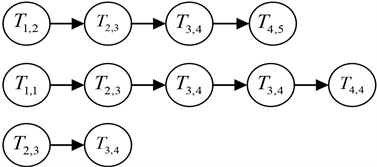
Figure 7
. Key point transition states generated by three demonstrations
图7
. 三次演示产生的关键点转移状态
4. 轨迹生成
以各公共关键点簇的中心点作为示教轨迹的分割点,形状复杂的轨迹被分割为多条结构简单的子轨迹。由于三次B样条曲线具有灵活的造型性能,曲线连接光滑,计算简便等优点,因此使用三次准均匀B样条曲线对各子轨迹进行分段拟合,生成最终的示教轨迹 [11]。
B样条曲线的定义为:
与轨迹的首尾点重合 [12],因此需要基于最小二乘法求得中间两个控制点的位置。
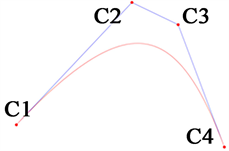 —拟合曲线;—控制多边形
—拟合曲线;—控制多边形
Figure 8
. Cubic quasi-uniform B-spline
图8
. 三次准均匀B样条
首先使用弦长参数化来估算每个轨迹点的参数
,轨迹点与拟合曲线上对应点的距离误差公式为:
,然后根据控制点生成示教轨迹 [12]。
5. 对比验证
为了对示教算法进行评估,搭建如
图9
(a)所示的实验装置。操作员操作示教笔完成半圆柱体的涂漆工艺的轨迹示教,目标轨迹如
图9
(b)所示。kinect深度相机及视觉系统跟踪示教笔的位置及姿态,示教完成后通过ROS系统驱动六轴机械臂画出示教轨迹以完成轨迹复现 [13]。
图10
实验零件及目标轨迹本次实验产生五组有效轨迹,分别使用传统的多尺度曲率积算法以及改进后的多尺度曲率积算法求取当前轨迹的曲率积,通过设置阈值获取关键点,结果如
图10
所示,改进的MSCP算法提取关键点的数量和位置都更为精确。
为了获取所有演示的公共关键点,我们使用CHSMM对轨迹进行训练,隐状态数量设置为12,通过Viterbi算法计算每个关键点及其领域的隐状态和转移状态,根据转移状态的出现的频率获取公共关键点。
 (a) 轨迹获取
(a) 轨迹获取
 (b) 目标轨迹
(b) 目标轨迹
Figure 9
. Teaching trajectory acquisition and target trajectory
图9
. 示教轨迹获取与目标轨迹
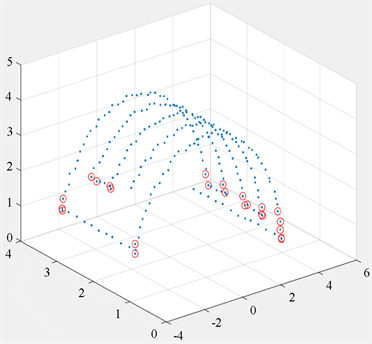
(a) MSCP算法改进前
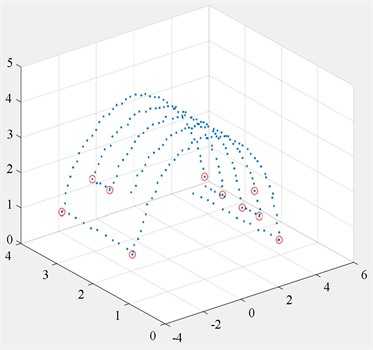
(b) MSCP算法改进后
Figure 10
. Comparison of key point extraction results before and after the improvement of the multi-scale curvature algorithm
图10
. 多尺度曲率算法改进前后的关键点提取效果对比
本文采用的CHSMM提取公共关键点与传统方法使用CHMM的提取效果对比如
图11
所示,不同颜色的轨迹点代表不同示教轨迹。由
图11
可知CHSMM提取的公共关键点更集中,无
图11
(b)中冗余的、离散的公共关键点,公共关键点提取效果更佳。
将公共关键点簇的中心点作为轨迹的分割点以及拟合曲线的起点与终点。利用中心点将复杂轨迹分割为形状简单的子轨迹,对各段子轨迹采用基于最小二乘法的B样条曲线拟合,得到的示教轨迹如
图12
(a)所示。
图12
(b)为使用最小二乘B样条拟合得到的轨迹。相较于传统方法中仅使用最小二乘B样条拟合整个轨迹,本文拟合轨迹产生的形变较小,与目标轨迹更具一致性。
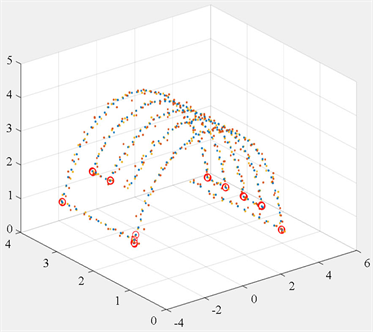 (a) CHSMM提取的公共关键点
(a) CHSMM提取的公共关键点
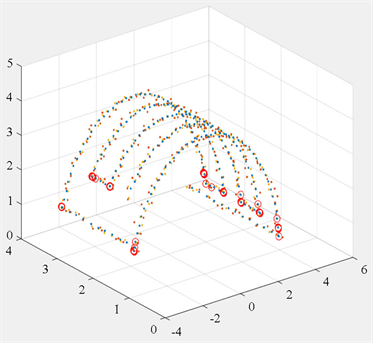 (b) HMM提取的公共关键点
(b) HMM提取的公共关键点
Figure 11
. Comparison of common key point extraction effects between CHSMM and CHMM
图11
. CHSMM与CHMM公共关键点提取效果对比
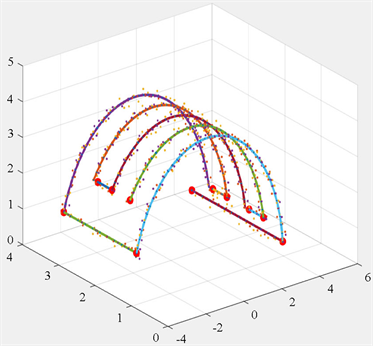 (a) 本文拟合生成的轨迹
(a) 本文拟合生成的轨迹
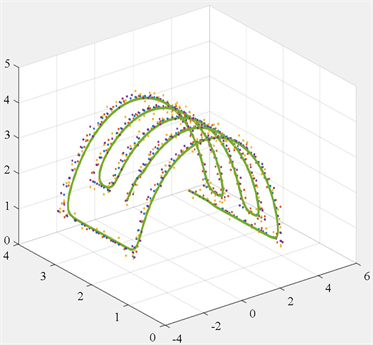 (b) 使用最小二乘B样条拟合的轨迹
(b) 使用最小二乘B样条拟合的轨迹
Figure 12
. Comparison of the generated trajectories
图12
. 生成的轨迹对比
6. 结论
本文提出一种通过演示示教生成复杂轨迹的示教算法,它由关键点提取、公共关键点识别、轨迹拟合几个部分组成。相较于传统的轨迹生成办法,如最小二乘曲线拟合示教轨迹,本文利用多条示教轨迹信息,以各个公共关键点簇的中心点作为轨迹分割点,将形状复杂、不易拟合的多条轨迹分割成多条结构简单的子轨迹,使用三次B样条对子轨迹分段拟合。生成的轨迹与目标轨迹具有较高的一致性。
为了提高轨迹分割的效果,本文对MSCP算法进行改进,以切比雪夫多项式的曲率估计代替传统的差分法求曲率,增强了算法的噪声鲁棒性。使用弱角点增强算法有效解决了MSCP小曲率关键点遗漏的问题。通过CHSMM对轨迹建模,提取所有示教轨迹的公共关键点,相较于传统的HMM模型,CHSMM有效解决了HMM同一状态驻留时间呈指数级下降的问题,具有更好的建模精度,提取的公共关键点位置精度更高,冗余公共关键点数量更少。
文章引用
花傲阳. 基于连续隐半马尔可夫模型的复杂轨迹演示示教算法研究
Research on Teaching Algorithm of Complex Trajectory Demonstration Based on Continuous Hidden Semi-Markov Model[J]. 建模与仿真, 2022, 11(04): 1031-1041.
https://doi.org/10.12677/MOS.2022.114095
参考文献
-
1. Song, C.W., Liu, G.F., Zhang, X.H., et al. (2020) Complex Motion Learning Based on Unsupervised Trajectory Segmentation and Movement Primitives. ISA Transactions, 97, 325-335.
https://doi.org/10.1016/j.isatra.2019.08.007
-
2. Daniel, M., Carina, V., Marc, S., et al. (2020) One-Shot Kinesthetic Programming by Demonstration for Soft Collaborative Robots. Mechatronics, 70, Article No. 102418.
https://doi.org/10.1016/j.mechatronics.2020.102418
-
3. Wang, Q.Y., Jiao, W.H., Yu, R., et al. (2019) Modeling of Human Welders’ Operations in Virtual Reality Human-Robot Interaction. IEEE Robotics and Robotics and Automation Letters, 4, 2958-2964.
https://doi.org/10.1109/LRA.2019.2921928
-
4. 张宏达. 基于球杆示教笔的机器人轨迹演示编程系统研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2020.
-
5. Vakanski, A., Mantegh, I., Irish, A., et al. (2012) Trajectory Learning for Robot Programming by Demonstration Using Hidden Markov Model and Dynamic Time Warping. IEEE Transactions Systems, Man, and Cybernetics. 42, 1039-1052.
https://doi.org/10.1109/TSMCB.2012.2185694
-
6. 张世征. 几种轮廓曲率估计角点检测算法研究[D]: [博士学位论文]. 重庆: 重庆大学, 2016.
-
7. 洪庆飞. 图像轮廓的B样条拟合和优化研究[D]: [硕士学位论文]. 杭州: 杭州电子科技大学, 2021.
-
8. Javier, G., Yu, W. and Li, X.O. (2016) Robot Trajectory Generation Using Modified Hidden Markov Model and Lloyd’s Algorithm in Joint Space. Engineering Applications of Artificial Intelligence, 53, 32-40.
https://doi.org/10.1016/j.engappai.2016.03.006
-
9. 杨柳. 基于隐半马尔可夫模型的液压泵剩余使用寿命预测[D]: [硕士学位论文]. 西安: 西安电子科技大学, 2018.
-
10. Fabien, D., David, B., Germain, F., et al. (2016) Unsupervised Trajectory Segmentation for Surgical Gesture Recognition in Robotic Training. IEEE Transactions on Biomedical Engineering, 63, 1280-1291.
https://doi.org/10.1109/TBME.2015.2493100
-
11. 沈靖皓. 基于手势引导的工业机器人示教技术研究及应用[D]: [硕士学位论文]. 杭州: 浙江大学, 2017.
-
12. 李鹤喜. 基于视觉反馈的焊接机器人自主示教关键技术研究[D]: [博士学位论文]. 广州: 华南理工大学, 2010.
-
13. 罗华亮. 基于双目视觉及示教笔的三维示教轨迹获取研究及实现[D]: [硕士学位论文]. 武汉: 武汉理工大学, 2020.
●投稿须知
●最新文章

 (a) 差分法曲率估计
(a) 差分法曲率估计
 (b) 切比雪夫多项式曲率估计
(b) 切比雪夫多项式曲率估计

 (a) 弱关键点增强前
(a) 弱关键点增强前
 (b) 弱关键点增强后
(b) 弱关键点增强后
 (c) 增强前关键点
(c) 增强前关键点
 (d) 增强后关键点
(d) 增强后关键点


 —拟合曲线;—控制多边形
—拟合曲线;—控制多边形
 (a) 轨迹获取
(a) 轨迹获取
 (b) 目标轨迹
(b) 目标轨迹
 (a) MSCP算法改进前
(a) MSCP算法改进前
 (b) MSCP算法改进后
(b) MSCP算法改进后
 (a) CHSMM提取的公共关键点
(a) CHSMM提取的公共关键点
 (b) HMM提取的公共关键点
(b) HMM提取的公共关键点
 (a) 本文拟合生成的轨迹
(a) 本文拟合生成的轨迹
 (b) 使用最小二乘B样条拟合的轨迹
(b) 使用最小二乘B样条拟合的轨迹