✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:
Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法
神经网络预测
雷达通信
无线传感器
电力系统
信号处理
图像处理
路径规划
元胞自动机
无人机
⛄ 内容介绍
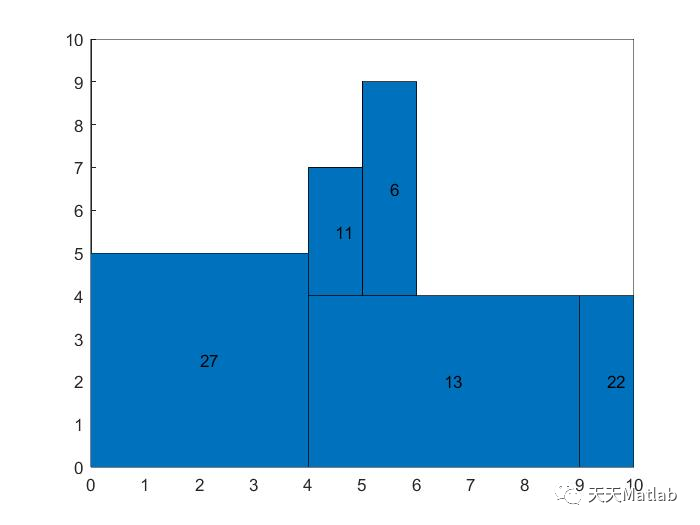
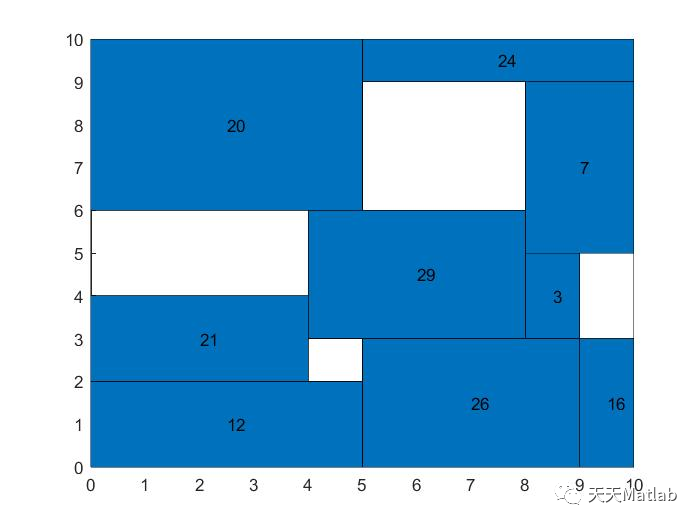
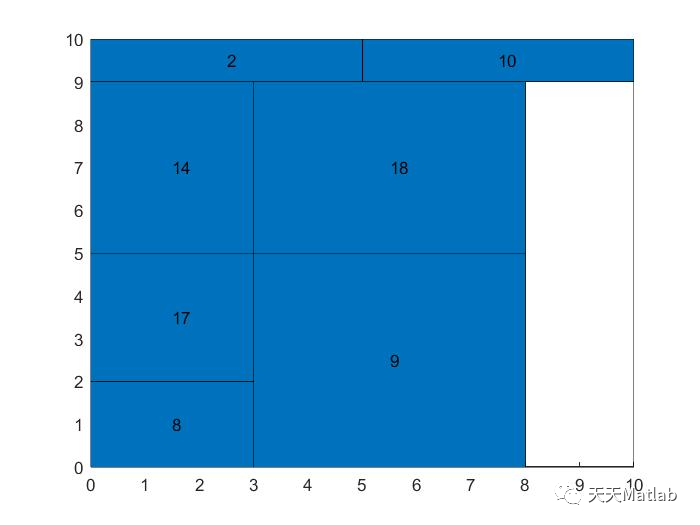
二维装箱问题顾名思义就是将若干个矩形物品装进矩形箱子中,并且在装箱的过程中
不允许将矩形物品斜着放
(PS:下图就是不允许的装箱操作),同时在装箱过程中允许将物品旋转90度放置(但是为了简单地求解问题,
我们规定不允许将物品旋转90度
),一般来说求解的目标是最小化箱子的使用数目。本文采用
BL法全称是bottom-up left-justified求解。
⛄ 运行结果
⛄ 部分代码展示
%% 计算物品在箱子中从右上角下降downH又向左移动leftW后,右上角顶点的坐标
% 输入itemRP:此时物品右上角顶点坐标[x,y]
% 输入downH: 物品item从右上角可以下降的最大高度
% 输入leftW: 物品item从右上角下降最大高度以后,可以向左移动的最大距离
% 输出itRPXY:物品item在箱子中下降downH又向左移动leftW后,右上角顶点的坐标
function itRPXY=Update_itemRP(itemRP,downH,leftW)
itRPXY=zeros(1,2); %储存物品item在箱子中下降downH又向左移动leftW后,右上角顶点的坐标
itRPXY(2)=itemRP(2)-downH; %y坐标
itRPXY(1)=itemRP(1)-leftW; %x坐标
end
⛄ 参考文献
[1] Kim W , Hong C . A Distributed Hybrid Algorithm for Composite Stock Cutting[J]. Applied Mathematics & Information Sciences, 2012, 6(2):661S-667S.
⛳️ 代码获取关注我
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料