观察经济社会活动往往需要用到多项统计指标,如考察国家宏观经济运行状况,通常会用到国内生产总值、失业率、居民消费价格、进出口等指标,这些指标间一般存在内在的联系,研究多项指标间的相互依赖关系和内在统计规律性是多元统计分析的基本内容。
一、基本概念
多元统计分析是经典统计学发展起来的一个分支,是一种多指标(也称多变量)综合分析方法,可以在多指标相互关联情况下分析其统计规律,在研究经济社会现象中具有广泛应用。
在研究经济社会现象时,会收集大量个体的多方面信息,特别是随着信息化发展,采集到个体数量和指标数量大为增加,比如网上商品交易系统采集到的信息涉及的用户数以亿计,指标数量成百上千,这些都增加了分析的难度。对这些规模宏大、复杂难辨的信息进行提炼简化,提取重要信息辅助决策,是多元统计分析的重要应用领域。同时,经济社会现象间往往存在紧密的联系,表现为统计指标之间存在相关性、因果关系等,使用多元统计分析有助于研究统计指标间的内在联系,发现经济社会现象的内在规律性。
在实际观测和调查中,统计指标的取值一般是随机的,因此统计指标可以用随机变量来表示,那么多个统计指标对应多个随机变量。而多个随机变量组成的数据集合称为随机向量,随机向量服从一定的统计分布,这是多元统计分析方法建立的重要基础。
二、常用方法
多元统计分析方法按照分析特点大致可以分为两类:一是描述性方法,主要从原始数据中提取重要信息,对系统主要特征进行研究,包括主成分分析、因子分析、聚类分析、对应分析等。二是解析性方法,主要是研究变量间相关关系、因果关系等,通过建立模型对变量间的关系认识定量化,包括多元回归分析、判别分析、典型相关分析等。
(一)描述性方法
1. 主成分分析
在研究多指标(变量)问题时,由于指标间存在一定相关性,导致信息冗余, 增加分析的难度。对此,主成分分析通过将原有的多个变量进行线性变换,组合成几个较少新的相互无相关性的综合变量,尽可能提取原有变量信息,达到指标简化目的。比如,在进行地区发展综合评价时,往往会选取经济增长、科技创新、人民生活、生态环境等多项指标,而这些指标往往存在相关性,通过主成分分析将这些指标简化为一到两个综合指标,将有助于降低综合评价难度。
2. 因子分析
因子分析是主成分分析的推广,将具有复杂关系的多变量转化为数量较少的几个综合变量,从而用有限个不可观测的隐变量来解释原始变量间相关关系。比如,在研究人体交感神经和副交感神经对人体的影响时,通常采集收缩压、舒张压、心跳间隔、呼吸间隔、舌下温度 5 个指标,通过因子分析可以将这 5 个指标综合为两个隐变量指标,从而反映交感神经和副交感神经的影响,找到其与原始 5 个指标的联系。
3. 聚类分析
聚类分析是将具有相似特征的个体归为一类,从而使同类的个体相似性较高, 而不同类的个体之间差异较大。衡量个体之间相似性采用“距离”测度和相似系数, 常用的“距离”测度有明式距离、马氏距离、兰氏距离,常用的相似系数有夹角余弦、相关系数。聚类分析中常用的方法有系统聚类、动态聚类等。比如,对全国省区市经济类型进行分类时,一般会选取一些的经济指标,然后利用这些经济指标计算地区与地区之间的“距离”,将“距离”近的地区归为一类,将“距离” 远的地区归为不同类别,从而形成不同地区经济发展水平类别,深化对地区经济的认识。
(二)解析性方法
1. 多元回归分析
多元回归分析是研究一个因变量与多个解释变量之间相互依存关系,揭示因变量与解释变量间的数量关系,从而对因变量进行估计或预测。比如,在预测长期经济增长趋势时,通常使用国内生产总值作为因变量,资本存量、就业人数、人力资本存量、制度变量等作为自变量,利用多元回归方法建立经济增长与相关因素的定量模型,利用得到的模型关系对未来经济增长趋势进行预测。
2. 判别分析
判别分析是判别观察个体所属类别的一种统计分析方法,它是在已知观察个体分为若干个类别的条件下,通过建立判别规则,对观察个体进行判别分类。它与聚类分析最大不同是,聚类分析事先不知道观察个体有多少个类别,而判别分析事先已知观察个体的类别个数。常用的判别分析法有距离判别法、费舍尔判别法、贝叶斯判别法等。比如,世界银行将全球国家划分为高收入国家、中高收入国家、中低收入国家、低收入国家四种类型,当判断一个国家属于哪种类型时, 可以使用判别分析方法建立规则进行判别。
为分析中国经济增长的驱动因素及其影响,基于柯布—道格拉斯生产函数, 建立多元回归测算模型:
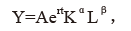 其中,Y、K、L 分别为总产出、资本投入、劳动投入,r 为技术进步率、t 为时间,α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数,将其设定为
其中,Y、K、L 分别为总产出、资本投入、劳动投入,r 为技术进步率、t 为时间,α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数,将其设定为
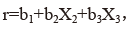 ,其中分别
,其中分别
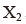 和
和
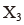 为第二产业和第三产业就业人员比例,带入上述生产函数,并假定规模报酬不变,即 α+β=1,可以得到:
为第二产业和第三产业就业人员比例,带入上述生产函数,并假定规模报酬不变,即 α+β=1,可以得到:
观察经济社会活动往往需要用到多项统计指标,如考察国家宏观经济运行状况,通常会用到国内生产总值、失业率、居民消费价格、进出口等指标,这些指标间一般存在内在的联系,研究多项指标间的相互依赖关系和内在统计规律性是多元统计分析的基本内容。
一、基本概念
多元统计分析是经典统计学发展起来的一个分支,是一种多指标(也称多变量)综合分析方法,可以在多指标相互关联情况下分析其统计规律,在研究经济社会现象中具有广泛应用。
在研究经济社会现象时,会收集大量个体的多方面信息,特别是随着信息化发展,采集到个体数量和指标数量大为增加,比如网上商品交易系统采集到的信息涉及的用户数以亿计,指标数量成百上千,这些都增加了分析的难度。对这些规模宏大、复杂难辨的信息进行提炼简化,提取重要信息辅助决策,是多元统计分析的重要应用领域。同时,经济社会现象间往往存在紧密的联系,表现为统计指标之间存在相关性、因果关系等,使用多元统计分析有助于研究统计指标间的内在联系,发现经济社会现象的内在规律性。
在实际观测和调查中,统计指标的取值一般是随机的,因此统计指标可以用随机变量来表示,那么多个统计指标对应多个随机变量。而多个随机变量组成的数据集合称为随机向量,随机向量服从一定的统计分布,这是多元统计分析方法建立的重要基础。
二、常用方法
多元统计分析方法按照分析特点大致可以分为两类:一是描述性方法,主要从原始数据中提取重要信息,对系统主要特征进行研究,包括主成分分析、因子分析、聚类分析、对应分析等。二是解析性方法,主要是研究变量间相关关系、因果关系等,通过建立模型对变量间的关系认识定量化,包括多元回归分析、判别分析、典型相关分析等。
(一)描述性方法
1. 主成分分析
在研究多指标(变量)问题时,由于指标间存在一定相关性,导致信息冗余, 增加分析的难度。对此,主成分分析通过将原有的多个变量进行线性变换,组合成几个较少新的相互无相关性的综合变量,尽可能提取原有变量信息,达到指标简化目的。比如,在进行地区发展综合评价时,往往会选取经济增长、科技创新、人民生活、生态环境等多项指标,而这些指标往往存在相关性,通过主成分分析将这些指标简化为一到两个综合指标,将有助于降低综合评价难度。
2. 因子分析
因子分析是主成分分析的推广,将具有复杂关系的多变量转化为数量较少的几个综合变量,从而用有限个不可观测的隐变量来解释原始变量间相关关系。比如,在研究人体交感神经和副交感神经对人体的影响时,通常采集收缩压、舒张压、心跳间隔、呼吸间隔、舌下温度 5 个指标,通过因子分析可以将这 5 个指标综合为两个隐变量指标,从而反映交感神经和副交感神经的影响,找到其与原始 5 个指标的联系。
3. 聚类分析
聚类分析是将具有相似特征的个体归为一类,从而使同类的个体相似性较高, 而不同类的个体之间差异较大。衡量个体之间相似性采用“距离”测度和相似系数, 常用的“距离”测度有明式距离、马氏距离、兰氏距离,常用的相似系数有夹角余弦、相关系数。聚类分析中常用的方法有系统聚类、动态聚类等。比如,对全国省区市经济类型进行分类时,一般会选取一些的经济指标,然后利用这些经济指标计算地区与地区之间的“距离”,将“距离”近的地区归为一类,将“距离” 远的地区归为不同类别,从而形成不同地区经济发展水平类别,深化对地区经济的认识。
(二)解析性方法
1. 多元回归分析
多元回归分析是研究一个因变量与多个解释变量之间相互依存关系,揭示因变量与解释变量间的数量关系,从而对因变量进行估计或预测。比如,在预测长期经济增长趋势时,通常使用国内生产总值作为因变量,资本存量、就业人数、人力资本存量、制度变量等作为自变量,利用多元回归方法建立经济增长与相关因素的定量模型,利用得到的模型关系对未来经济增长趋势进行预测。
2. 判别分析
判别分析是判别观察个体所属类别的一种统计分析方法,它是在已知观察个体分为若干个类别的条件下,通过建立判别规则,对观察个体进行判别分类。它与聚类分析最大不同是,聚类分析事先不知道观察个体有多少个类别,而判别分析事先已知观察个体的类别个数。常用的判别分析法有距离判别法、费舍尔判别法、贝叶斯判别法等。比如,世界银行将全球国家划分为高收入国家、中高收入国家、中低收入国家、低收入国家四种类型,当判断一个国家属于哪种类型时, 可以使用判别分析方法建立规则进行判别。
为分析中国经济增长的驱动因素及其影响,基于柯布—道格拉斯生产函数, 建立多元回归测算模型:
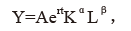 其中,Y、K、L 分别为总产出、资本投入、劳动投入,r 为技术进步率、t 为时间,α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数,将其设定为
其中,Y、K、L 分别为总产出、资本投入、劳动投入,r 为技术进步率、t 为时间,α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数,将其设定为
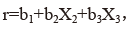 ,其中分别
,其中分别
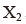 和
和
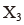 为第二产业和第三产业就业人员比例,带入上述生产函数,并假定规模报酬不变,即 α+β=1,可以得到:
为第二产业和第三产业就业人员比例,带入上述生产函数,并假定规模报酬不变,即 α+β=1,可以得到:
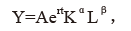 其中,Y、K、L 分别为总产出、资本投入、劳动投入,r 为技术进步率、t 为时间,α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数,将其设定为
其中,Y、K、L 分别为总产出、资本投入、劳动投入,r 为技术进步率、t 为时间,α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数,将其设定为
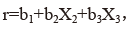 ,其中分别
,其中分别
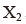 和
和
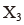 为第二产业和第三产业就业人员比例,带入上述生产函数,并假定规模报酬不变,即 α+β=1,可以得到:
为第二产业和第三产业就业人员比例,带入上述生产函数,并假定规模报酬不变,即 α+β=1,可以得到: