代数拓扑（一）

在上一篇《范畴与函子》中，我们初步了解了代数拓扑这门学科想要干什么，即通过找拓扑空间的具有代数结构的不变量来将拓扑空间进行分类，在这一篇，我们即将正式步入代数拓扑的城堡~

先列一下我们这一篇的任务目标：

• 函子（一）：两个道路连通空间同胚（或同伦等价），那么它们的基本群同构
• 函子（二）：两个拓扑空间同胚（或同伦等价），那么它们的奇异同调群同构

在具体展开前，我们先直观了解一下：什么是一个拓扑空间的基本群和同调群？

“基本群”和“同调群”是法国伟大的数学家庞加莱（Poincaré）引进的概念，两者都是用来窥测一个几何体（拓扑空间）的“中空”性质，或者说这个几何体有怎样的“洞”（即几维的“洞”）。例如一个游泳圈（二维环面），它中间有个空洞，因此它的基本群是非平凡的，一维、二维的同调群也是非平凡的。

不过，与同调群相比，基本群具有更直观的几何含义，这是由于它的定义更直观一些，然而这也给基本群带来很大的缺陷：基本群比同调群更难计算！

但在后期不断发展中，基本群与同调群逐渐演变推广到同伦群与一般系数（上）同调群的概念，（基本群实质是一维同伦群，这些推广我们将在下一章讨论）同时也催生了不少丰富的理论计算方法。

【一】基本群

这一章中，我们首先给出拓扑空间的第一个具有代数结构的不变量——基本群。

1.1基本群

【基本群】一个拓扑空间 X 中的任意一点 x_0 可以诱导一个 基本群 \pi_1(X,x_0) ，这个群是这样构成的：起点和终点都是 x_0 的道路 a 所构成的集合在一种划分下形成的等价类 [a] ，基本群就是由这些等价类 [a] 构成，并且称 [a] 为闭路类，其在复合意义下为一个群。那么如何划分这些闭路呢？如果两条闭路 定端同伦 ，那么它们就属于同一类。

【同伦与定端同伦】好了，什么是定端同伦？不急，我们先从同伦说起。可以直观理解一下，给两个拓扑空间 X 、 Y ，以及从 X 到 Y 的两个连续映射 f 、 g ，如果在某个时刻起， f(X) 在 Y 中开始连续变化，恰好又在另一个时刻变化到了 g(X) ，那么我们说映射 f 和 g 是 同伦 的。想象一下，如果 f 、 g 是 Y 中的两条道路（此时 X 为单位区间 I=[0,1] ），那么 f 和 g 同伦（记为 f\simeq g ）的直观含义就是： Y 在 f 下的道路 f(X) 可以连续变化到 Y 在 g 下的道路 g(X) 。严格定义是，再存在一个连续映射 H:I\times X\rightarrow Y ，使得 H(0,x)=f(x) 且 H(1,x)=g(x) ，那么 f 与 g 同伦。 f 和 g 定端同伦 说的是，道路 f(X) 变化到道路 g(X) 的过程中，起点和终点始终保持不变，也就是“定端”的含义。

【同伦等价与形变收缩核】由于在1.3节中要讨论同伦不变性，因此在这里说一下什么是同伦等价，以及一种特殊却最常见的同伦等价——形变收缩。如果说同伦是针对两个映射而言，那么同伦等价便是针对两个拓扑空间而言。两个拓扑空间 X 、 Y 同伦等价 （记为 X\simeq Y ）是指：存在连续映射 f:X\rightarrow Y 以及 g:Y\rightarrow X ，使得 g\circ f 和恒同映射 id_X 同伦， f\circ g 和 id_Y 同伦。并且此时也称 f 是 X 到 Y 的一个同伦等价。这样不太好直观理解，但是可以考虑比较特殊的同伦等价—— 形变收缩 ： A 是 X 的子空间， X 可以形变收缩到 A 要求， X 和 A 同伦等价，并且此时 f 为一个收缩映射 r ， g 固定为包含映射 i 。可以理解为 X 可以“连续”收缩到 A ，此时称 A 为 X 的形变收缩核。

注1：同胚一定同伦等价！

注2：道路连通空间 X 每一点的基本群同构，因此可以直接说 X 的基本群是 \pi_1(X) 。

1.2 函子性质

函子性质是描述拓扑空间的有代数结构的不变量的非常重要的语言，在上一篇《范畴与函子》中也讨论过。一般地，两个拓扑空间有连续映射，那么可以诱导出它们在对应点的基本群同态，并且若这两个拓扑空间同胚，那么它们对应点的基本群同构。为了方便用范畴语言描述，这里给出 道路连通 的拓扑空间范畴和群范畴之间的函子：

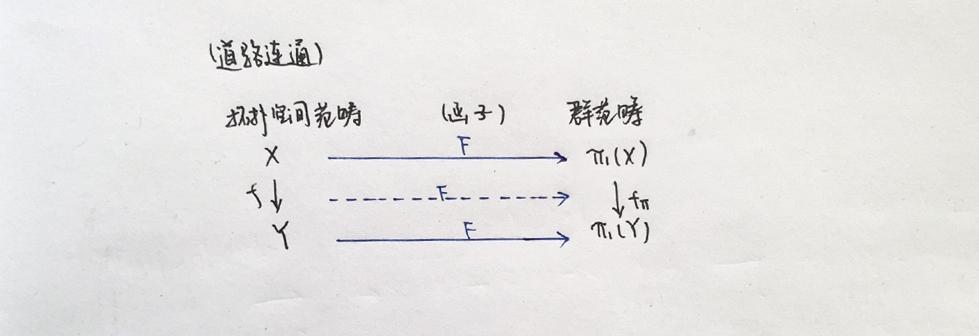
【协变函子】道路连通的拓扑空间范畴和群范畴之间存在协变函子，这个函子把对象拓扑空间映射到它的基本群（是群范畴中的一个对象），并且把两个拓扑空间 X 、 Y 之间的态射 f （连续映射）映到它们的基本群 \pi_1(X) 、 \pi_1(Y) 之间的态射 f_\pi （群同态）。并且由上一篇中函子的性质1可以知道，当 f 为同胚时， f_\pi 为同构。

注：对 [a]\in\pi_1(X) ， f_\pi ([a]):= [f\circ a] 。

1.3 同伦不变性

设拓扑空间 X 与 Y 道路连通 ，则：

（1）映射的同伦：如果 f \simeq g ，那么 f_\pi = g_\pi ；

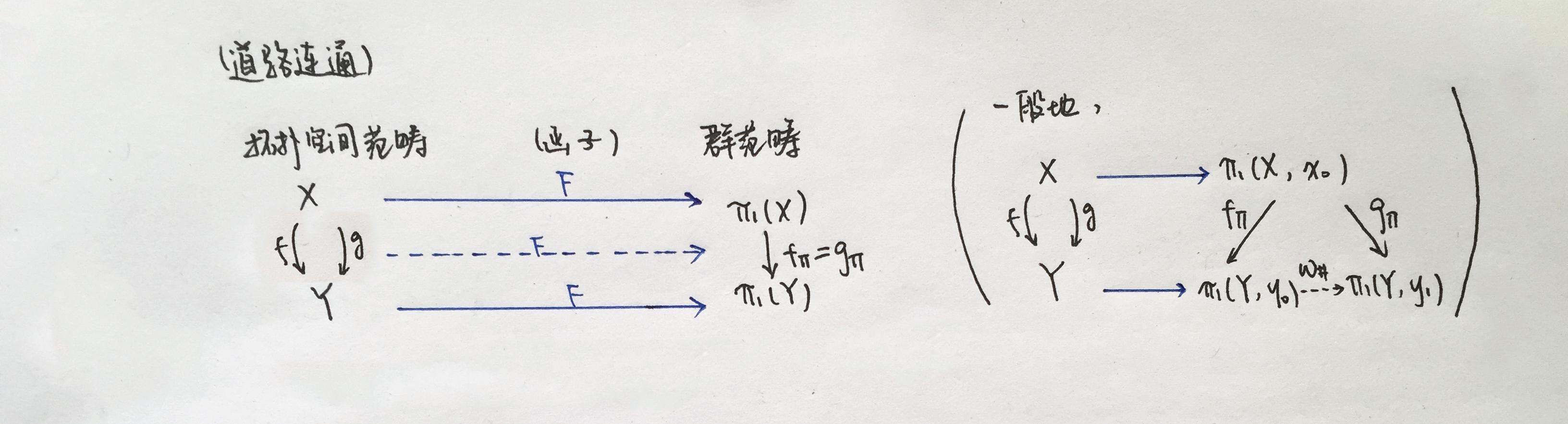
注：如果 X 非道路连通，则 f_\pi 和 g_\pi 仅相差一个同构 \omega _\# 。

（2）Cor：拓扑空间的同伦等价：如果 f:X\simeq Y ，那么 f_\pi:\pi_1(X)\cong \pi_1(Y) 。

1.4 计算方法

【Van-Kampen定理】 主要计算一类特殊的拓扑空间 X=X_1\cup X_2 的基本群，例如圆束 \bigvee_{i=1}^{n} {\bf{S}}_i^1 ，以及一般的闭曲面的基本群。思想是：通过 \pi_1(X_1\cap X_2,x_0) 、 \pi_1(X_1,x_0) 、 \pi_1(X_2,x_0) 来计算 \pi_1(X,x_0) 。

1.5 例子

• 1维圆周 {\bf{S}} ^1 的基本群： \pi_1({\bf{S}}^1) \cong {\bf{Z}} （ n>1 维球面由于单连通因此基本群平凡）；
• n 维实射影空间 {\bf{P}}^n （ n>1 ）的基本群： \pi_1({\bf{P}}^n)\cong{\bf{Z}}_2 ；
• n 维环面 {\bf{T}} ^n （ n>1 ）的基本群： \pi_1({\bf{T}} ^n)\cong \underbrace {{\bf{Z}} \oplus {\bf{Z}} \oplus ...\oplus{\bf{Z}} }_n ；
• 2维可定向闭曲面 n{\bf{T}}^2 的基本群交换化： \tilde{\pi_1(n {\bf {T}} ^2)}\cong \underbrace {{\bf{Z}}\oplus{\bf{Z}}\oplus ...\oplus {\bf{Z}} }_{2n} ；
• 2维不可定向闭曲面 m{\bf{P}} ^2 的基本群交换化： \tilde{\pi_1(m {\bf {P}} ^2)}\cong\underbrace { {\bf {Z}} \oplus {\bf {Z}} \oplus ...\oplus {\bf {Z}} }_{m-1}\oplus {\bf {Z}} _2 。

【二】奇异同调群

上一章中我们知道了一个拓扑空间 X 在它的任一点 x_0 处可以诱导一个代数空间——基本群 \pi_1(X,x_0) ，这是第一个拓扑空间的有代数结构的不变量。在这一章中，我们将发现拓扑空间第二个具有代数结构的不变量——（ 整系数 ）奇异同调群！

2.1奇异同调群

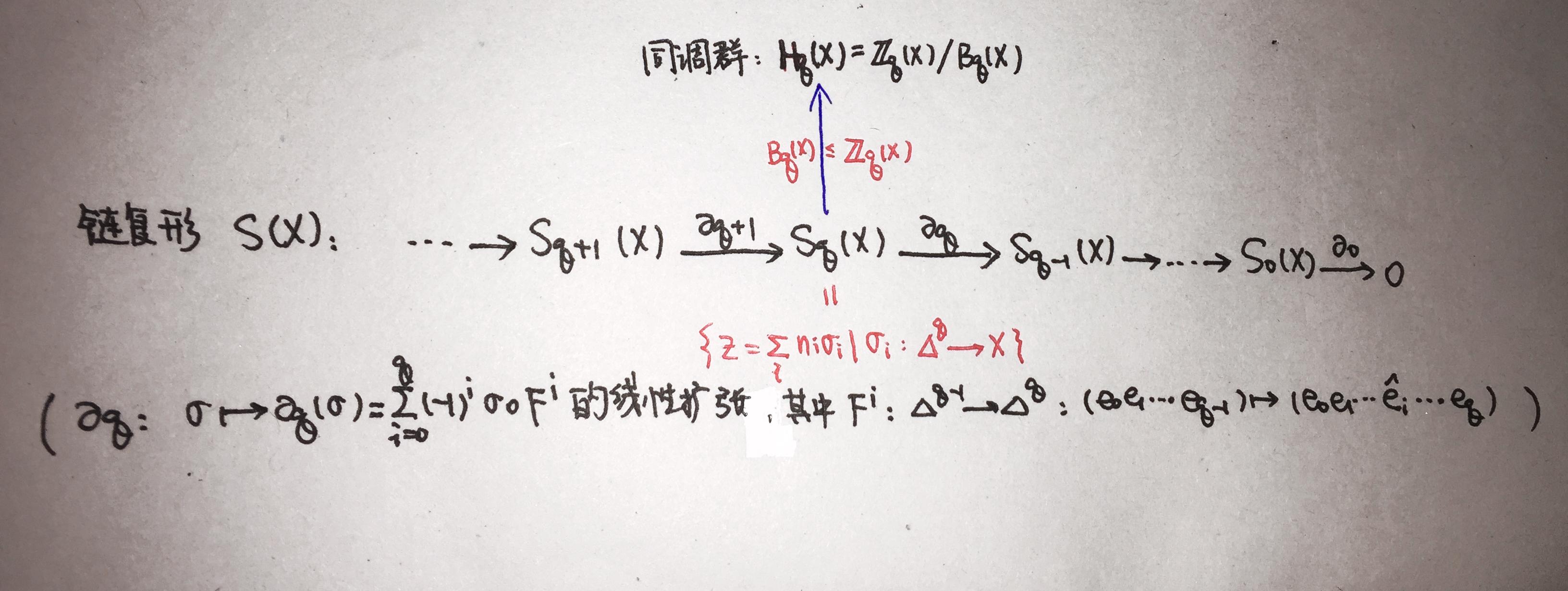
（如上图，所谓“同调”，实际上就是 “核模掉像” ）

【奇异链复形】如图，一个拓扑空间 X 的 奇异链复形 S_*(X) 是由一连串的 q 维奇异链群 S_q(X) 组成的一条同态链：

（1）每个 奇异链群 S_q(X) 是由 q 维奇异单形 \sigma 生成的Abel自由群，其中， q 维奇异单形 \sigma 是从标准单形 \Delta ^q 到 X 的一个 连续 映射（一维奇异单形是 X 中的一条道路）， S_q(X) 中元素称为 q 维奇异链（奇异单形一定是奇异链，奇异链群由奇异链组成）；

注（标准单形）： \Delta ^q:=\{\lambda_0e_0+\cdots+\lambda_qe_q:\lambda_i\ge 0,\sum_{i=0}^q\lambda_i=1\} 称为标准单形， e_0 为零点， \{e_i\}_{i=1}^\infty 为 \bf R^\infty 的规范正交基。直观来说， \Delta^0 为点， \Delta^1 为线段， \Delta^2 为三角形， \Delta^3 为四面体。

（2） 链群之间的同态映射 \partial_q 称为 边缘同态 ，且 \partial_{q+1}\circ \partial_q=0 （这样保证了 Im\ \partial_{q+1}\leq Ker\ \partial_q ）。

【奇异同调群】 给了 X 的一个链复形后，就可以定义 X 的奇异同调群了：

（1） 闭链群 {\bf {Z}} _{q}(X) ： {\bf {Z}} _q(X):= Ker\ \partial_q ，且称其中的元素为一个闭链；

（2） 边缘链群 B_{q}(X) ： B_{q}(X):=Im\ \partial_{q+1} ，且称其中的元素为一个边缘；

（3） 奇异同调群 H_q(X) ： H_{q}(X):= {\bf {Z}}_{q}(X)/B_{q}(X) ，其中元素 [z] 为同调类，若 [z_1]=[z_2] ，则称闭链 z_1 和闭链 z_2 同调（此时 z_1-z_2\in B_q(X) ），因此也可以 把闭链看作同调群中的元素 。

【理解】 q 维同调群中， 两个闭链同调，当且仅当它们的差是某个 q+1 维闭链的边缘 。 道路连通 空间 X 的低维同调群（ H_0(X) 、 H_1(X) ）可以直观理解，再高维就很难直观想象了：

（1） H_0(X) 中，奇异单形 x 和 y （ X 中两个点）同调，当且仅当它们的差 y-x 是某个1维奇异链的边缘，若取1维奇异链 \sigma 为 x 到 y 的道路（奇异单形），那么经过计算恰好可以得出 \partial _1(\sigma)=y-x ，因此，奇异单形 x 和 y 是同调的，所以 H_0(X) 中的元素（同调类）为 kx （ k\in {\bf {Z}} ），因此 X 道路连通时， H_0(X)\cong {\bf {Z}} （若 X 有 n 个道路分支，则 H_0(X)\cong \underbrace { {\bf {Z}} \oplus {\bf {Z}} \oplus ...\oplus {\bf {Z}} }_n ）；

注：一般我们会考虑 X 的 约化同调群 \tilde{H_q}(X) ，与 H_q(X) 唯一不同在：零维同调群 H_0(X)=\tilde{H_0}(X)\oplus{\bf {Z}} 。因此，拓扑空间的约化同调群能更好地描述这个拓扑空间有几维的“洞”（因为道路连通的拓扑空间没有零维的洞，此时它的零维约化同调群也为零）。

（2） H_1(X) 中，奇异单形 \sigma 和 \tau （ X 中两条定端同伦的闭路）同调，当且仅当它们的差 \tau -\sigma 是某个2维奇异链的边缘，我们可以利用同伦构造一个2维奇异链，也恰好使得它的边缘等于 \tau -\sigma ，因此，奇异单形 \sigma 和 \tau 是同调的，但对于 H_1(X) 中一般的闭链我们不知道是不是同调的，所以换个思路：由上述分析可知， X 的基本群 \pi_1(X,x) 到1维同调群 H_1(X) 有个映射 p ，且是满同态，因此 H_1(X)\cong\pi_1(X,x)/Ker\ p ，而恰好可以证明， Ker\ p=\pi_1'(X,x) （换位子群），所以 X 道路连通时， H_1(X)\cong\pi_1(X,x)/\pi_1'(X,x) ，即 基本群的交换化 ；

（3）如果 X 为 单点集 ，那么很容易可以算出:

H_q(X)\cong \left\{ \begin{aligned}{\bf {Z}} &\ ,& q=0 \\ 0 & \ , & q>0 \end{aligned} \right. 。

2.2 函子性质

链复形只是连接拓扑空间和它的同调群的一个桥梁，我们真正要得到的是“同调群是拓扑空间的有代数结构的不变量”这一性质，也就是拓扑空间范畴和Abel群范畴之间的函子关系：

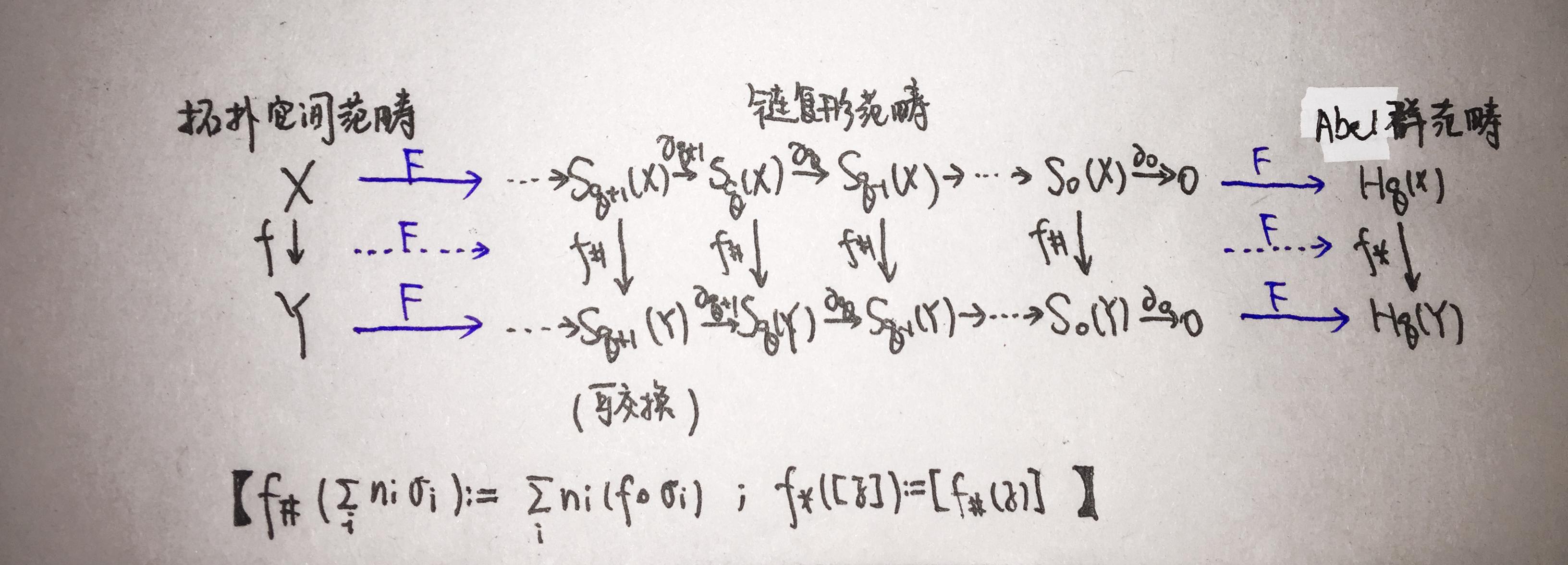
【协变函子】拓扑空间范畴和链复形范畴之间存在协变函子，链复形范畴与Abel群范畴之间存在协变函子，因此由上一篇中函子的性质2可以知道，拓扑空间范畴和Abel群范畴之间有协变函子，即这个函子把对象拓扑空间映射到它的奇异同调群（是Abel群范畴中的一个对象），并且把两个拓扑空间 X 、 Y 的态射 f （连续映射）映到它们奇异同调群 H_q(X) 、 H_q(Y) 间的态射 f_* （群同态）。并且，当 f 为同胚时， f_* 为同构。

2.3 同伦不变性

由于同胚这个条件比较强，所以我们看看如果上述的 f 是同伦等价时， f_* 是不是同构。不过我们还需引入一个概念：链复形之间的链同伦。

即：称两个链复形 C 与 D 之间的链映射 f 与 g 是链同伦，如果存在一系列Abel群同态 H_n:C_n\rightarrow D_n ，使得 f_n-g_n=\partial_{n+1}\circ H_n+H_{n-1}\circ\partial_n （可参看下图理解），记为 f\simeq g ；称两个链复形链同伦等价，如果存在 f:C\rightarrow D ， g:D\rightarrow C ，使得 g\circ f\simeq 1 且 f\circ g\simeq 1 ，此时记 C\simeq D 。

类似基本群中的同伦不变性，我们有：

（1） 映射的同伦：如果 f\simeq g ，那么 f_\#\simeq g_\# ，因而 f_*=g_*

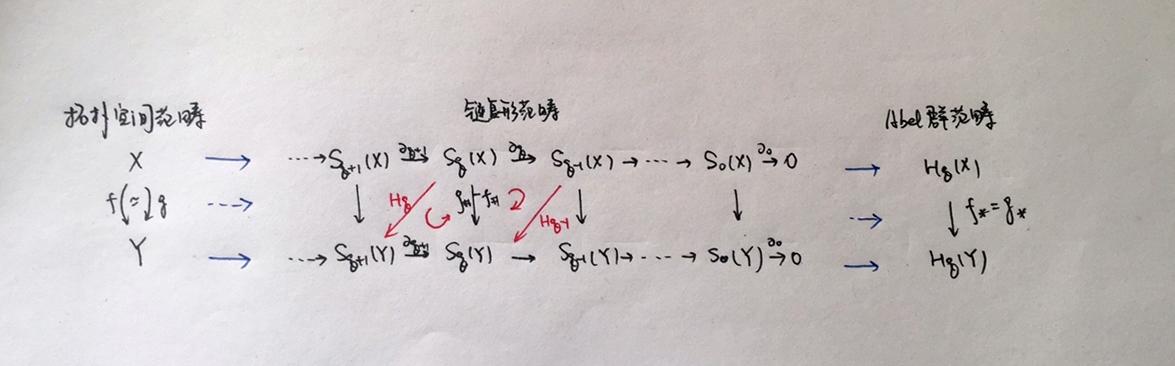
（2）Cor：拓扑空间的同伦等价：如果 f:X\simeq Y ，那么 f_\#:S_*(X)\simeq S_*(Y) ，因而 f_*:H_q(X)\cong H_q(Y) 。

2.4 计算方法

以下三种计算方法的证明都用到了 《同调代数》 中链复形与其同调群之间函子的特殊性质： 链复形的短正合序列可诱导出其同调群的长正合序列 。

【空间偶：长正合序列】 为了计算同调群，我们想要把 X 的所有维同调群 H_q(X) 类似链复形一样用一条链串联在一起 ，可以参考下图：

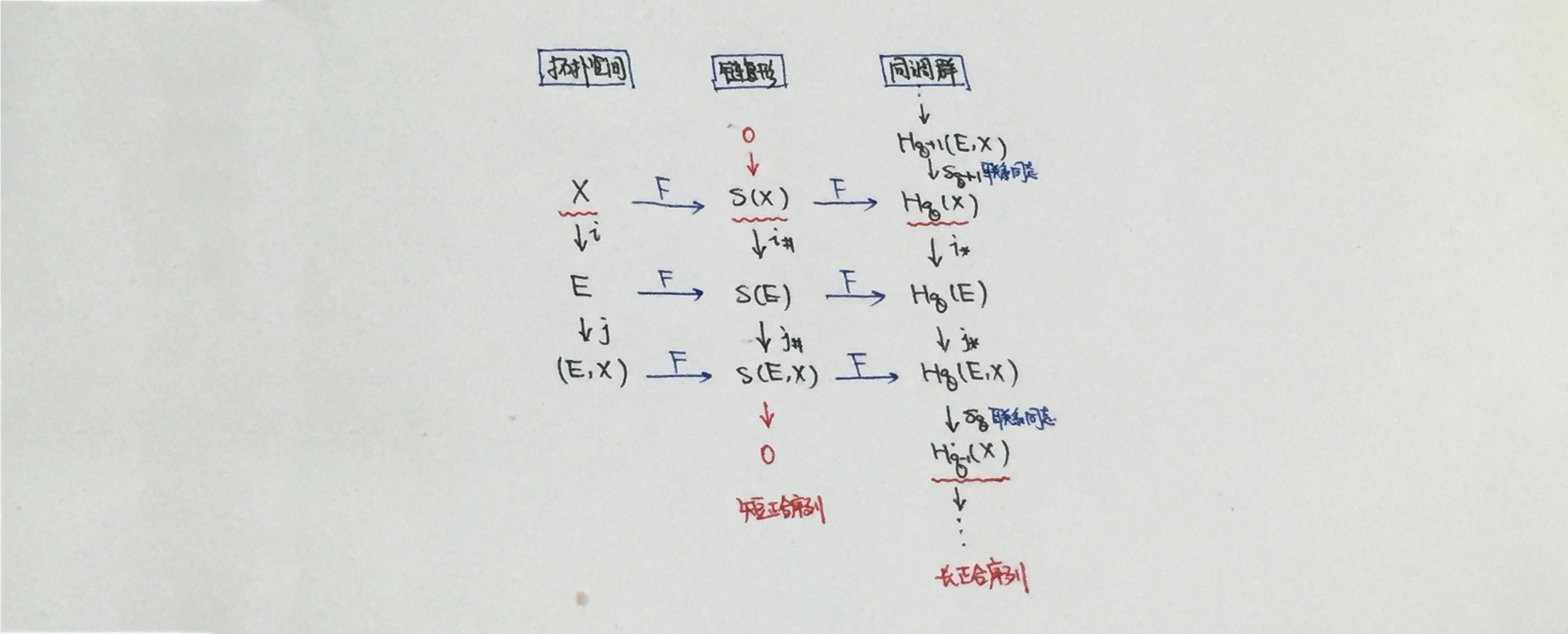
这样利用追图法就可以计算出一些同调群了：如果能 E 相对于 X 的空间偶 (E,X) 导出一个同调群的 长正合序列 ，那么我们就得到了 X 的不同维数同调群之间的关系，并利用正合性和追图法计算 X 的部分同调群，其计算的 核心之处在于利用“核等于像” 。

注1：某个范畴中，一个关于对象和态射的序列 ... \ \underrightarrow {f_{n+2}}\ C_{n+1}\ \underrightarrow {f_{n+1}}\ C_n\ \underrightarrow {f_n}\ C_{n-1}\ \underrightarrow {f_{n-1}}\ ... ，如果 Im\ f_{n+1}=Ker\ f_n ，则称这个序列为 正合序列 。若正合序列仅有五项，即 0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0 ，则称该序列为 短正合序列 。

注2：空间偶 (X,A) 的链复形 S_q(X,A) 以及同调群 H_q(X,A) 的导出类似于普通拓扑空间中的做法，且 S_q(X,A)=S_q(X)/S_q(A) ，其中 A\subset X 。

【空间偶：切除定理】 仅仅利用长正合序列定理似乎还不够，例如求 n 维球面 {\bf{S}}^n 的同调群，因此我们还需要一个辅助的定理来联系两个 长正合序列 算出更多一些的同调群。切除定理是说一个空间偶和它切掉性质比较好的一部分形成的另一个空间偶同构：

再看上图，用切除定理计算的实质就是 构造另一个空间偶的 长正合序列 (X,A) ，如果利用切除定理得到这两个序列中的 H_q(E,X) 与 H_q(X,A) 同构，那么这两条序列就有了“羁绊”，可以试着反复追图求 X 的在 长正合序列 中求不出来的同调群了。（利用此方法可以求出 {\bf{S}}^n 的各维同调群

【正合三元组：Mayer-Vietoris序列】 这个定理可以由切除定理导出，也可以利用它推出切除定理（因为切除定理中可以令 X_1= \mathring{A} ， X_2=X\backslash \overline{U} ），M-V序列也是由链复形的短正合序列导出了同调群的长正合序列，最终得到了下图的结论：

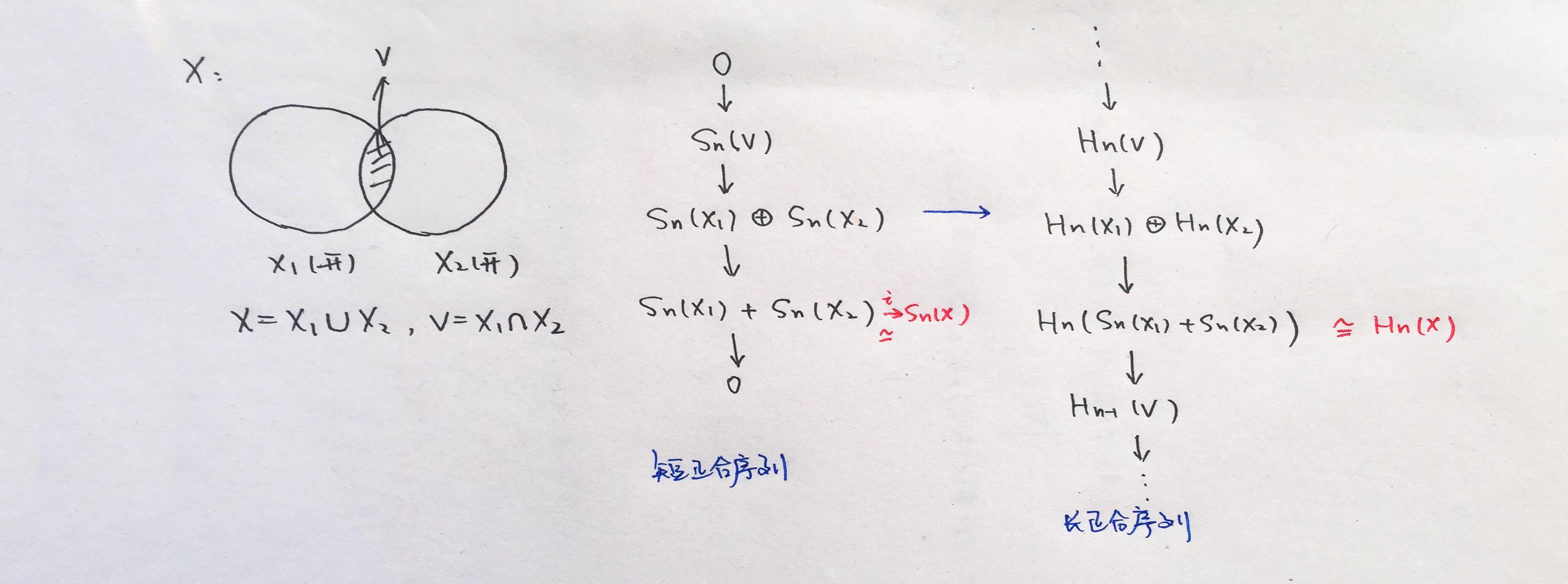
其应用类似于Van-Kampen定理的应用，计算一类特殊的拓扑空间 X=X_1\cup X_2 的同调群：即构造一个关于 X_1\cup X_2 、 X_1 、 X_2 和 X 的 M-V正合序列 ，通过 H_q(X_1\cap X_2) 、 H_q(X_1) 、 H_q(X_2) 来算出 H_q(X) 。（环面的同调群就是利用这个定理算出来的）

2.5 例子

• n 维球面 {\bf {S}} ^n （ n>1 ）的同调群： H_q({\bf{S}} ^n)\cong \left\{ \begin{aligned} {\bf{Z}} &\ ,& q=0,n \\ 0 & \ , & other \end{aligned} \right. ；
• n 维实射影空间 {\bf {P}} ^n （ n>1 ） 的同调群： H_q({\bf {P}} ^n)\cong \left\{ \begin{aligned} &{\bf {Z}} \ ,& q=0,or\ q=n=odd \\ &{\bf {Z}}_{2} \ , & 0<q<n\ \&\ q\ is\ odd \\ &0\ ,& other\end{aligned} \right. ；
• 2维环面 {\bf {T}} ^2={\bf {S}} ^1\times {\bf {S}} ^1 的同调群： H_q({\bf {T}} ^2)\cong \left\{ \begin{aligned} &{\bf {Z}} \ ,& q=0,2 \\ &{\bf {Z}}\oplus {\bf {Z}}\ , & q=1 \\ &0\ ,& other\end{aligned} \right. ；
• 2维可定向闭曲面 n{\bf {T}}^2 的同调群： H_q(n{\bf {T}}^2)\cong \left\{ \begin{aligned} &{\bf {Z}} \ ,& q=0,2 \\ &\underbrace {{\bf {Z}} \oplus {\bf {Z}} \oplus ...\oplus {\bf {Z}} }_{2n} \ , & q=1 \\ &0\ ,& other\end{aligned} \right. ；
• 2维不可定向闭曲面 m{\bf {P}}^2 的同调群： H_q(m{\bf {P}} ^2)\cong \left\{ \begin{aligned} &{\bf {Z}} \ ,& q=0 \\ &\underbrace {{\bf {Z}} \oplus {\bf {Z}} \oplus ...\oplus {\bf {Z}}} _{m-1}\oplus {\bf {Z}} _{2} \ , & q=1 \\ &0\ ,& other\end{aligned} \right.

注：空间偶 ({\bf D}^{n},{\bf {S}}^{n-1}) （ n>1 ）的相对同调群： H_{q}({\bf D}^{n},{\bf {S}}^{n-1})\cong \left\{ \begin{aligned} {\bf {Z}} &\ ,& q=n \\ 0 & \ , & other \end{aligned} \right.

【附】紧流形的 Euler 示性数

对 m 维 紧 流形 M 来说，其为有限可剖分空间（见下述定义），从而我们可定义它的 Euler 示性数，再通过 Euler-Poincaré 公式证明它是一个同伦不变量（故也有类似的函子表达）。

1. 有限可剖分空间

首先，称 \sigma 为 M 上的一个 q 维 单形 ，如果 \sigma 是从标准单形 \Delta ^q 到 X 的一个 嵌入 映射。

令 X 是一个拓扑空间，如果 X 上存在一个由单形构成的集合 K ，满足：

（i）若单形 \sigma\in K ，则 \sigma 的任一个面也属于 K ；

（ii） K 中任意两个单形或者不相交，或者交于各自的一个面，

于是我们称 K 为 X 的一个 单纯复形 。

再若 K 中的元素作为集合覆盖 X ，则称 K 为 X 的一个 单纯剖分 ，此时称 X 为 可剖分空间 。

再若 K 中元素有限，则称 X 为 有限可剖分空间 。

例 ：流形是可剖分空间，紧流形是有限可剖分空间。

2. Euler 示性数

设 X 是有限可剖分空间， K 是 X 的一个单纯剖分，记 r_q 为 K 中 q 维单形的个数，则定义 X 上的 Euler 示性数 \chi(X):=\sum_{q}(-1)^qr_q 。通过后文的 Euler-Poincaré 公式我们可验证，其为同伦不变量，即两个有限可剖分空间同伦等价，则它们的 Euler 示性数相等。

例 ：三维凸多面体的二维表面 X 的 Euler 示性数 \chi(X)=r_0-r_1+r_2 ，其中， r_0 为顶点数， r_1 为棱数， r_2 为面数。

3. Betti 数

设 X 是有限可剖分空间， K 是 X 的一个单纯剖分，其为有限的，故可验证 X 的奇异同调群 H_q(X) 为有限生成 Abel 群，由《抽象代数》中有限生成 Abel 群的结构定理知， H_q(X) 有如下分解：

H_q(X)=\underbrace{{\bf Z}\oplus \cdots\oplus {\bf Z}}_{\beta_q}\oplus {\bf Z}_{p_1}\oplus\cdots\oplus {\bf Z}_{p_\tau} ，且 p_i|p_{i+1} 。

我们称 \beta_q 为 H_q(X) 的 Betti 数 ，其刻画了 X 的 q 维“洞”的个数。又称 {\bf Z}_{p_i} 为 H_q(X) 的挠子群， \tau_q 为 H_q(X) 的 挠子群个数 。

由下一篇中一般系数同调群与整系数同调群的关系，我们还可得到 Betti 数更好的刻画： \beta_q=\dim H_q(X;{\bf R}) 。

例 ：二维球面 {\bf S}^2 的 Betti 数为 \beta_q= \left\{ \begin{aligned} 1&\ ,& q=0,n \\ 0 & \ , & other \end{aligned} \right. 。

4. Euler-Poincaré 公式

设 X 是有限可剖分空间，则有 Euler-Poincaré 公式 ：

\begin{aligned} \chi(X)&=\sum_{q } (-1)^q\beta_q\\ &= \sum_{q } (-1)^q\dim H_q(X;{\bf R}) \end{aligned} 。

其联系了 X 的 Euler 示性数与 Betti 数的关系，从而由于 Betti 数为同伦不变量，故 Euler 示性数也为同伦不变量！

例 ：对三维凸多面体的二维表面 X 来说，由于其同伦等价于二维球面 {\bf S}^2 ，故它们的 Euler 示性数相等，从而有经典的欧拉定理： \chi(X)=r_0-r_1+r_2=2 。