高代随记(一)从判别式与结式到椭圆函数j不变量
前言
在学习模形式的时候,碰到关于Weierstrass p级数,以及Eisenstein级数组合而成的椭圆曲线。其中对于椭圆曲线,左边是一个关于x的三次方程,其“判别式”在上班平面中是一个尖点形式(常数项为0,权为12)。
然后回想起来,所谓的“判别式”好像就是 判别式 。。。。
于是乎,我就把之前学的东西拿出来翻翻,然后稍微添加一些椭圆函数上的探讨。
开始部分还是和跟高代部分比较近,最后一块通过(分析地)计算,得到一些判别式 本身的不变性质 ,然后用这个性质去得到 椭圆曲线的 j 不变量 。
整体上还是以 复习判别式 为主2333
(文中部分内容来源 高等代数(下册)——大学高等代数课程创新教材/丘维声 著 )
目录
- 二次方程求根公式
- 数域K上的判别式(discriminant)
- 再来看看结式(resultant)
- 椭圆函数和判别式不变量(invariance)
二次方程求根公式
我记得当我最开始接触判别式的时候,还是上初中。小时候一直热衷于去探索二次方程的求根公式( 小学的时候一直以为按照二次求根学好了,能求任意次,知道我上大学后听说了Galois理论。。。 )
回想我初中的时候,曾经花了我一上午时间研究“勾股定理”。( 我记得当时上午的课是:语文、历史之类的课,然后,自己底下偷偷拿尺子画线量直角三角形三条边,开始算。限于尺子刻度的问题,我曾判定勾股定理是某个“线性关系”23333,关键当时还自豪地跟数学老师炫耀(班主任)2333,没少挨呲儿 ) 。 (以下斜体字部分就写写我的“风流往事”2333)
对于 二次方程, ax^2+bx+c=0\\ 其中 a\ne 0 .做如下变换 \begin{align} x^2+\frac{b }{a}x+\frac{b^2}{4a^2}&=\frac{b^2}{4a^2}-\frac{c}{a}\\ (x+\frac{b }{2a})^2&=\frac{b^2-4ac}{4a^2} \end{align}\\ 这个变换。( 当初明明我用了很多时间去思考,然而还是被家里人泼冷水233,其实我听说过“跂而望矣,不如须臾之所学”,但是自己发现的“大定理”真心很激动,虽然现在不怎么激动了。。 )
于是能发现,等号右边可能会有小于零的情形,譬如令 b=1,a=1,c=1 的方程 x^2+ x+1=0\\ 在当时来说,还没有进行扩域扩张到 复数 ,所以要求 \frac{b^2-4ac}{4a^2} >0\\ 因为横线下面恒正,所以一般管横向上面这玩意叫 判别式(discriminant) ,记为 \Delta={b^2-4ac} \\
当然,那个二次方程求根公式也很显然地有 \begin{align} (x+\frac{b }{2a}) &=\frac{b^2-4ac}{4a^2} \\x+\frac{b }{2a}&=\pm\sqrt{\frac{b^2-4ac}{4a^2} }\\x&=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{align}\\ 其中可不失一般性地认为 a>0 .当然,这不是这篇文章的重点,所以到此为止了~
数域K上的判别式(discriminant)
从“说文解字”的角度来说,discriminant这个词是1857年由英国数学家James Joseph Sylvester所首先使用的。
- dis-=分开
- crimin-=separate
再根据这个上文该名称是在求根的背景下的,所以结合中文的翻译,可以理解为:判断是否有能够分开(distinct)的根。也就是说,一个代数方程的所有根是否都是有区别的。
为了引出一般性的结论,可以从上面的二次方程入手来说。根据代数基本定理,可以知道二次方程至多有两个根。所以将二次方程写成如下形式 (x-x_1)(x-x_2)=0\\ 接着通过变形能够发现 x^2-(x_1+x_2)x+x_1x_2=0\\ 有 x_1+x_2=-\frac{b}{a},x_1x_2=\frac{c}{a}\\
接着,咱们考虑如何确定一个方程是否有不同的根呢?直接构造个这样的式子,这就是判别式了(显然通过 \Delta=0 来判断两根重复): \Delta=(x_1-x_2)^2\\ 看他是否等于0就好了,等于0 肯定就是重根。接着,进一步计算,让一般二次方程的三个系数代替这两个根,则有 \begin{align}x_1^2+x_2^2-2x_1x_2&=(x_1+x_2)^2-4x_1x_2=(-\frac{b}{a})^2-4(\frac{c}{a})\\& \Rightarrow \frac{b^2-4ac}{a^2}\Rightarrow\Delta=b^2-4ac\end{align}\\
好,既然二次方程有了判别根是否有重复的方法,那么对已任意的n次多项式 f(x)= x^n+a_{n-1}x^{n-1}+...+a_1x+a_0\\ 在复数域中的 n 个根分别为 c_1,c_2,...,c_n\\ 所以是否有重根,当且仅当下面这个式子是否成立 \Delta=\prod_{1\le j<i\le n}(c_i-c_j)^2 =0\\ 同样地,将“根”替换为原来多项式中的系数,利用组合学的一些想法(也可以直接用 Vieta公式 ),能够得到 \begin{align}-a_{n-1}&=c_1+c_2+...+c_n =\sigma_1(c_1,c_2,...,c_n)\\ (-1)^{k}a_{n-k}&=\sum_{1\le j_1<...<j_k\le n}c_{j_1}c_{j_2}...c_{j_k}=\sigma_k(c_1,c_2,...)\\&\vdots \qquad\qquad\qquad\qquad\qquad\vdots\\ (-1)^na_0&=c_1c_2...c_n=\sigma_n(c_1,c_2,...,c_n)\end{align}\\ 其中,将 \sigma_k(x_1,x_2,...,x_n) 记为 对称多项式 。也就是说将多项式里面的几个未知元的位置随意排列组合,并不影响多项式的值。
那么如何替换呢?
我们将替换后的判别式记为 D(f) 则有 \begin{align}D(f)&=\prod_{1\le j< i\le n}(c_i-c_j)^2 \\&\xlongequal{Vandermonde}\left|\begin{matrix}1&1&...&1\\c_1&c_2&...&c_n\\c_1^2&c_2^2&...&c_n^2\\\vdots&\vdots&\quad&\vdots\\c_1^{n-1}&c_2^{n-1}&...&c_{n}^{n-1}\end{matrix}\right| \left|\begin{matrix}1&1&...&1\\c_1&c_2&...&c_n\\c_1^2&c_2^2&...&c_n^2\\\vdots&\vdots&\quad&\vdots\\c_1^{n-1}&c_2^{n-1}&...&c_{n}^{n-1}\end{matrix}\right| ^T\\&=\left|\begin{matrix}n&\sum_{i=1}^nc_i&...&\sum_{i=1}^nc_i^{n-1}\\\sum_{i=1}^nc_i&\sum_{i=1}^nc_i^2&...&\sum_{i=1}^nc_i^n \\\vdots&\vdots&\quad&\vdots\\\sum_{i=1}^nc_i^{n-1}&\sum_{i=1}^nc_i^n&...&\sum_{i=1}^nc_i^{2n-2}\end{matrix}\right| \\&=\left|\begin{matrix}s_0&s_1&...&s_{n-1}\\s_1&s_2&...&s_n \\\vdots&\vdots&\quad&\vdots\\s_{n-1}&s_n&...&s_{2n-2}\end{matrix}\right|\end{align}\\
其中( 幂和) 记为, s_k(x_1,x_2,...,x_n)=\sum_{i=1}^nx_i^k,k=0,1,2,...\\ 这显然也是对称多项式。根据 对称多项式基本定理 ,它可以被表示为对称多项式 \sigma_k,(k=1,...,n) 的某个n元多项式的形式。
所以可以用 \begin{align}-a_{n-1}&=c_1+c_2+...+c_n =\sigma_1(c_1,c_2,...,c_n)\\ (-1)^{k}a_{n-k}&=\sum_{1\le j_1<...<j_k\le n}c_{j_1}c_{j_2}...c_{j_k}=\sigma_k(c_1,c_2,...)\\&\vdots \qquad\qquad\qquad\qquad\qquad\vdots\\ (-1)^na_0&=c_1c_2...c_n=\sigma_n(c_1,c_2,...,c_n)\end{align}\\ 表示出来,也就是说,用多项式系数表示出来。
这里再给一个幂和 s_k 与多项式 \sigma_1,\sigma_2,...,\sigma_n 转化的公式,此处不给出证明了,
牛顿(Newton) 公式 在 K[x_1,x_2,...,x_n] 中,当 1\le k\le n 时,有 s_k-\sigma_1s_{k-1}+\sigma_2s_{k-2}+...+(-1)^{k-1}\sigma_{k-1}s_1+(-1)^{k}k\sigma_k=0\\ 当 k>n 时,则有 s_k-\sigma_1s_{k-1}+\sigma_2s_{k-2}+...+(-1)^{n-1}\sigma_{n-1}s_{k-n+1}+(-1)^{n} \sigma_n s_{k-n}=0\\
命题1 把幂和用初等对称多项式表示 s_k=\left|\begin{matrix}\sigma_1&1&0&0&0&0&...&0&0\\2\sigma_2&\sigma_1&1&0&0&0&...&0&0\\3\sigma_3&\sigma_2&\sigma_1&1&0&0&...&0&0\\4\sigma_4&\sigma_3&\sigma_2&\sigma_1&1&0&...&0&0\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\quad&\vdots&\vdots\\ (k-1)\sigma_{k-1}&\sigma_{k-2}&\sigma_{k-3}&\sigma_{k-4}&\sigma_{k-5}&\sigma_{k-6}&...&\sigma_1&1\\ k \sigma_{k }&\sigma_{k-1}&\sigma_{k-2}&\sigma_{k-3}&\sigma_{k-4}&\sigma_{k-5}&...&\sigma_2&\sigma_1 \end{matrix}\right|\\
以及
命题2 将初等多项式用幂和的表示 \sigma_k=\frac{1}{k!}\left|\begin{matrix}s_1&1&0&0&...&0&0\\s_2&s_1&2&0&...&0&0\\ s_3&s_2&s_1&3&...&0&0\\\vdots&\vdots&\vdots&\vdots&\quad&\vdots&\vdots \\s_{k-1}&s_{k-2}&s_{k-3}&s_{k-4}&...&s_{1}&k-1 \\s_{k}&s_{k-1}&s_{k-2}&s_{k-3}&...&s_{2}&s_{1} \end{matrix}\right|\\
以上三种命题证明方法就是多写几项,找个规律,然后归纳法证明就可以了(把他们都列出来确实需要花费点功夫。。。。)。
于是乎,
对于三次方程 x^3+a_1x+a_0=0\\ 来说,通过上面一坨公式可以计算得到 D(f)=\left|\begin{matrix} 3&0&-2a_1\\0&-2a_1&-3a_0\\-2a_1&-3a_0&2a_1^2\end{matrix}\right| =-4a_1^3-27a^2_0\\
看看,像不像椭圆函数中的 \Delta=c_1G_4^3+c_2G_6^2\\
(我说指数。。。)
再来看看结式(resultant)
结式的目的本身是以两个多项式是否有公因式的角度出发的。然后,能够发现他有如下的作用:
- 判断公共复根
- 二元多项式的公共零点
- 计算判别式(主要说说这个)
- 化曲线的参数方程为直角坐标方程
对于结式,可以从两个多项式的公因式(从而可以判断是否有公共根)的角度来开始说,譬如如下两个多项式 f(x)= x^n+a_{n-1}x^{n-1}+...+a_1x+a_0\\ g(x)= x^m+b_{m-1}x^{m-1}+...+b_1x+b_0\\ 然后,假设它们不互素,也就是说——有公共复根,也就是说有次数大于0的公因式 h(x) ,则存在 f_1(x),g_1(x)\in K[x] ,使得 f(x)=f_1(x)h(x),g(x)=g_1(x)h(x)\\ 由于 \deg d(x)>0 ,因此 \deg f_1(x)<\deg f(x)\le n,\deg g_1(x)<\deg g(x)\le m\\ 从而有 g_1f=f_1g\\ 再设 f_1(x)= u_0x^{n-1}+u_{1}x^{n-2}+...+ u_{n-1}\\ g_1(x)= v_0x^{m-1}+v_{ 1}x^{m-2}+... +v_{m-1}\\ 比较两边多项式的各次项系数,得 \begin{cases}a_0v_0&=b_0u_0\\a_1v_0+a_0v_0&=b_1u_0+b_0u_1\\ ... &...\quad ...\\ a_nv_{m-2}+a_{n-1}v_{m-1}&=b_mu_{n-2}+b_{m-1}u_{n-1}\\a_nv_{m-1}&=b_mu_{n-1}\end{cases}\\
由于 f(x)\ne 0,g(x)\ne0 ,因此 f_1(x)\ne0,g_1(x)\ne0 ,从而 (u_0,u_1,...,u_{n-1})\ne0,(v_0,v_1,...,v_{m-1})\ne0\\ 因此它的系数矩阵 A 的行列式等于0,从而 |A'|\ne0 ,即 \left | \begin{matrix}a_0&a_1&...&...&...&...&a_n\\ \quad&a_0&a_1&...&...&...&...&a_n\\ \quad&\quad&\quad&...&...&...&...&...\\ \quad&\quad&\quad&\quad&a_0&a_1&...&...&...&...&a_n\\b_0&b_1&...&...&...&b_m\\\quad&b_0&b_1&...&...&...&b_m\\\quad&\quad&\quad&\quad...&...&...&...&...&...\\\quad&\quad&\quad&\quad&\quad&\quad&b_0&b_1&...&...&b_m\end{matrix}\right|=0\\ 其中带a的有m行,带b的有n行。
然后管这个东西叫做 结式(resultant) 。
有如下定理
定理 f(x) 与 g(x) 是域 K[x] 中两个多项式,其中 n>0,m>0 ,则结式 \operatorname{Res}(f,g)=0 的充要条件为要么 a_0=b_0=0 ,要么有公共复根。
从而可以推出
定理 设 f(x) 是数域 K 上 n 次多项式,首项系数为 a_0 ,则 D(f)=(-1)^{\frac{n(n-1)}{2}}a_0^{-1}\operatorname{Res}(f,f')\\
然后接着拿它来算三次方程 4x^3+g_1x+g_2\\ 则有 D(f)=-\frac{1}{4}\left | \begin{matrix} 4&0&g_1&g_2\\ \quad&4&0&g_1&g_2\\ 12&0&g_1\\ \quad&12&0&g_1\\\quad&\quad&12&0&g_1\end{matrix}\right|=-16( 4a^3+ 27b^2)\\ (感觉这里计算有点问题,我回来再仔细算算。。。)
椭圆函数和判别式不变量(invariance)
这里面,接着判别式的背景,再从这一方面看看判别式,顺手说一点模形式的东西
对于椭圆函数,即形如 y^2=4x^3-g_1x-g_2\\ 之所以去掉二次方的项,是因为根据Vieta公式,对于 n 次多项式的 n-1 次项系数是其根之和,所以,对每一项不定元做一个平移,便可使其为0.
对于椭圆函数,它非奇的时候就如图所示(就是封面)
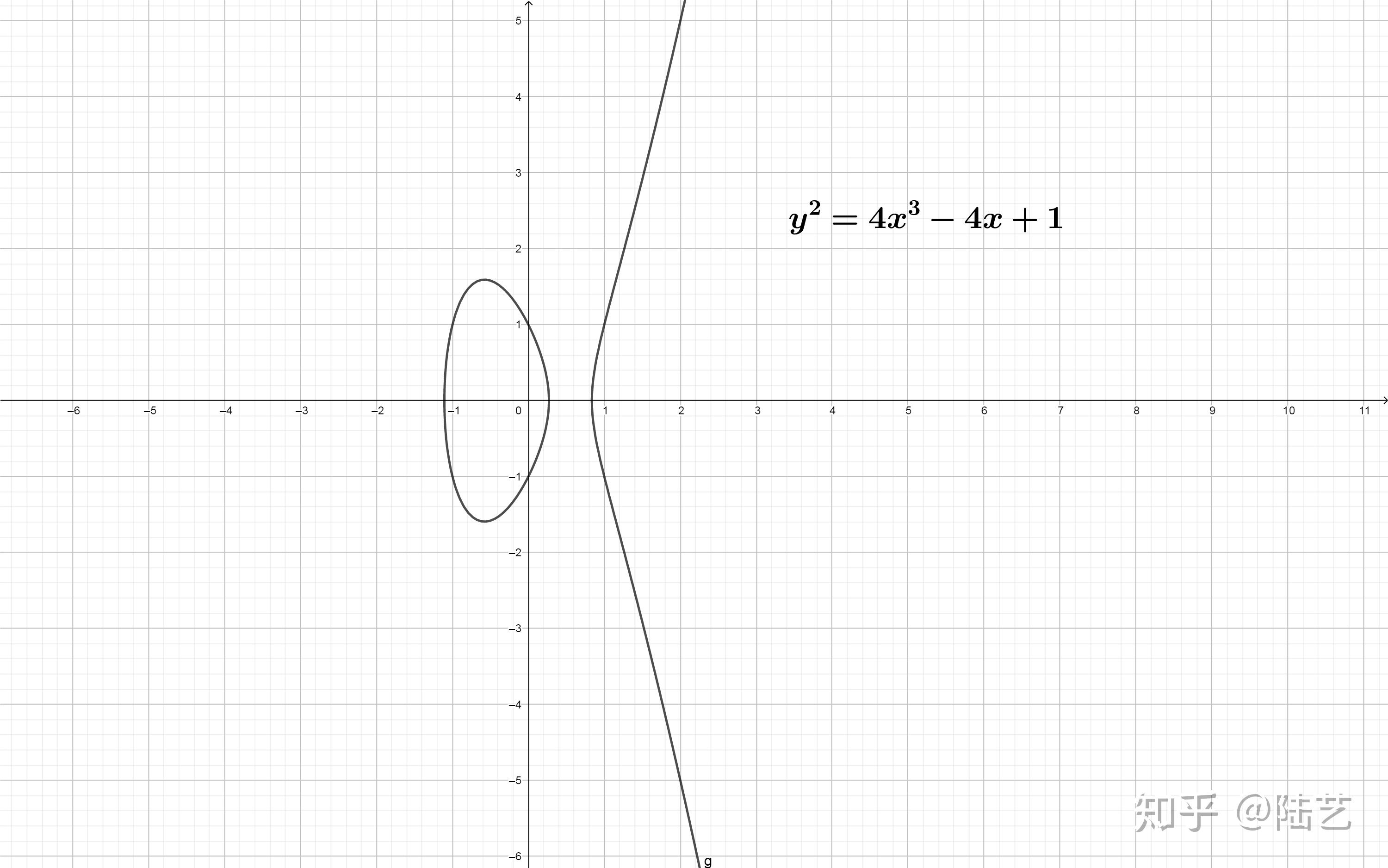
也就是说判别式不为0.
那为什么 判别式 \Delta=0 时,该曲线奇异呢 ?
可以算一下,假如右侧的判别式为0了,那么上面的椭圆函数可以写成如下的形式 y^2=4(x-a)^2(x+2a )\\ 对于代数曲线奇异的定义,在该文章中有所讲解
对两边求偏导,可以有微分 \operatorname{d}P = (4[2(x-a)(x+2a)+(x-a)^2],2y)\\ 其中,第一个分量为对 x 的微分 dx 系数,第二个分量为对 y 的微分 dy 的系数。
检验其是否为非奇,只需考虑 \operatorname{d}P=(0,0)\\ 是否成立。显然,对于 \begin{cases}x=a\\y=0\end{cases} 的时候上式成立(带入原方程去算y=0),所以有
判别式为0 \Leftrightarrow 为奇异的代数曲线
对于奇异点,当出现在椭圆函数上 时,就叫尖点(cusp)
这个也说明之前文章中,判别为非0与椭圆函数非奇异的关系
接下来,说说关于判别式的 不变量 性质。
- 平移不变性(Invariance of translation) : \operatorname{D}(P(x))=\operatorname{D}(P(x+\alpha))
- 相似不变性(Invariance by homothety) : \operatorname{D}(P(x))=\alpha^{n(n-1)}\operatorname{D}(P(\alpha x))
- 逆转不变性(Invariance by inversion) : \operatorname{D}(P(x))=\operatorname{D}(P^r(x))
注: P^r 为互反多项式,即 P^r(x)=x^nP(\frac{1}{x})
这几个可以借助几何的理解来看,
对于第一个,相当于把每一个根都沿着某方向平移 \alpha ,所以考虑判别式 \operatorname{D}(f(x))=\prod_{1\le j\le i\le n}(c_i-c_j)^2 \\ 显然不变(相消了)
对于第二个,就相当于考虑 \operatorname{D}(f(\alpha x))=\prod_{1\le j\le i\le n}\alpha^2 (\frac{c_i-c_j}{\alpha^2})^2 =\alpha^{n(n-1)}\operatorname{D}(f(x)) \\\\ 对于第三个方法同第二个的证明。
这三个不变性是判别式本身的不变性,下面看看域 K 上代数曲线 E 的判别式不变性是什么样的。
在域 K 上,一个Weierstrass 方程有如下形式 g^2=4x^3-g_2x-g_3\\ 其中 g_2,g_3\in K 。那么有判别式 \Delta=g_2^3-27g_3^2\in K\\
既然要看“不变性”,那么就要有“变”来衬托,所以进行一下变化 \begin{cases}x=u^2x'\\y=u^3y'\end{cases},u\in K\\ 于是乎,就有 u^6y'^2=4u^6x'^3-g_2u^2x'-g_3\\ 整理后则有 y'^2=4 x'^3-g'_2 x'-g’_3\\ 其中(可以借助上面的 相似不变性 得到下面) \begin{cases}g_2'=\frac{g_2}{u^4} \\g'_3=\frac{g_3}{u^6}\end{cases},\Delta\rightarrow\frac{\Delta'}{u^{12}}\\ 为了更好描述其不变性,用 j 不变量来对其进行描述 j(\tau)=\frac{12^3g_2^3(\tau)}{\Delta(\tau)}\\
注:
j 不变量 在这篇文章中出现
其实一开始还想能不能联系到 Ramanujan -Peterson conjecture 的,后来感觉,只是Dedekind eta 函数的24次方恰好满足判别式,而且conjecture的证明和判别式无关,后来也就没有往这方向发展了。
差不多就这些了~

