。

KL不等式作为收敛性分析中的一个重要研究工具，并且应用广泛。像半代数函数、tame函数、向量范数等等都是KL函数。早在1963年S. Łojasiewicz [7] 在实分析函数中，研究一般的最速下降曲线问题解的轨迹是否为有限长度时，提出Łojasiewicz不等式：

$$ 。并由此推导出最速下降曲线

的解的轨迹是有限长度，有界轨迹收敛到临界点。随后，Kurdyka [8] 将这一结果扩展到可在o-minimal结构中定义的可微函数中，相应的广义不等式称之为KL不等式。本文主要建立与其同解的无约束优化问题模型的KL性质，从而设计基于BB (Barzilai-Borwein)步长线搜索算法。

2. 预备知识

对于给定的广义实值函数 包含之前算过的所有目标函数值。综上所述，本文提出的算法是可行有效的。

5. 实验结果分析及讨论

通过MATLAB实验来证明该算法在重构信号方面的优势，实验运行平台的配置如下：Intel(R)Core (TM)i5-10400F CPU @2.90 GHz；内存16.00 GB。在不同的MATLAB版本测试下，结果不会发生较大变化。本文实验在MATLAB R2020b中进行。

实验取 ，a表示原始信号中非零元的个数。其中非零元的位置均是随机选取的，A是与高斯矩阵独立同分布的随机矩阵 [16]， 的高斯噪声，取 ，

时，则停止迭代。原始信号，观测向量及重构信号如 图1 所示。

比较 图1 中的(a)和(c)可以分析出来，所有的蓝点均被红点包围，这说明原始信号几乎被精确重构。上述实验表明，该算法效果良好，相对误差较小，为恢复大的稀疏信号提供了一种有效的方法。

本文在接下来的实验中，采用了4种不同的信号，对不同的算法进行比较分析。取上述实验中的初始参数，对NBBL1n和NBBL1这2种算法进行了对比和分析。在初始和终止条件相同的情况下，从函数值下降的角度分析，无论针对那种信号，NBBL1n算法下降总是最快的，迭代次数也最少，为进一步说明结果， 表1 和 表2 给出了详细的对比数据。由于设下随机种子，所以每次获取的信号是不变的。所以误差很小。

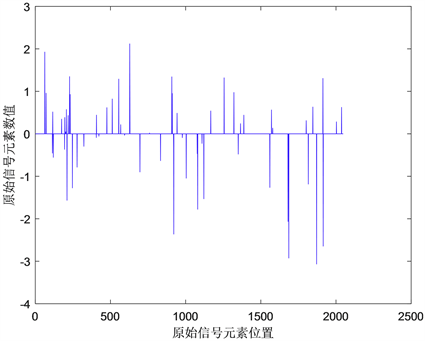
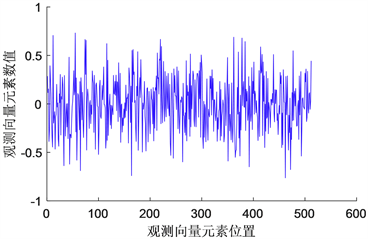
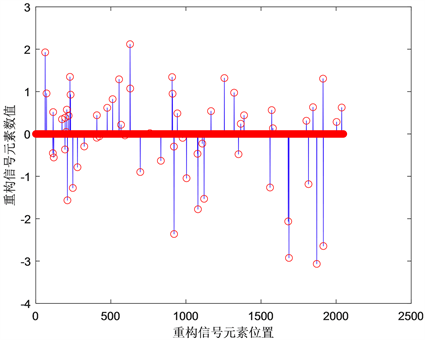
(a) 原始信号 (b) 观测向量 (c) NBBL1n (RelErr = 1.38%)

Figure 1 . The effectiveness of the NBBL1n algorithm

图1 . NBBL1n算法的有效性

表1 . 对于不同稀疏度，算法所需要的时间的迭代次数对比

表1 中详细的列出了4种不同信号的运行时间和迭代次数。从表中可以分析出，随着信号规模的不断增大，运行算法所需要的时间也明显增加，但是通过对比，新版本算法的运行总用时较少，迭代次数也比较少。