有限位势垒

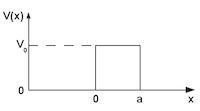
在量子力学里， 有限位势垒 是一种位势。在垒外，位势为 0 ，在垒内，位势为有限值 。 有限位势垒问题 专门研讨在这种位势的作用中，一个粒子的量子行为。如图右，最简单的有限位势垒是方形垒，垒高是一个常数。在这条目里，只研讨这种位势垒。

通常，在经典力学里，一维的有限位势垒问题会设定一个粒子，从位势垒的左边，往位势垒移动。假若，粒子的能量大于位势垒的位势。则这粒子，在经过位势垒的时候，因为动能的转换为势能，速度会降低，但方向不会改变。当移动至位势垒外时，速度又会回复至原本值。假若，粒子的能量小于位势垒的位势，则在与位势垒 弹性碰撞 之后，这粒子会改变方向，以同样的速率，往回移动。粒子绝对无法存在于位势垒内或越过位势垒。

在量子力学里，粒子的量子行为，是取决于其 波函数 。由于粒子没有被有限位势垒束缚，粒子的能量不是离散能量谱的特殊容许值，而是大于 0 的任意值，因此不需要求算粒子的能量。在这里，主要研究的是粒子的一维散射 。这是一个很有意思的领域。假若，粒子的能量大于位势垒的位势。由于往位势垒传播的波函数，并不是完全地透射过位势垒，仍旧有一部分反射回来。所以，反射的 概率幅 大于 0 ，粒子被反射回来的概率大于 0 。假若，粒子的能量小于位势垒的位势，虽然波函数会呈指数地递减，在位势垒内，概率幅仍旧大于 0 。所以，这粒子存在于位势垒内的概率大于 0。不止这样，概率幅在位势垒外的另一边也大于 0 。假若，位势垒的位势并不大大的超过粒子的能量，位势垒的垒宽也并不很宽，则粒子穿越位势垒的概率会是很显著的，称这效应为 量子隧穿效应 。透射的可能性，称为透射系数；反射的可能性，则称为 反射系数 。