统计套利 Review and Outlook
《Statistical Arbitrage Pairs Trading Strategies, Review and Outlook 》
Author:Drauss Christopher
0. 主要内容:
从5大主流策略,分析统计套利策略的发展历史,各个算法的优缺点及可能改进方案,为学界和业界的研究人提供一个更全更新的视角。
统计套利基础知识,参见:
https://www. zhihu.com/question/3835 97351. 五大类策略
a) 距离法(Distance Approach)
b) 协整法(Cointegration Approach)
c) 时间序列法(Time Series Approach)
d) 随机控制法(Stochastic Control Approach)
e) 其他方法(Machine Learning, Combined Forecasts Approach, Copula Approach, Principal Components Analysis Approach)
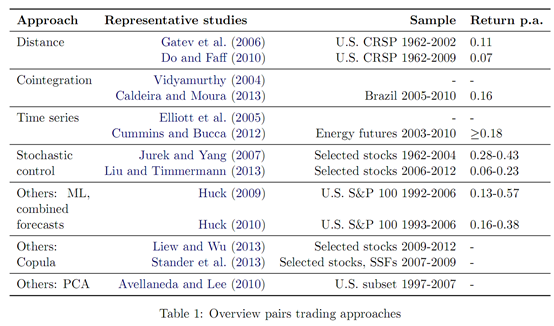
3. 距离法
该类方法经典包含的经典文献如下:
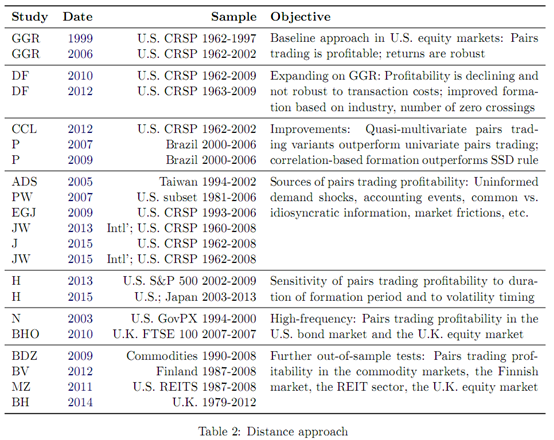
经典方法介绍
其中GGR最为经典。Gatev, E., Goetzmann, W. N., and Rouwenhorst, K. G. (2006). Pair strading: Performance of a relative-value arbitrage rule. Review of Financial Studies, 19(3): 797-827.
以最经典的GGR论文为例(具体是那篇文章,可以参考原文的参考文献),距离法需要一个回溯时间区间,例如选择12个月的时间区间,将价格标准化为序列Pit(期初价格为1),然后计算n只股票n(n-1)/2个两两配对的欧几里得距离(SSD),将SSD最小的配对构建投资组合,当配对资产价格大于回溯期的2个标准差时入场,回复到均值时平仓,6个月后再更换备选配对资产。
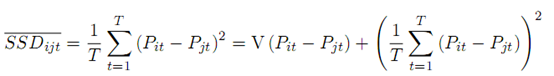
上图为SSD的推导公式,等式右方第一项(记为a)表示价格偏离均值的程度,第二项(记为b)表示均值的漂移程度,如果最小化SSD,则a和b都要最小。但理性投资者希望的是保持均值不漂移的情况使得波动更大,并且稳定,因此要求a大一点,b小一点。但是距离法最终实证结果表明,选出的配对往往是a小b大,因此距离法是一个次优解(suboptimal)。另外GGR的一个缺点是未做协整检验,而高相关性并不意味着协整关系(Alexander 2001),因此其均值回复性不强,有较大的分离风险(价格不收敛)。Do and Faff(2010)发现,GGR文中的方法得到的配对中,32%并不收敛。而协整法得到的配对收敛性更强(Huck 2015)。
方法改进
距离法是否可以改进呢?只做行业内两两股票配对可以提高配对效果(Do and Faff 2010,2012),但忽略了行业间配对的机会,例如供应链两端的买卖双方,消费者-供应链关系暗含了配对的收益机会(Cohen and Frazzini,2008)。在形成期阶段,均值回复经过0的次数越多,样本外均值回复可能越强,能提高距离法的策略收益(Do and Faff 2010,2012),但面临样本内数据挖掘的风险。
Chen et al. (2012) 使用Pearson相关系数作为形成期内相关性的度量,算法为:
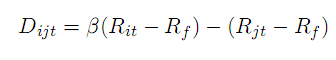
其中Dijt为t时刻股票i收益率Rit偏离股票j收益率Rjt的程度,Rf为无风险收益率。进一步考虑伪多元配对(quasi-multivariate pairs),即股票i与其相关性最高的50只股票配对。未来一个月,根据Dijt的分离度,做多分离度最高组股票,做空分离度最低组股票,保持做多与做空的资金相等。Chen et al. (2012)基于此模型的超额收益达到了1.7%/月,显著高于GGR方法。而其超额收益的来源在于构造50只股票的comver组,如果将50减少到1,则超额收益降低1/3。
Perlin(2007,2009)发现,GGR方法中将价格序列Pit标准化(减均值除方差)后,与Pearson相关系数法的结果相同。另外关于伪多元配对,作者构建了一个与5只票的配对组合:
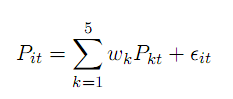
权重w可以用不同的算法得到(等权,OLS,相关性)。结果发现伪多元配对法收益更高且更稳健。
收益来源分析
Andrade et al. (2015) 确认GGR方法在台湾股票市场能获得收益,收益来源为对流动性的补偿。Papadakis and Wysocki (2007) 发现配对股票在盈利公告前发生价格偏离往往会带来较高盈利,而价格分离若发生在非事件驱动时段,则无收益。Chen et al. (2015) 认为收益来自信息的传播延迟。Jacobs and Weber (2013,2015) 发现收益来自信息传递的速度差异,特别是当市场上出现大量非预期信息时,使得投资者的关注点从个股转向市场,造成了个股信息传播速度的差异,表现为股票价格的分离。这一解释适用于全球35个国家的股票市场,并且这一策略是少数的具有alpha的纯多头策略。
提高交易频率
Nath(2013)将GRR策略应用在美国债券上,并且提高了交易频率,尽管获得了不错的夏普和盈亏比,但配对间的分离风险较高。Bowen et al. (2010)运用小时级别数据将配对策略应用到富时100成分股中,但收益很难覆盖交易成本。
4. 协整法
基础知识参见:
https://www. zhihu.com/question/3842 4228
经典文献参考:
Vidyamurthy, G. (2004). Pairs trading: Quantitative methods and analysis. John Wiley & Sons, Hoboken, N.J.
买入1手股票i,卖空r手股票j,配对收益mijt等于
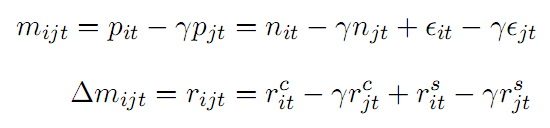
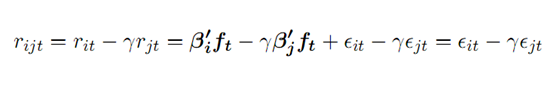
这个算法看似很好,但模型有明显的问题:i)CTM(Common Trend Model)和APT模型能结合吗?ii)APT中的因子怎么定?而美股市场股票收益需要至少30个因子才能解释50%的收益变动(Avellaneda and Lee 2010)。iii)其中参数如何设定,例如测试协整的形成期长度,满足协整条件的最小临界值等等。iv)并且没有做可投资性测试。
策略优化
Lin et al. (2006) 构建了一个优化每笔交易盈亏比的模型:
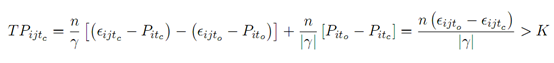
可交易策略
Vidyamurthy (2004)只提出了协整模型的构想,并未用现实金融资产做统计回测模拟。Girma and Paulson(1999),在考虑交易成本后,应用协整模型于原油、汽油、石油期货产品进行套利,年收益达到15%。这一模型的优势来源于其所选标的自身具有生产关系上的强相关性,另外,大豆及其制成品(Simon 1999)、天然气和电价期货(Emery and Liu 2012)这两个配对交易也能获取超额收益,但金银间无套利机会(Wahab and Cohn 1994)。股票上的协整模型产生了33%的年化收益(Hong and Susmel 2003),但其收益部分来自汇率升值(Broumandi and Reuber 2012)。Dunis et al.(2012)将协整法推进到了股票“更高频”交易中,标的选择为欧洲斯托克50成分股,配对股票两两之间的资金配比使用卡尔曼滤波进行估计,但该模型忽略了例如配对公司的杠杆比例差异带来的分离风险。Caldeira and Moura(2013)在巴西股票市场做了测试,其使用Engle-Granger两步法及Johansen法则检验协整关系,但其选择配对股票的依据是样本内套利收益的夏普率而不是相关系数等。这一模型也有其问题,即Engle-Granger两步法及Johansen法则具有相关性,其并没有起到两重检验保护的效果。Gutierrez and Tse(2011)使用3只自来水公司股票做协整检验,发现收益来自于Granger-follower,而不是Granger-leader(编者注:不太清楚这两个单词的含义,是否有朋友能帮忙解释下)。重点来了,AH股市场存在协整套利机会(Li et al. 2014)!
多元变量协整配对
被动指数型(基于某个指数):Dunis and Ho(2005)在欧洲斯托克50中选出5-20只协整关系较强的股票,发现其收益跑过指数。
主动统计型(更广泛的数据挖掘协整关系):Galenko et al.(2012)挖掘长期更稳健的协整关系,但过于依赖样本内信息,参数设置苛刻。
多策略:Burgess(1999)将协整法与神经网络、遗传算法相结合,该论文是唯一在统计套利中尝试这类算法结合的文章,因此非常有吸引力。
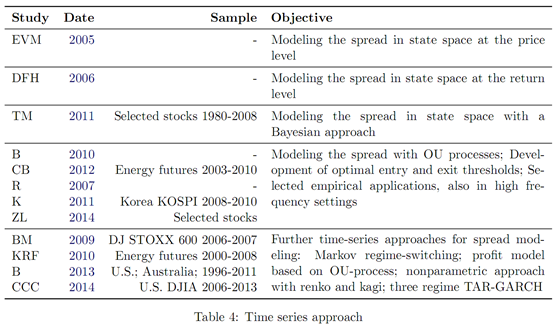
5. 时间序列法
标志性经典文献:Elliott, R.J., Van Der Hoek*, John, and Malcolm, W.P. (2005). Pairstrading. Quantitative Finance, 5(3): 271-276.
Elliott et al. (2005)将价差定义为均值回归特性的马尔科夫链,并伴随有高斯噪声。假设一个状态变量x满足均值回复特征:
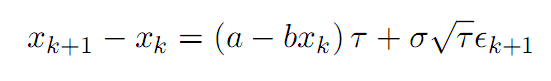
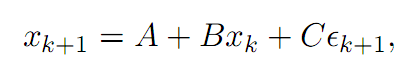
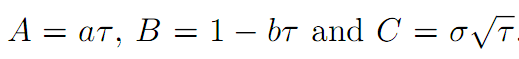
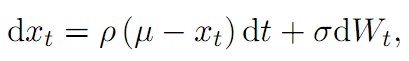
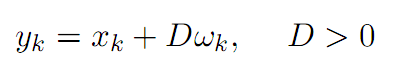
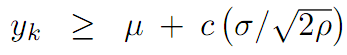
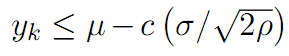
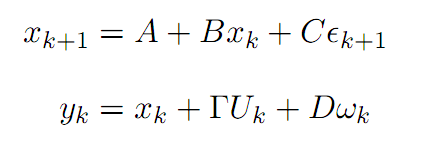
Triantafyllopoulos and Montana(2011)对上一模型在两方面做了改进,一是提高参数的时序特征,二是用贝叶斯过程估计参数,显著降低了大样本数据情况下(例如高频)估算参数的时间。
Ornstein-Uhlenbeck过程的应用
Bertram(2010)模拟了配对交易入场到出场的时长T1和出场到下一次入场的时长T2:
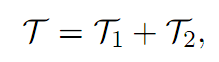
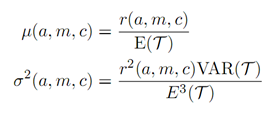
6. 随机控制法
标志性经典文献:Jurek, J. W. and Yang, H. (2007). Dynamic portfolio selection in arbitrage. Working paper, Harvard University.
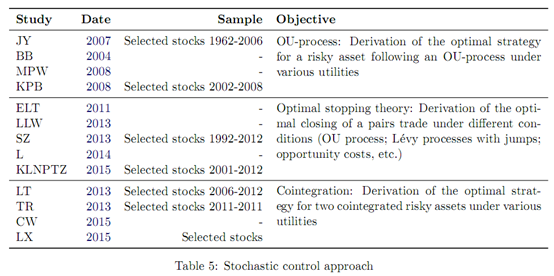
Jurek and Yang(2007)假设投资者在最优化递归Epstein-Zin效用函数的基础上,动态配置套利模型和无风险资产,应用随机控制理论,作者推导出Hamilton-Jacobi-Bellmann(HJB)方程,并求出闭合解。该文的贡献在于,第一,利用OU过程模拟不确定性的套利机会,而传统方法多采用布朗桥,第二,构建了两套效用函数,短期套利投机需求和套保需求,第三,符合静态边界条件,即价差在静态边界内部时投机者不参与交易,第四,在高均值回复条件下,策略收益显著高于GGR距离法。但问题在于,低均值回复特征下、度量误差存在的情况下,收益不够显著,日度调仓换手率过高,一旦考虑交易费用则显著降低收益。Ekstrometal. (2011), Larssonetal. (2013), Song and Zhang (2013), Lindberg (2014) and Kuoetal. (2015) 考虑在加入止损条件下的策略优化。
误差纠正模型
Liu and Timmermann (2013)放开delta中性约束,模拟价格变化为布朗运动:
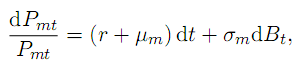
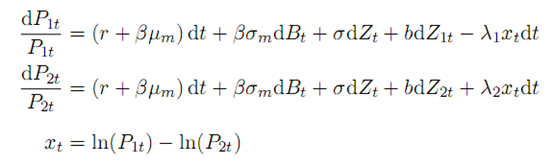
7. 其他方法
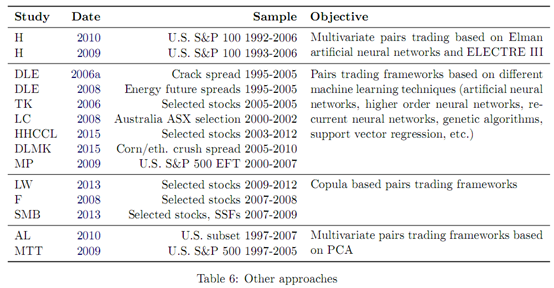
Huck, N. (2009). Pairs selection and outranking: An application to the S&P 100 index. European Journal of Operational Research, 196(2): 819-825.
Huck, N. (2010). Pairs trading and outranking: The multi-step-ahead forecasting case. European Journal of Operational Research, 207(3): 1702-1716.
Huck是唯一应用这两种方法于统计套利并发表文章作者。其模型的基本方法步骤为,预测,排序,交易。在预测阶段,运用神经网络算法预测每只股票的下一周收益;排序阶段,构建了多标准决策方法(MCDM),对每只股票的排序基于多个标准评分,不同的标准评分可以用等权组合。该模型是一个非均衡模型,周度超额收益高达0.8%,但问题在于存在生存者偏差,MCDM的设计方式过于复杂,并且没有一个简单的比较基准。除此之外,有少量的文章涉及到了机器学习算法在统计套利中的应用,但策略涉及不够完善或者数据选取的股票不具有代表性。
Copula方法
重要的文献包括了3篇,Ferreira(2008),Liew and Wu(2013),Stander et al.(2013)。Copula方法的演算方法为,在形成期内计算配对的相关系数或协整标准,然后计算配对股票收益序列的边际分布函数。对于收益边际分布函数,Stander et al.(2013)讨论了参数和非参数法两种方法来估计边际分布,Ferreira(2008)和Liew and Wu(2013)则偏向于拟合参数分布函数。在得到边际分布函数后,即可确定合适的copula函数。Ferreira(2008)仅使用了一个Copula函数,参数来自经典最大似然估计。Stander et al.(2013)基于22个阿基米德copula,运用Kolmogorov-Smirnov拟合度测试选出最佳copula。Liew and Wu(2013)则是从5个金融领域常见的copula中选择。3篇文献的交易策略类似,均是使用选出的copula函数C(u,v)计算条件边际分布:
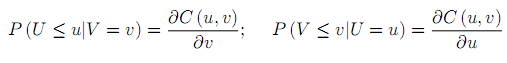
主成分分析法
Avellaneda and Lee(2010)将股票收益分解为系统性(共同)和异质收益两部分。第一种方法只考虑一个系统性因子,即行业收益:
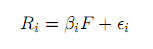
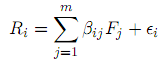
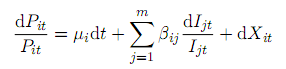
8. 总结
距离法
优势:算法简介;避免数据挖掘;伪多元配对法优于单配对法;在传统风险因子上无暴露,且适用于不同类别的资产;
缺陷:SSD筛选标准使得配对的方差变动过小,降低了收益的空间,而Pearson标准相对更佳;
改进方向:改进筛选标准,例如结合协整法可以选出更加稳定的配对;全球各类资产的套利收益可能找到共同的解释因素,类似于Asness et al.(2013)发现价值和动量解释全球各类资产收益。
协整法
优势:在确定配对的均衡特性上,使用的计量方法较距离法更加严格和合理;
缺陷:目前的实证研究仅基于少数股票;
改进方向:Vidyamurthy(2004)提出的启发式数据检验方法值得进一步的探索;多元统计套利法也值得更多研究
时序法
优势:基于时间序列的动态交易法则具有可操作性;
改进方向:讨论距离法,协整法,和时序法之间的关系会比较有意思;并且时序法的交易算法部分也有改进的空间;
随机控制法
优势:较距离法对收益的获取有提升;
改进方向:使用协整法确定配对,时序法确定入场时机,随机控制法进行仓位的控制,三种方法可以发挥各自的优势。
