配色和色度图

来源：雪球App，作者： 书生剑客，（https://xueqiu.com/3993902801/181048173）

三基色的选择不是唯一的。由于红、绿、蓝相加三基色能配出的色域较广，品种较多，所以人们愿意选用红、绿、蓝相加三基色。原则上，只要三种颜色的任一种都不能被其余两种相加配出，那么这三种颜色就是一组三基色。

需要说明的是，任何实际的三基色，即使较好的红、绿、蓝，也不能配出自然界所有的一切颜色。增加基色总数，才能扩大配色的色域。但是基色过多，使用上不方便。事实上，红、绿、蓝三种基色已基本满足了实际上的需要。三原色原理提示我们一种表示色的途径。假设我们把红、绿和蓝三种颜色，用R、G和B来标记，于是，某一种颜色就可以由这三种颜色的一定数量(彩色量)制成。比如，由颜色R的数量a, 颜色G的数量b和颜色B的数量c制成新的颜色F，则

F=aR+bG+cB

上式中，a, b和c称为三色系数。显然，选用不同的三基色，去标定(配成)同一颜色将有不同的三色系数。由此选用不同的三基色将产生不同的三色系统。国际照明委员会规定，波长为700nm的红光为红基色光，波长为546.1nm的绿光为绿基色光，波长为435.8nm的蓝光为蓝基色光。我们可以通过以下的配色实验来验证颜色的合成。配色实验的任务是求出合成某一种彩色光所需的三种基色光的比例：

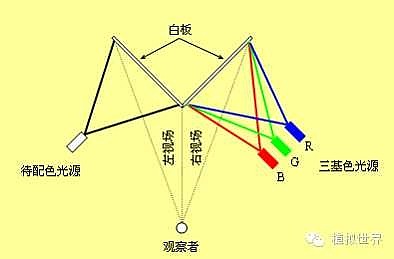
它是由两块相互垂直的白板组成的，白板对任何波长的光的反射率都接近100％，这样将人眼的视野分成二等分。待配色位于一边，三种基色位于另一边。三种基色光的光通量是可调节的，从而可改变三者的混合比例。由于两块白板形成的夹角把人眼的视野分成二等分，让视场两边的光分别投射到视场中的两块白板上，通过调节三种基色的混合比例，就可使两边的彩色一致，这时，在整个视场中，人眼只看到一种彩色。如图，白板的左半部分投射待配的彩色光，右半部分投射红、绿、蓝三基色光。调节三基色光的光通量使白板左、右部分的彩色光完全相同，这时调节器刻度所示的数值就分别是混配F色光所需的红、绿、蓝的比例。

若待配色为标准白光，实验表明，要用上述三种基色混出等能白光，三种基色光的光通量必须满足一定的比例：

|Φ(R)|:| Φ(G)|:| Φ(B)|=1 : 4.5907 : 0.0601

由于标准白光的三种基色光的光通量比例有效数字是4位小数，计算起来不方便，因此，国际上规定了基色单位。即，1个红基色单位：1[R]—光通量为1lm的红光；1个绿基色单位：1[G]—光通量为4.5907lm的绿光；1个蓝基色单位：1[B]—光通量为0.0601lm的蓝光。

根据上述结论，我们将上述比例构成的三基色值规定为单位刺激值，即[R]，[G]，[B]，称为三色单位。这样，对于配色方程F＝R[R]＋G[G]＋B[B]，当R、G、B系数都等于1时，可以混出白光。此时，我们可称为，三基色光等量混合混为白光。

等能白光是光谱辐射密度在可见光范围内不变的一种光，这种光自然界中是不存在的，实验室可近似配制出来。对于标准白光可表示为下式，总光通量为Φ（F）＝1+ 4.5907 + 0.0601 = 5.6508 lw；

F(E白)=1[R]+1[G]+1[B]

若三基色光同时增大到原来的K倍，则混配之后仍然得到白光，只不过其光通量也增大到原来的K倍。

E'白=K[R]+K[G]+K[B]

任意给定的彩色光，配色方程F＝R[R]＋G[G]＋B[B]，R、G、B分别为红、绿、蓝基色单位数，称为三色系数。三个色系数的比例决定了所配彩色光的色度；而R[R]、G[G]、B[B]分别代表彩色量F中所含三基色的光通量成分，又称为彩色分量（三色分量）；它们的数值之和则决定了所配彩色光的总的光通量。该色的光通量为：Φ（F）＝（R + 4.5907*G+ 0.0601*B）光瓦＝680*（R + 4.5907G+ 0.0601B）流明。

由此我们可以得到关于配色的几个结论：

当三色系数同时扩大或缩小若干倍时，所混出来的彩色的色度不变，而仅仅是亮度发生改变。这说明，决定一个彩色的色度，不是三色系数本身，而是三色系数的比例。而三色系数的比例只需用两个量来表示就够了。故虽然彩色系统是一个三维系统，但是色度系统却是两维系统。当三色系数相等时，即R＝G＝B时，一定表示等能白光。当R＝G＝B＝1时，表示5.6508光瓦的等能白光。当若干个彩色相混时，混合色的色系数为各混合分量的色系数之和。例如有两个彩色：F1＝R1[R]＋G1[G]＋B1[B]，F2＝R2[R]＋G2[G]＋B2[B]。如果将F1和F2相混，则混合色F(1+2)为：F(1+2)＝ F1＋ F2＝（R1 ＋ R2）*[R]＋（G1 ＋ G2）*[G]＋（B1 ＋ B2）*[B]，这一表达式称为彩色合成方程式。

在配色实验中，要配出某一待配色，无论怎样改变三种基色的比例都不能使两边的彩色感觉相同，这时，要将三种基色中的一种基色光移到待配色一侧，待配色与移过来的这种基色所混合的色与另一侧没有移动的两种基色合成的色光完全一致，所移的基色对应的色系数就用负值表示。例如用红（R）、绿（G）、蓝（B）匹配光谱黄色，需把蓝色（B）加到待配色黄色（F）一边再进行匹配(F)+B(B)=R(R)+G(G)，则F＝R(R) + G(G)- B(B);

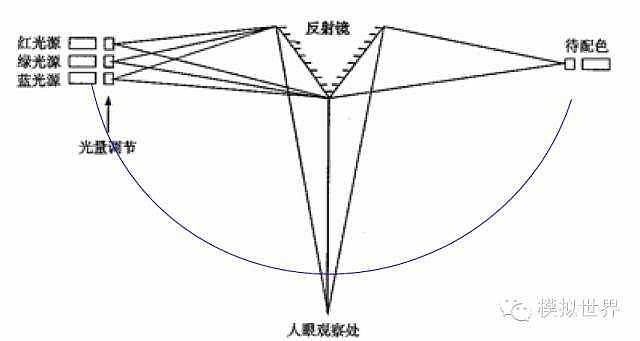
匹配某种颜色所需的三原色的量称做该颜色的三刺激值。颜色方程F＝R[R]＋G[G]＋B[B]中的R、G、B 就是三刺激值。三刺激值不是用物理单位，而是用色度学单位来度量。对于既定的三原色，每种颜色的三刺激值是唯一的，至此，我们可以使用R、G、B三个系数值来定量的表述一个颜色。由于颜色仅取决于R、G、B的比例，而非它们的大小。所以我们可以用两个量来准确的表述一种颜色：

r=R/(R+G+B); g=G/(R+G+B) b =B/(R+G+B);  r+g+b =1;

r,g,b称为相对色系数，也称色度坐标。由于r+g+b=1,色度可唯一地由r、g、b中的两个就可以明确地表示。因此各种彩色的色度可以采用二维表示法。此时，我们将用r为横坐标、g为纵坐标，r、g就称为色度坐标。由r和g所决定的平面上的点均和某种颜色相对应，这样一个能表示颜色的平面，称做色度图。现将380nm到780nm的所有纯色光进行配色实验，求得其色度坐标，并标注于r、g坐标系中，得到RGB色度图。

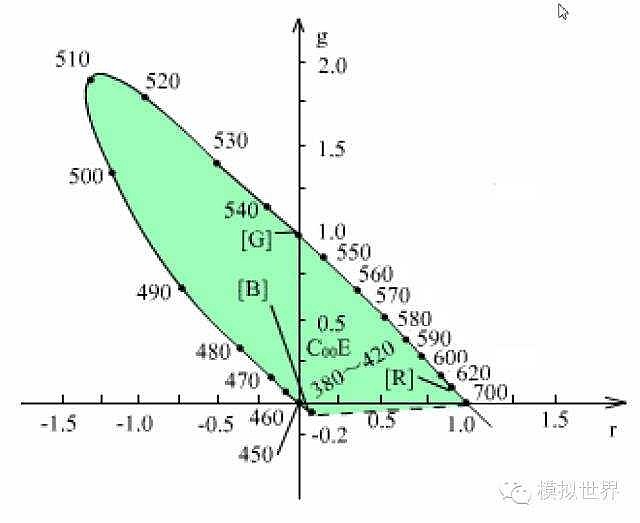
RGB色度图的进一步讨论：

所有亮度不同但色度相同的彩色，在RGB色度图中的坐标都相同。在波长380nm～420nm和700nm~780nm范围内，人眼已经感觉不到色度的不同了，而只能感到亮度的不同。故它们处于同一坐标点上。等能白光的色度坐标为r＝l/3，g＝l/3。这是因为对于等能白光来说，有R＝G＝B。如果有两个不同的彩色F1和F2，它们在色度图上对应两个坐标点（rl、g1）和（r2、g2）。如果将F1和F2相混则混合色F（1＋2）的坐标点一定处于由F1和F2所决定的直线上，且一定位于F1和F2之间。

我们将图中的两个端点用直线连接起来，则原本开口的谱色轨迹成为封闭曲线了。这条直线上的任何点所代表的彩色，都可以看成是谱色轨迹的两个端点的谱色光混色的结果。由于靠近780nm的谱色为红色光，靠近380nm的谱色为蓝色光，则混合色必为紫色。只不过，如果靠近780urn处，则混合色为偏红的紫色；如果靠近380urn处，则混合色为偏蓝的紫色。所以，这条直线称为紫色直线。

从理论上讲，三基色是有很多种的，只要它们相互独立。但是用不同的三色系统去讨论颜色规律问题，需要换算，极不方便。而RGB计色系统采用物理三基色，因而物理意义清楚，但使用起来却很不方便。所以我们希望有一种三基色值，可以实现一些特殊的要求，比如用它们配色得到的三色系数均为正值；但该三基色也必须满足三基色选取的一般规则。CIE设法选取了三个基色（不存在的虚拟色），构成了新的色度坐标系，使得所有的颜色全部是正颜色系数。这些颜色系数与RGB色度坐标系中的颜色系数有唯一的数学转换关系。CIE将该色度坐标系制定为色度标准，即XYZ计色制，又称标准计色制。

在XYZ计色系统中，基色XYZ只是假想的三基色，但是借助它们来计算各种实际颜色却十分方便。选择XYZ计色系统的目的就是为了克服RGB计色系统的缺点，因此，在确定基色量[X]、[Y]、[Z]时有一些特定的要求：

用配色方程F＝X[X]＋Y[Y]＋Z[Z]配色时，三个色系数均应为正值；

为便于计算，合成彩色光F的亮度应仅由Y[Y]项的系数Y决定，与X、Z值无关。且1[Y]=1lw，不过，合成光F的色度仍由X、Y、Z的比例关系决定。 X＝Y＝Z时，仍代表等能白光；

[X]、[Z]项不提供亮度， [X]、[Z]必然在零光通量的轨迹上（零亮度线上）；

因为X、Y、Z为正值，所以舌形曲线内所包含的各种颜色的坐标都应落在以[X]、[Y]、[Z]三点构成的三角形内。需求另二边；

XY连线方程：过700nm、640nm的直线延长线；

YZ连线方程：舌形曲线左侧一条直线，CIE规定：略离开504nm点的切线的平行线。

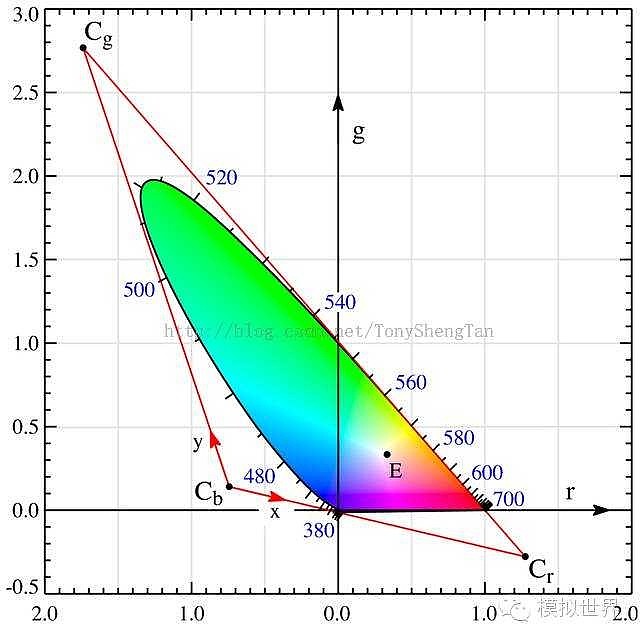
由此，可以的到基色单位量[X]、[Y]、[Z]与[R]、[G]、[B]的关系：

[X] =  0.4185[R] - 0.0912[G] + 0.0009[B]

[Y] = - 0.1587[R] + 0.2524[G] -0.0025[B]

[Z] = - 0.0828[R] + 0.0157[G] +0.1786[B]

求解基色单位量[X]、[Y]、[Z]与[R]、[G]、[B]的关系的过程如下：

而色系数X、Y、Z与R、G、B的关系为：

X = 2.7689R + 1.7518G + 1.1302B

Y = 1.0000R + 4.5907G + 0.0601B

Z = 0.0000R + 0.0565G + 5.5943B

或者

对于XYZ 制中彩色表示式的配色方程F＝X[X]＋Y[Y]＋Z[Z] ＝(X＋Y＋Z) * (x[X]＋y[Y]＋z[Z]);  x=X/( X＋Y＋Z); y = Y/( X＋Y＋Z); Z = Z/( X＋Y＋Z);  x+y+z=1;

则色度可唯一地由x、y、z中的两个就可以明确地表示。因此各种彩色的色度可以采用二维表示法。此时，我们将用x为横坐标、y为纵坐标得到如下XYZ色度图：

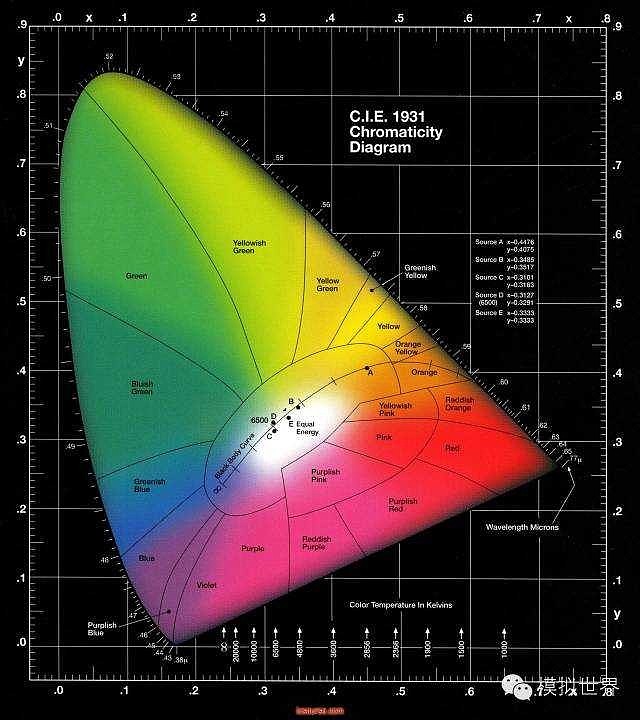
这就是CIE1931标准色度学系统的由来，它是1931年在CIE第八次会议上提出和推荐的，包括1931CIE-RGB和1931CIE-XYZ两个系统，即上述RGB色度图和XYZ色度图；

现代色度学采用国际照明委员会(简称CIE)所规定的一套颜色测量原理、数据和计算方法，称为CIE标准色度学系统。在这个系统中，CIE1931XYZ 色度图，占有相当重要的地位。它明确表示了颜色视觉的基本规律以及颜色混合的一般规律，是色度学的实际应用工具。很多有关色度学的计算和延伸都是由此出发的。

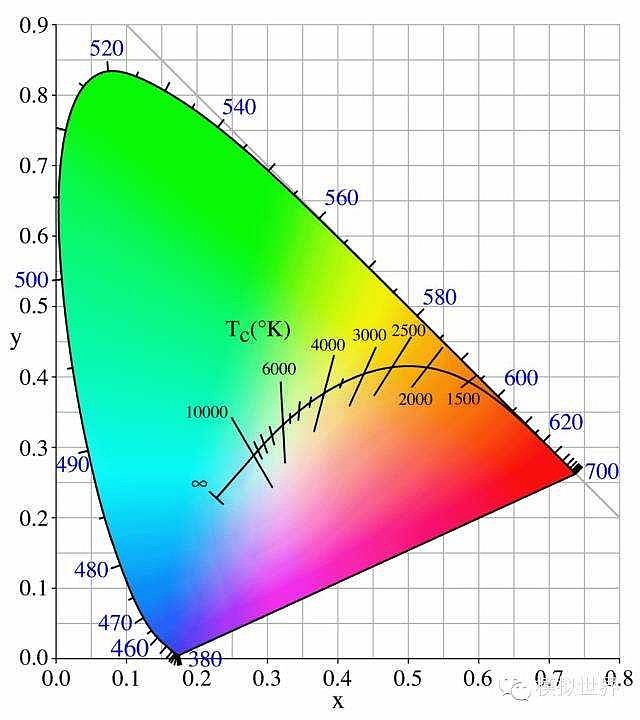
当绝对黑体的温度由低到高连续变化时，其色度坐标将画出一条曲线,不同色温的光源可用轨迹上的某些点来表示，如下图：

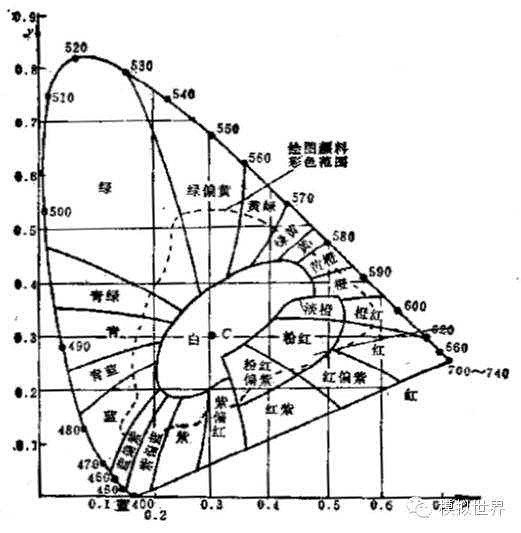
舌形曲线是由各种波长谱色光的坐标构成，曲线上的点可以用波长标记，也可用色度坐标表示。曲线内部各点对应复合光，只能用色度坐标表示。根据不同坐标处颜色的不同，可以将曲线所包围的面积大致分成若干小区，每个区域都标出该处的颜色名称。图中虚线所示采用相减混色法的绘图颜料所描绘的彩色范围。

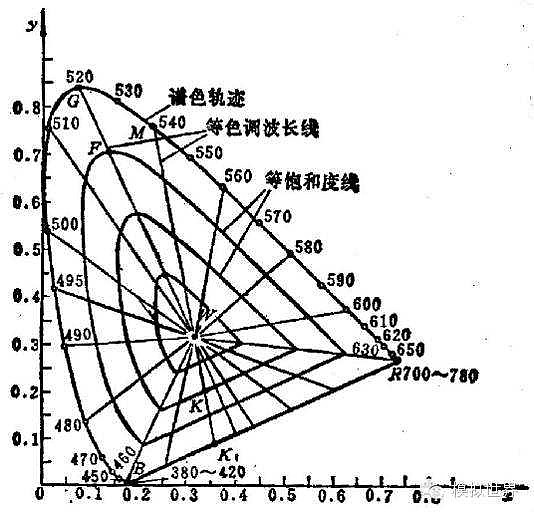
等色调波长线：由 W点（等能白光）引向谱色轨迹的直线均为等色调波长线，其与谱色轨迹的交点所对应的波长，即为该直线上各点彩色的色调波长。

等饱和度线：由色调波长不同而饱和度相同的各点轨迹。

LUV色彩空间全称CIE 1976(L*,u*,v*)，（也作CIELUV色彩空间），L*表示物体亮度，u*和v*是色度。于1976年由国际照明委员会CIE提出，由CIEXYZ空间经简单变换得到，具视觉统一性。