在线工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 3D数字孪生场景编辑器

用于 PyTorch 中时间序列预测的 LSTM

• 什么是 LSTM 以及它们有何不同
• 如何开发用于时间序列预测的 LSTM 网络
• 如何训练 LSTM 网络

概述

这篇文章分为三个部分;他们是

• LSTM 网络概述
• 用于时间序列预测的 LSTM
• 培训和验证您的 LSTM 网络

LSTM 网络概述

LSTM 单元是一个构建块，可用于构建更大的神经网络。虽然常见的构建块（如全连接层）只是权重张量和输入的矩阵乘法以产生输出张量，但 LSTM 模块要复杂得多。

典型的 LSTM 单元如下所示

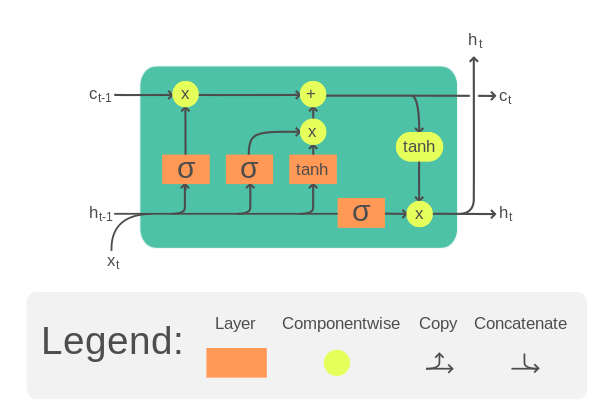
LSTM 单元。插图来自维基百科。

它需要输入张量�以及单元格存储器�和隐藏状态ℎ的一个时间步长。单元存储器和隐藏状态可以在开始时初始化为零。然后在 LSTM 单元中，�、�和ℎ将乘以单独的权重张量，并多次传递一些激活函数。结果是更新的单元内存和隐藏状态。这些更新的�和ℎ将用于输入张量的 **下一个时间步长**。在最后一个时间步结束之前，LSTM 单元的输出将是其单元内存和隐藏状态。

具体来说，一个 LSTM 单元的方程如下：

$$
\begin{aligned}f_t &= \sigma_g（W_{f} x_t + U_{f} h_{t-1} + b_f） \\ i_t &= \sigma_g（W_{i} x_t + U_{i} h_{t-1} + b_i） \\ o_t &= \sigma_g（W_{o} x_t + U_{o} h_{t-1} + b_o） \\ \tilde{c}_t &= \sigma_c（W_{c} x_t + U_{c} h_{t-1} + b_c） \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tilde{C}_t \\ h_t &= o_t \odot \sigma_h（c_t） \end{aligned}
$$

其中 $W$、$U$、$b$ 是 LSTM 单元的可训练参数。上面的每个方程都是针对每个时间步长计算的，因此下标为 $t$。这些可训练参数将哪里所有时间步长。共享参数的这种性质为 LSTM 带来了内存功率。

请注意，以上只是 LSTM 的一种设计。文献中有多种变体。

由于 LSTM 单元期望输入 $x$ 以多个时间步长的形式出现，因此每个输入样本都应该是一个 2D 张量：一个维度表示时间，另一个维度表示特征。LSTM 单元的功率取决于隐藏状态或单元存储器的大小，隐藏状态或单元存储器的维度通常大于输入中的特征数。

想开始使用 PyTorch 进行深度学习吗？

立即参加我的免费电子邮件速成课程（带有示例代码）。

单击以注册并获得该课程的免费PDF电子书版本。

下载您的免费迷你课程

用于时间序列预测的 LSTM

让我们通过一个例子看看如何使用 LSTM 来构建时间序列预测神经网络。

您将在这篇文章中看到的问题是国际航空公司乘客预测问题。这是一个问题，给定一年和一个月，任务是以 1，000 为单位预测国际航空公司乘客的数量。数据范围从 1949 年 1960 月到 12 年 144 月，即 <> 年，共 <> 次观测。

这是一个回归问题。也就是说，给定最近几个月的乘客人数（以 1，000 为单位），下个月的乘客人数是多少。数据集只有一个要素：乘客数量。

让我们从读取数据开始。数据可以在这里下载。

将此文件保存为本地目录中的内容。 airline-passengers.csv

下面是文件前几行的示例：

数据有两列，即月份和乘客人数。由于数据是按时间顺序排列的，因此您可以仅采用乘客数量来创建单要素时间序列。下面您将使用 pandas 库读取 CSV 文件并将其转换为 2D numpy 数组，然后使用 matplotlib 绘制它：

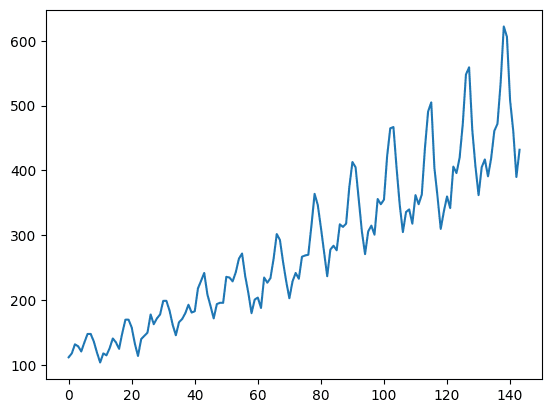
此时间序列有 144 个时间步长。从图中可以看出，有上升趋势。数据集中也有一些周期性，对应于北半球的暑假期间。通常，时间序列应该被“去趋势化”以去除线性趋势分量，并在处理之前进行归一化。为简单起见，本项目中跳过了这些内容。

为了展示模型的预测能力，将时间序列分为训练集和测试集。与其他数据集不同，通常拆分时序数据而不进行随机排序。也就是说，训练集是时间序列的前半部分，其余部分将用作测试集。这可以在 numpy 数组上轻松完成：

更复杂的问题是您希望网络如何预测时间序列。通常，时间序列预测是在窗口上完成的。也就是说，给定从时间 $t-w$ 到时间 $t$ 的数据，要求您预测时间 $t+1$（或更深的未来）。窗口 $w$ 的大小决定了您在进行预测时可以查看的数据量。这也称为更复杂的问题是您希望网络如何预测时间序列。通常，时间序列预测是在窗口上完成的。也就是说，给定时间数据。

在足够长的时间序列上，可以创建多个重叠窗口。创建函数从时间序列生成固定窗口的数据集很方便。由于数据将在 PyTorch 模型中使用，因此输出数据集应位于 PyTorch 张量中：

此函数旨在对时间序列应用窗口。假设它预测到不久的将来的一个时间步。它旨在将时间序列转换为维度张量（窗口样本、时间步长、特征）。$L$ 时间步长的时间序列可以产生大约 $L$ 的窗口（因为只要窗口不超出时间序列的边界，窗口就可以从任何时间步开始）。在一个窗口中，有多个连续的时间步长值。在每个时间步长中，可以有多个要素。在此数据集中，只有一个。

有意使“特征”和“目标”具有相同的形状：对于三个时间步长的窗口，“特征”是从 $t$ 到 $t+2$ 的时间序列，目标是从 $t+1$ 到 $t+3$ 的时间序列。我们感兴趣的是 $t+3$，但 $t+1$ 到 $t+2$ 的信息在训练中很有用。

请注意，输入时间序列是 2D 数组，函数的输出将是 3D 张量。让我们尝试使用 .您可以按如下方式验证输出张量的形状： create_dataset()lookback=1

您应该看到：

现在，您可以构建 LSTM 模型来预测时间序列。有了 ，可以肯定的是，对于无法预测的线索太少，准确性将不利。但这是一个很好的例子来演示 LSTM 模型的结构。 lookback=1

该模型被创建为一个类，其中使用 LSTM 层和全连接层。

的输出是一个元组。第一个元素是生成的隐藏状态，每个时间步长对应一个。第二个元素是 LSTM 单元的内存和隐藏状态，此处不使用。 nn.LSTM()

LSTM 图层是使用选项创建的，因为您准备的张量位于 （窗口样本、时间步长、特征） 的维度中，并且通过在第一维度上采样来创建批处理。 batch_first=True

隐藏状态的输出由全连接层进一步处理，以产生单个回归结果。由于 LSTM 的输出是每个输入时间步长一个，因此您可以选择仅选择最后一个时间步的输出，您应该具有：

模型的输出将是下一个时间步长的预测。但在这里，全连接层应用于每个时间步。在此设计中，应仅从模型输出中提取最后一个时间步长作为预测。但是，在这种情况下，窗口为1，这两种方法没有区别。

培训和验证您的 LSTM 网络

因为它是一个回归问题，所以选择MSE作为损失函数，由Adam优化器最小化。在下面的代码中，PyTorch 张量被组合成一个数据集，使用 和 批处理训练由 .在训练集和测试集上，每 100 个 epoch 评估一次模型性能： torch.utils.data.TensorDataset()DataLoader

由于数据集很小，因此应该训练模型足够长的时间以了解模式。在这 2000 个训练的 epoch 中，您应该看到训练集和测试集上的 RMSE 都在减少：

预计测试集的RMSE将大一个数量级。RMSE 为 100 表示预测和实际目标值平均为 100（即此数据集中的 100，000 名乘客）。

为了更好地理解预测质量，您确实可以使用 matplotlib 绘制输出，如下所示：

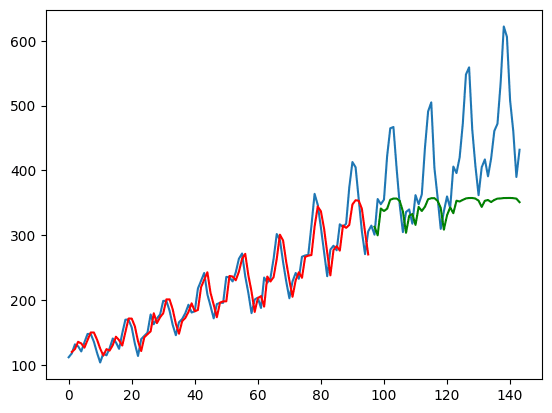
从上面可以看出，您将模型的输出作为，但仅提取最后一个时间步长的数据作为 。这是图表上绘制的内容。 y_predy_pred[:, -1, :]

训练集以红色绘制，而测试集以绿色绘制。蓝色曲线是实际数据的样子。您可以看到模型可以很好地适应训练集，但在测试集上不是很好。

捆绑在一起，下面是完整的代码，只是这次参数设置为 4： lookback

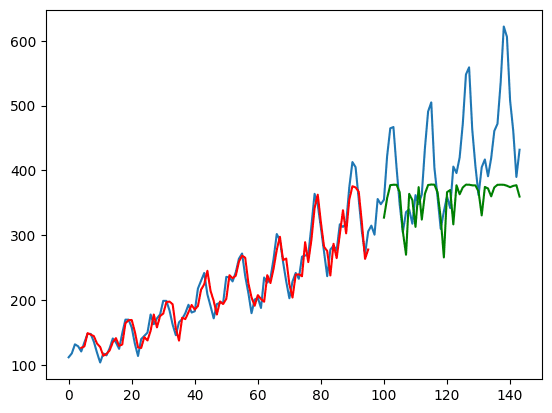
运行上面的代码将产生下面的图。从打印的 RMSE 测量值和绘图中，您可以注意到模型现在可以在测试集上做得更好。

这也是函数以这种方式设计的原因：当模型被赋予一个$t$到$t+3$（as）的时间序列时，它的输出是$t+1$到$t+4$的预测。但是，输入中也知道$t+1$到$t+3$。通过在损失函数中使用这些，有效地为模型提供了更多用于训练的线索。这种设计并不总是合适的，但你可以看到它在这个特定的例子中很有帮助。 create_dataset()lookback=4

由 3D建模学习工作室 翻译整理，转载请注明出处！