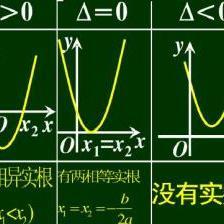
|
|
判别式
知乎十年新知答主
对于实系数的一元二次方程，你的命题是成立的。 如果一元二次方程的系数不全是实数，就可以出现一个实根和一个虚根的情况。 譬如： [公式] ，因式分解可得 [公式] ，解得 [公式] ， [公式] 。易知，该方程的判别式 [公式] 。由于只有实数之间才能比较大小，实数和虚数、虚数和虚数都不能比较大小。此时，讨论 [公式] 的正负号已经没…
仔细想了想，我觉得题主的疑问应该来自于一元三次方程的求根公式， [图片] 当 [公式] ，求根公式中 [公式] 会出现虚数 [公式] ，为什么反而得到的是三个实数？而且这个根式解中的 [公式] 在根式情形下，几乎是无法消除的。其实百度中有解释，求根公式第一个解是实数还是比较好理解，有前后两个三次方根部分相加，这两个部分三次根号下的表达式是共轭的，根据复…
只求青山依在
首先一元二次方程的一般形式为 [公式] 有重根，意味着函数图像与x轴只有一个交点 [公式] ，同时这个点满足两个关系： [公式] 代入 [公式] ，得 [公式]
九年级数学21.2解一元二次方程系列4
配方法解一元二次方程 一元二次方程根的判别式 公式法解一元二次方程 因式分解法解一元二次方程 一元二次方程根与系数的关系 运用公式法解一元二次方程时出错 解方程时方程两边同时除以含未知数的相同因式而失根 …
高等代数：对称多项式的性质及多项式的判别式
对称多项式是多元多项式中特殊的一类，它的每一个变量在多项式中的地位都是对称的。对称多项式的定义如下： [图片] 一、初等对称多项式与对称多项式基本定理 初等对称多项式指在多元多项式环 [公式] 中，含有项 [公式] 的项数最小的n元对称多项式.容易看出： [公式]
要保障睡眠质量。
首先，纠正一下题主的问题里的小瑕疵. 函数没有根，方程才有根.题主可能是想说函数的零点吧 这里， [公式] 表示的是一元二次方程 [公式] 的判别式，次数大于等于2的方程都有判别式，方程是几次，根（或者说“解”）就有几个.对于2次方程，根永远都是两个，根的个数是不会变的.判别式判断的是根的特征，不是根的个数.对于一元二次方程判别式，严谨的说法应是： [公式] [公式]
先考虑一个二次方程 [公式] [图片] 我们可以通过观察极值点的纵坐标来判断根的情况 极值点的纵坐标为 [公式] 显然极值点的纵坐标分为大于零、等于0、小于零三种情况，分别对应没有实根、两个相等实根、两个不等实根的情况 比如没有实根的情况 [公式] 接下来用这种方法考…
九年级数学21.2解一元二次方程系列1
配方法解一元二次方程
一元二次方程根的判别式
公式法解一元二次方程