吴文俊：不朽的数学人生，照耀人工智能发展之路

祖国的光荣榜上， 闪耀着科技之光 。居功至伟彪炳史册，榜样力量亦指引后人。

9月17日，全国人大常委会关于授予国家勋章和国家荣誉称号的决定获表决通过，共有42人获得国家勋章、国家荣誉称号。其中， 中国人工智能学会原名誉理事长、中国科学院院士吴文俊获“人民科学家”国家荣誉称号 。

吴文俊院士曾任中国科学院数学与系统科学研究院研究员，中国科学院院士，中国人工智能学会原名誉理事长。他对数学的核心领域拓扑学作出重大贡献，开创了数学机械化新领域，对国际数学与人工智能研究影响深远。他用算法的观点对中国古算作了分析，同时提出用计算机自动证明几何定理的有效方法，在国际上被称为“吴方法”， 曾荣获国家最高科学技术奖 。

值得一提的是， 被誉为“中国智能科学技术最高奖”的“吴文俊人工智能科学技术奖”，正是由吴院士命名 。该奖项由中国人工智能学会发起主办，自2011年设立以来，每年颁发一次，对获奖者颁发100万奖金，2018年还首度设立“吴文俊人工智能杰出贡献奖”中国从事智能科学技术领域研发、生产、应用、推广的企业和机构，从事智能科学技术教学与研究的高校与科研院所或院士专家，均可通过中国人工智能学会官网平台申报该奖。

吴文俊不朽的数学人生

“他的成果都是独出蹊径，不袭前人，富创造性。”“这是一个十分杰出的数学家！” 这是陈省身对学生吴文俊的评价。

每一个数学精英， 都会因自己获得哪怕是其中的一个奖项而荣耀一生 。吴文俊的数学人生早已荣誉等身：首届国家最高科技奖（2000）、首届国家自然科学一等奖（1956）、有东方诺贝尔奖之称的邵逸夫数学奖（2006）、国际自动推理最高奖Herbrand自动推理杰出成就奖（1997）。但翻开吴文俊的历史篇章，我们会发现，他对数学曾有一个从无偏爱到略有兴趣，又失去兴趣，再到终生热爱的过程。

初中时， 吴文俊其实对数学并无偏爱 ，成绩也不突出，到高中逐渐对数学及物理，特别是几何与力学产生学习的兴趣。1936年他中学毕业，并没有专攻数学的想法，而且家庭供他上大学也存在困难。好在当时他就读的中学设立了3个奖学金名额，其中一个便指定给了吴文俊，并要求他必须报考上海交大数学系。就此，他进入名校。

与国内其他的大学相比，上海交大数学系成立较晚，课程偏重计算而理论较少。大二时，吴文俊对数学失去了兴趣，甚至想辍学了。大三时，由于武崇林讲授代数与实变函数论，才使他对现代数学，尤其是实变函数论产生了浓厚的兴趣。吴文俊在课后刻苦自学，反复阅读相关著作。可以说，他的现代数学基础主要是靠大三大四自学而成的。

1940年，吴文俊大学毕业后，先后在上海的两所中学工作。幸运的是， 他后来遇到了陈省身先生 。

抗日战争胜利后，吴文俊到上海临时大学任教。次年4月，陈省身从美返国，在上海筹组中央研究院数学研究所。经过他人介绍，吴文俊来到数学所工作。他受到陈省身的严格训练，开始接触到拓扑学，从过去偏狭的古老学科转向新兴学科。

不久， 开始独立研究的吴文俊便对示性类的对偶定理 ，给出了一个简单的证明。这一重要成果现已成为经典。

1947年11月，吴文俊考取了中法交换生赴法留学，两年后拿到博士学位。之后他在法国做出了一些比较重要的成果。

1951年， 具有强烈爱国心的吴文俊放弃了在法国的优越条件而回国 ，先在北大数学系任教，一年后调到新成立的中科院数学所。

此后5年，他刻苦钻研，引进的示性类和示嵌类被称为“吴示性类”和“吴示嵌类”，导出的示性类之间的关系式被称为“吴公式”。

他的工作是1950年代前后拓扑学的重大突破之一 ，成为影响深远的经典性成果。他的工作也曾被5位国际数学最高奖——菲尔兹奖得主引用，其中3位还在他们的获奖工作中使用了吴文俊的结果。

由于吴文俊在拓扑学示性类及示嵌类方面的贡献，1956年他荣获了第一届国家自然科学一等奖，并于1957年增选为中科院学部委员。

然而，随后吴文俊却遭遇了不顺。

从1958年起，吴文俊的拓扑学研究工作被迫中断，他只能做一些“理论联系实际”的工作。

1962年，形势变化，吴文俊又重新开始了拓扑学的研究。但两年后他的拓扑学研究再次停滞。

1972年，科研工作部分恢复。再两年后吴文俊的兴趣转向中国数学史，用算法及可计算性的观点来分析中国古代数学。此后。 吴文俊终于走上了凭着兴趣研究的“顺”时 。

已近花甲之时，吴文俊接触到了计算机。为了验证自己所提出的机器证明方法的有效性，他开始学习计算机编程，用Fortran语言实现了符号计算和几何定理证明的算法。编程的工作量是巨大的， 他每天10多个小时在机房连续工作 。

他从几何定理机器证明与议程求解两个具体研究方向入手 ，创造了新的方法，开创了崭新的数学机械化领域，提出了用计算机证明几何定理的“吴方法”，这被认为是自动推理领域的先驱性工作。正因此，他获得了国际自动推理最高奖“Herbrand自动推理杰出成就奖”。

斯人已去，世间犹存“吴方法”

符号主义和连接主义是人工智能方法两大流派 。在历史上，作为连接主义的代表，人工神经网络几经沉浮，目前攀上发展的巅峰，高歌猛进、如火如荼；而符号主义发展的巅峰之一，正是吴文俊先生开创的机器定理证明。

吴先生曾经指出，源自希腊的西方数学主要遵循“公理化”的原则来搭建理论大厦。

公理化系统首先建立一系列“不可辩驳”的公理（axioms），然后通过逻辑演算来推演引理、定理和推论，从而推演出整个理论体系。只要承认公理，那么所有的推导结果必然自动为真。特别是所有的推演过程都可以严格检验，由机械完成。在数学的所有分支几乎都是以公理化系统为历史总结，成为这一分支成熟的标志，例如同调论（homology Theory）。饶有兴味的是，在数学中许多艰深的概念由于过于抽象，无法直接描述， 反而以更为抽象的公理化方法来加以定义 。

历史上，以希尔伯特（Hilbert）为代表的数学家力图用公理化方法来统一整个数学，建立一个包罗万象的公理系统，来囊括所有的数学真理。哥德尔的不完备性定理否定了这一宏伟蓝图。哥德尔证明任意一个包含初等数论的公理系统，并且是自洽的，它必定包含某些命题，这些命题的真伪无法被该系统证明；如果此系统无矛盾，则其无矛盾性不可能在此系统内证明。这意味着，对于任意包含有限公理的形式系统，存在一条数学真理，此系统可以表述但是无法证明，因此真理的探索过程是无止境的； 同时，这一系统的无矛盾性，必须由其他系统来证明 。这种现象比比皆是，例如某一数学领域最为根本的定理，往往用另外数学领域的方法来证明，代数的基本定理是说多项式方程存在根，这一定理只能用拓扑方法来证明。

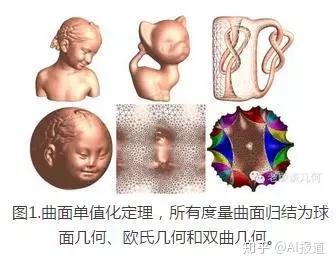
欧几里得几何的公理体系不包含初等数论，它是完备的。长期以来，人类经过大量的生产实践，都认为欧几里得几何的几条公理不证自明，是唯一“真实”的几何。后来，罗巴切夫斯基将第五公设“过直线外一点存在一条平行线”修改成“过直线外一点存在无穷多条平行线”，通过逻辑演绎，建立了双曲几何。如果将此公设改成“过直线外一点不存在平行线”， 则可以得到球面几何 。长期以来，人们一直将双曲几何和球面几何作为纯粹智力游戏的产物，倾向于认为它们没有真实的物理基础。依随科学的发展，欧氏几何、球面几何和双曲几何都成为黎曼几何的特例，广义相对论的建立使人们相信黎曼几何物理真实性，从而不再纠结逻辑演绎结论的物理基础。历史的发展总是依循“否定之否定”的规律，共形几何的发展揭示了所有的二维黎曼流形，在保角变换下都可以归结为球面几何、欧氏几何和双曲几何中的一种，如图1所示。近些年来，依随计算机科学的发展，几乎所有的曲面几何计算问题都可以归结在这些标准空间中的计算问题， 因此对于这三种古老而“正统”的几何研究日益复苏 。

吴文俊先生为了弘扬中国数学构造性算法化的传统，将数学（特别是代数几何）与计算机科学相结合，开创了机器几何定理证明的方向 ，只手擎天地推动了数学机械化的发展。吴先生认为在很大程度上，人们可以用复杂的计算推演来代替抽象的推理，从而用计算机来辅助数学家去发现自然结构、获取数学真理。吴先生发明的吴方法，完全可以证明所有欧几里得几何的定理，同时被广泛应用于许多数学和工程领域。

机器几何定理证明

基于吴方法的自动几何定理定理证明大致步骤如下：

3. 用三角列中的多项式伪除结论多项式，如果余式非0，则我们说命题不成立；

4. 检查非退化条件，如果非退化条件满足（所有初式的乘积非零），则我们说结论多项式由条件多项式生成。

我们可以用吴方法来证明结论多项式可以由条件多项式推出，从而证明了垂心定理。很多时候， 机器给出的证明非常出人意料，更为简洁巧妙 。

机器人路径规划

吴方法可以用来求解多项式方程组。

在机器人应用中，机器人通过三维扫描获得物体的三维几何位置信息，从而得到最终机械手的位置和朝向，通过反解各个关节的旋转角度，和机械臂的伸缩，使得机械手达到目标位置，从而可以实现抓取。这被称为是逆向运动学问题（inverse kinematics），需要求解多项式方程组，而吴方法正是解多项式方程组的有力武器。

吴方法提供了非常基本的算法，能够求解多项式方程组，证明初等几何定理，计算机器人路径规划，生成数控机床加工方案，进行参数样条曲面隐式化，求解代数几何问题等等， 从而广泛应用于纯粹数学、计算数学以及众多工程领域 。

吴方法为人工智能的符号计算提供了坚实的理论基础和高效的算法，特别是算法的每一步骤都可以被人类透彻理解，它代表了智能中严密清晰的逻辑思维层面，和连接主义中概率模糊的感性直觉层面互补。

我们相信，在未来，吴方法必将在人工智能领域再放异彩。吴文俊先生的光辉思想将会被后人深入挖掘，继承发扬，彪炳千秋！