相关文章推荐
小百科  ›  PSM与DID的结合是一段“孽缘” -
孽缘
冷冷的单杠
9 月前
首发于 功夫计量经济学
PSM与DID的结合是一段“孽缘”

PSM与DID的结合是一段“孽缘”

许久以来，很多朋友都希望我出一期有关双重差分倾向得分匹配方法（PSM-DID）的内容，但我一直迟迟没有动笔。事实上，我个人并不喜欢这一方法，也并不推荐大家使用这一方法，因为 PSM-DID压根就不是什么“灵丹妙药”，在应用中问题颇多 。也许你在一些top期刊上经常看到PSM-DID的身影，但这并不意味着它就没有问题。

双重差分倾向得分匹配方法（PSM-DID）是倾向得分匹配（PSM）与双重差分法（DID）的有机结合（DID是主，PSM是次），但是这一结合事实上就是一段“孽缘”。我们的理想很美好，PSM模型负责寻找与处理组尽可能相似的控制组（根据倾向得分），DID模型负责评估政策带来的影响。

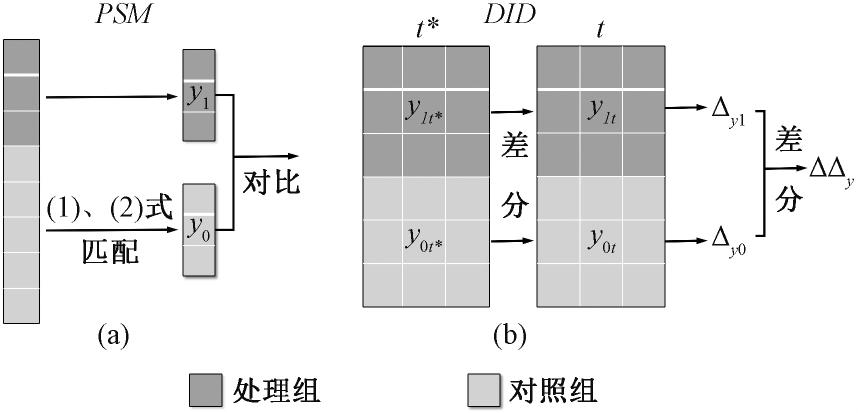
图片来源：谢申祥、范鹏飞和宛圆渊（2021）论文《传统PSM-DID 模型的改进与应用》

然而现实很残酷， PSM模型适用于截面数据，而DID适用于面板数据 。二者适用的数据类型不同，如何在面板数据中应用PSM模型就成了PSM-DID模型无法回避的问题，为了解决这一问题，学者们一般有两种解决方案， 一种是将面板数据当做横截面数据进行处理（混合匹配），另一种是在面板数据的每期截面上进行逐期匹配 。事实上，这两种方案都并不完善，下面我将分别阐述它们在应用中所存在的问题。

混合匹配

混合匹配是将面板数据当做横截面数据进行处理，为处理组的每条观测值匹配一条控制组的观测值。接下来，我就使用石大千等（2018）发表在《中国工业经济》上的论文《智慧城市建设能否降低环境污染》使用的数据，给大家展示一下混合匹配的Stata操作以及混合匹配带来的问题。

原文信息
石大千,丁海,卫平,刘建江.智慧城市建设能否降低环境污染[J].中国工业经济,2018(06):117-135.

首先，我们需要产生随机数，对样本进行排序。为了保证结果可复现，我就设定种子值为 20210415 。 

set seed 20210415
gen tmp=runiform()
sort tmp

接下来，我们可以使用 psmatch2 命令（外部命令需要安装 ssc install psmatch2, replace ）进行倾向得分匹配，我选择的匹配方法是一对一近邻匹配。其中， du 是处理组虚拟变量； $xlist 是协变量（控制变量）；选择项 out() 用来指定结果变量 y ，这里填入DID模型的被解释变量即可；选择项 logit 表示使用logit模型来估计倾向得分，默认方法是probit；选择项 common 表示仅对共同取值范围内个体进行匹配；选择项ate表示同时汇报ATE、ATU和ATT。 

. psmatch2 du $xlist , out(lnrso) logit neighbor(1) common ate //近邻匹配

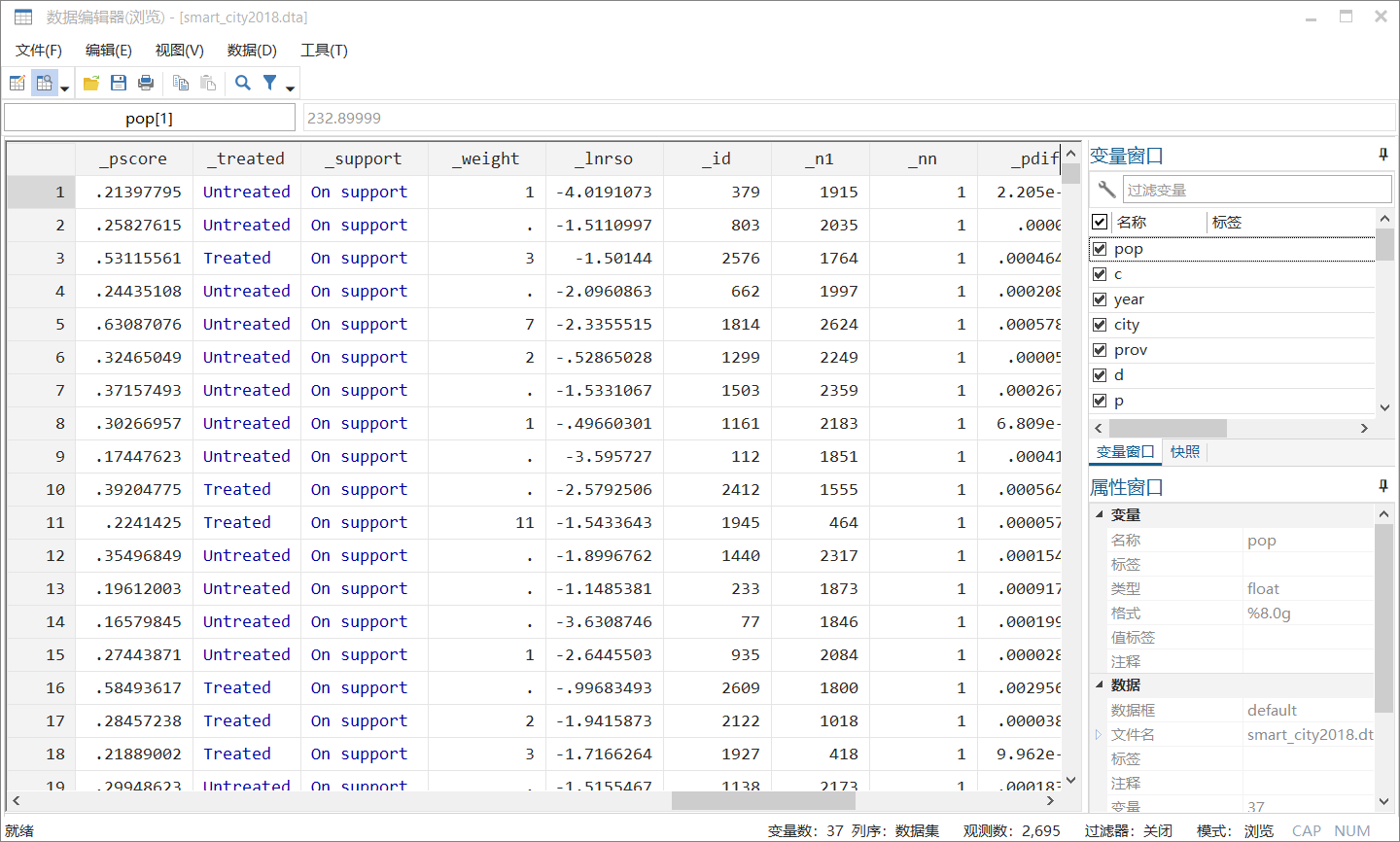
打开数据编辑窗口，我们会发现软件自动生成了几个新变量。其中 _pscore 是每个观测值对应的倾向得分； _treated 表示某个对象是否处理组； _support 表示观测对象是否在共同取值范围内； _weight 是观测对象用于匹配的频率，如果 _weight 为空值，那就说明虽然你看上了对方（会有一个匹配对象），但是你并没有被对方看上（对方匹配上的不是你）； _id 是自动生成的每一个观测对象唯一的ID； _n1 表示的是他被匹配到的对照对象的 _id （如果是1:3匹配，还会生成_n2, _n3）； _pdif 表示一组匹配了的观察对象他们概率值的差。

最后，我们只需去掉匹配不成功的样本（即 _weight 为空值的样本），然后再用DID方法去进行估计就可以了。PSM-DID估计结果显示，交互项 dudt 的系数为-0.1781016，表明智慧城市建设显著降低了约17.81%的人均废气排放量。 

. drop if _weight==.
(1,467 observations deleted)
. reghdfe lnrso dudt $xlist ,absorb(c year) vce(cluster c) //DID估计
(dropped 21 singleton observations)
(MWFE estimator converged in 7 iterations)
HDFE Linear regression                            Number of obs   =      1,207
Absorbing 2 HDFE groups                           F(   7,    218) =       2.12
Statistics robust to heteroskedasticity           Prob > F        =     0.0423
                                                  R-squared       =     0.8880
                                                  Adj R-squared   =     0.8608
                                                  Within R-sq.    =     0.0350
Number of clusters (c)       =        219         Root MSE        =     0.4147
                                    (Std. Err. adjusted for 219 clusters in c)
------------------------------------------------------------------------------
             |               Robust
       lnrso |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        dudt |  -.1781016   .0834432    -2.13   0.034    -.3425604   -.0136429
      lnrgdp |   2.101315   1.207922     1.74   0.083    -.2793847    4.482014
      lntgdp |  -.0910883   .0572348    -1.59   0.113    -.2038928    .0217162
      lninno |   .1235118   .0676161     1.83   0.069     -.009753    .2567767
       lnurb |   .1283764    .064476     1.99   0.048     .0013002    .2554525
      lnopen |   .0317352   .0459506     0.69   0.491    -.0588291    .1222995
        lnss |  -.1781226   .3485232    -0.51   0.610     -.865029    .5087837
       _cons |  -13.93434   6.665826    -2.09   0.038    -27.07205   -.7966249
------------------------------------------------------------------------------
Absorbed degrees of freedom:
-----------------------------------------------------+
 Absorbed FE | Categories  - Redundant  = Num. Coefs |
-------------+---------------------------------------|
           c |       219         219           0    *|
        year |        11           0          11     |
-----------------------------------------------------+
* = FE nested within cluster; treated as redundant for DoF computation

不过，这一估计结果并不可信，因为混合匹配存在“时间错配”的问题，即某一期的处理组观测对象，可能与不同期的控制组观测对象相匹配。例如，你会惊奇的发现，2006年的遵义市居然匹配上的是2014年的佳木斯市，时隔八年，还有什么可比性呢？这种“时间错配”现象在混合匹配中是一种常态，它带来的后果就是我们无法有效控制时间固定效应，从而使得DID估计产生偏差。 

. list c year city prov _treated _id _n1 if _id==379|_id==1915
      +------------------------------------------------------------+
      |   c   year       city       prov    _treated    _id    _n1 |
      |------------------------------------------------------------|
   1. |  61   2014   佳木斯市   黑龙江省   Untreated    379   1915 |
1220. | 242   2006     遵义市     贵州省     Treated   1915    379 |
      +------------------------------------------------------------+

很多中文论文在使用PSM-DID方法时，对于匹配的细节都“缄口不言”，加之又没有要求公布数据和代码，所以我们并不知道哪些中文文献使用了这种“糟糕的”匹配方案，但我估计应该不在少数。我们不能说混合方案就是错的，毕竟也算是一种匹配的“野路子”，但我还是建议大家不要使用混合匹配！

逐期匹配

逐期匹配是在面板数据的每期截面上都进行一次匹配。逐期匹配能够较好地解决“时间错配”问题，但这种匹配方案也存在缺陷——对照组的不稳定性（逐期匹配不能为DID模型筛选到稳定的对照组，处理组个体 i 在每期的匹配对象可能均不相同，混合匹配当然也存在这一问题）。对于同一个处理组个体，其对照对象如果在政策时点前后发生较大改变，将会导致个体固定效应的估计出现偏差，进而影响到DID模型的稳定性。除此之外，逐期匹配存在着其他问题，大家有兴趣可以去阅读《传统PSM-DID模型的改进与应用》这篇论文。

参考资料（推荐阅读）
谢申祥,范鹏飞,宛圆渊.传统PSM-DID模型的改进与应用[J].统计研究,2021,38(02):146-160.

相比混合匹配，逐期匹配算是一种差强人意的解决方案，也是top期刊论文使用较多的匹配方案。逐期匹配的Stata操作其实也很简单，首先分年份进行匹配，然后保存每一年的匹配结果，最后合并各个年份的匹配结果就好（借用循环很方便）！ 

forvalues i = 2005/2015{
 use smart_city2018.dta,clear
 keep if year==`i'
 set seed 20210415
 gen tmp=runiform()
 sort tmp
 psmatch2 du $xlist , out(lnrso) logit neighbor(1) common ate
 drop if _weight==.
 save psmdid_`i',replace
 
推荐文章
Link管理   ·   51好读   ·   Sov5搜索   ·   小百科
小百科 - 百科知识指南