金融工程笔记3:Black-Scholes-Merton期权定价模型
- Black-Scholes-Merton方程
之前已经建立了股票价格的几何布朗运动模型,现在在此基础上推导出无股息股票衍生品所满足的方程,也就是Black-Scholes-Merton方程。基本思路就是构造一个期权与标的股票所组成的无风险交易组合(收益无不确定性),在无套利原则下,该组合收益等于无风险利率带来的收益,利用该等式可以进一步得出期权价格所满足的方程。
1.1 Black-Scholes-Merton方程推导
假设:
a)无交易成本。
b)股票无股息。
c)股票价格服从几何布朗运动,即股票在时间 t 的价格为 S_{t} , S_{t} 是一个随机过程,满足随机微分方程 dS_{t} = \mu S_{t}dt+\sigma S_{t} dW_{t},W_{t}\sim N(0,t) ,其中 \mu 是股票期望年对数收益率, \sigma 是股票年对数收益率的方差(波动率)。 t 的单位是年,一般是期限内有效交易天数/一年内有效交易天数。
设无风险收益率为 r ,标的为满足以上假设的股票的期权在时间 t 的价格为 c_{t} ,则 c_{t} 为 t 和 S_{t} 的函数,记为 c_{t}=f(t,S_{t}) 。
根据伊藤引理,可得到 c_{t} 满足随机微分方程
dc_{t} = (\frac{\partial f}{\partial t}+\mu S_{t} \frac{\partial f}{\partial S_{t}}+\frac{\sigma^2}{2}S^2_{t}\frac{\partial ^2f}{\partial S^2_{t}})dt +\sigma S_{t}dW_{t}
现在把股票价格 S_{t} ,和相应期权价格 c_{t} 所满足的随机微分方程写为增量形式得
S_{t+\Delta t}-S_{t}=\mu S_{t}\Delta t+\sigma S_{t}(W_{t+\Delta t}-W_{t}) (1.1)
c_{t+\Delta t}-c_{t}=(\frac{\partial f}{\partial t}+\mu S_{t} \frac{\partial f}{\partial S_{t}}+\frac{\sigma^2}{2}S^2_{t}\frac{\partial ^2f}{\partial S^2_{t}})\Delta t +\sigma S_{t}\frac{\partial f}{\partial S_{t}} (W_{t+\Delta t}-W_{t}) (1.2)
现在构建期权与标的股票得无风险收益组合 \pi ,设在这个组合中有1个期权空头并有 x 个股票多头,则组合价格可以表示为
\pi _{t} = xS_{t}-c_{t}=xS_{t}-f (1.3)
组合价格增量可以表示为
\pi _{t+\Delta t}-\pi_{t}=x(S_{t+\Delta t}-S_{t})-(c_{t+\Delta t}+c_{t}) (1.4)
现在把(1.1)、(1.2)带入(1.4)可进一步把组合价值增量表示为
\pi _{t+\Delta t}-\pi_{t}=[(x-\frac{\partial f}{\partial S_{t}})\mu S_{t} - \frac{\partial f}{\partial t}-\frac{\sigma^2}{2}S^2_{t}\frac{\partial^2f}{\partial S^2_{t}}]\Delta t
+(x-\frac{\partial f}{\partial S_{t}})\sigma S_{t} (W_{t+\Delta t}-W_{t}) (1.5)
组合价格增量 \pi _{t+\Delta t}-\pi_{t} 可以视为该组合在时间 [t,t+\Delta t] 产生的收益,观察(1.5),组合收益有一随机项 W_{t+\Delta t}-W_{t} ,若消去这一项,则组合在在时间 [t,t+\Delta t] 产生的收益就是无风险的,不难发现令期权与标的股票的投资组合中一个期权空头所对应的股票多头个数 x = \frac{\partial f}{\partial S_{t}} 就可以消去随机项。
现在可以得到期权与标的股票所组成的无风险交易组合为持有一个期权空头的同时持有 \frac{\partial f}{\partial S_{t}} 个股票多头,根据(1.3)、(1.5)组合在 t 价格和组合在时间 [t,t+\Delta t] 产生的收益分别为
\pi _{t} =\frac{\partial f}{\partial S_{t}}S_{t}-f (1.6)
\pi _{t+\Delta t}-\pi_{t}=( - \frac{\partial f}{\partial t}-\frac{\sigma^2}{2}S^2_{t}\frac{\partial^2f}{\partial S^2_{t}})\Delta t (1.7)
此时组合在时间 [t,t+\Delta t] 产生的收益(1.7)是无风险的,它的收益必等于无风险利率在时间 [t,t+\Delta t] 产生的收益,所以可以得到等式
( - \frac{\partial f}{\partial t}-\frac{\sigma^2}{2}S^2_{t}\frac{\partial^2f}{\partial S^2_{t}})\Delta t = \pi_{t}r\Delta t (1.8)
把(1.5)带入(1.8)右边整理得 f 所满足的偏微分方程,即 Black-Scholes-Merton方程:
\frac{\partial f}{\partial t}+rS_{t}\frac{\partial f}{\partial S_{t}} +\frac{\sigma^2}{2}S^2_{t}\frac{\partial^2f}{\partial S^2_{t}} = rf (1.9)
1.2 Black-Scholes-Merton方程应用
(1)根据边值条件构建无股息股票衍生品无套利价格
在无套利条件下无股息股票衍生品必满足方程(1.9),在已知该衍生品价格的边值条件下,利用(1.9)可以构造其价格。
例如要求某衍生品当股票价格第一次到达价格 H 时,有固定收益 Q ,衍生品对于任意的股票价格 S ,其价值与时间 t 无关。当 S=0 时, f=0 ;当 S=H 时, f=Q ;当 S\rightarrow + \infty , f = 0 。
此时可以设 f = Q(\frac{S}{H})^{-\alpha},\alpha >0 ,则 f 满足以上边值条件,利用方程(1.9),可以解出 \alpha ,从而确定衍生品价格 f 。
将计算结果
\frac{\partial f}{\partial t}=0
\frac{\partial f}{\partial S}=-\alpha \frac{Q}{H}(\frac{S}{H})^{-\alpha-1}
\frac{\partial ^2f}{\partial S^2}=\alpha(\alpha +1)\frac{Q}{H^2}(\frac{S}{H})^{-\alpha-2}
带入方程(1.9)得
(\frac{\sigma^2}{2}\alpha-r)(\alpha+1)=0
从而可以得出 \alpha = \frac{2r}{\sigma^2}
最终可以得到 f = Q(\frac{S}{H})^{-\frac{2r}{\sigma^2}}
(2)判断某无股息股票衍生品定价是否存在套利机会以及某个 f 是否是衍生品价格
若某衍生品价格 f(S,t) 满足方程(1.9)则不存在任何套利机会,否则可以套利。注意,若谋个 f(S,t) 不满足方程(1.9),且没有任何套利机会,则 f(S,t) 必定不是无股息股票衍生品价格。
例如 e^S 不满足(1.9),则它肯定不是无股息股票衍生品得价格。若市场上某无股息股票衍生品价格为 e^S ,则它一定存在套利机会。
再例如 \frac{e^{(\sigma^2-2r)(T-t)}}{S} 满足(1.9),所以从理论上讲,这一函数是某个无股息股票衍生品的价格。
2. Black-Scholes-Merton期权定价公式
Black-Scholes-Merton无股息股票期权定价公式可以利用风险中性定价的方法得到。
2.1 风险中性定价
风险中性定价
指,在对期权进行定价时假设投资者是风险中性的。具体指投资风险增长时投资人并不需要额外的预期回报率。
风险中性世界
指所有的投资人都是风险中性的。
在风险中性世界中,有两个重要特点:
(1)所有投资期望收益率等于无风险利率,对与股票 \mu =r 。
(2)对期权(或其他证券)期望收益的贴现使用无风险利率。
注意:在风险中性定价下得到的无股息股票期权定价结果不仅仅在风险中性世界成立,在所有世界都成立,比如把风险中性世界变换到风险厌恶世界,股票价格变动的增长率期望以及对其衍生品收益所必须的贴现率都会发生变化,而这种变化可以相互抵消。
2.2 Black-Scholes-Merton期权定价公式推导
设期权期限为 T ,交割价格为 K ,若不做具体说明,则文中期权指欧式期权。
无股息股票看涨期权(call option)到期收益为 max(S_{T}-K,0)=(S_{T}-K)^+
无股息股票看跌期权(put option)到期收益为
max(K-S_{T},0)=(K-S_{T})^+
假设:
(1)无股息股票价格服从几何布朗运动。
(2)风险中性世界。
即无股息股票期权价格等于其期望收益再用无风险利率进行贴现。则看涨期权、看跌期权价格分别为:
c = e^{-rT}E(S_{T}-K)^+
p = e^{-rT}E(K-S_{T})^+
此外对于股票,对数期望收益率 \mu =r 。
根据假设(1)、(2) lnS_{T}\sim N(lnS_{0}+(r-\frac{\sigma^2}{2})T,\sigma^2T)
令 x\sim N(0,1) ,且 N(x) 为 x 分布函数,则有
S_{T}=S_{0}exp((r-\frac{\sigma^2}{2})T+\sigma \sqrt T x)
c = e^{-rT}E(S_{T}-K,0)^+
=e^{-rT}\int_{-\infty}^{\infty}(S_{0}exp((r-\frac{\sigma^2}{2})T+\sigma \sqrt T x)-K)^+\frac{1}{\sqrt {2\pi}}exp(-\frac{x^2}{2})dx
因为 S_{0}exp((r-\frac{\sigma^2}{2})T+\sigma \sqrt T x)-K\geq 0
\Leftrightarrow x\geq \frac{1}{\sigma \sqrt T}(ln\frac{K}{S_{0}}-(r-\frac{\sigma^2}{2})T)=x^*
所以
c = e^{-rT}\int_{x^*}^{\infty}(S_{0}exp((r-\frac{\sigma^2}{2})T+\sigma \sqrt T x)-K)\frac{1}{\sqrt {2\pi}}exp(-\frac{x^2}{2})dx
=S_{0}\int_{x^*}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(x-\sigma\sqrt T)^2}dx-Ke^{-rT}(1-N(x^*))
=S_{0}[1-N(x^*-\sigma \sqrt T)]-Ke^{-rT}(1-N(x^*))
=S_{0}N(\sigma \sqrt T-x^*)-Ke^{-rT}N(-x^*)
记
d_{1}=\sigma \sqrt T-x^*=\sigma \sqrt T-\frac{1}{\sigma \sqrt T}(ln\frac{K}{S_{0}}-(r-\frac{\sigma^2}{2})T)
=\frac{ln\frac{S_{0}}{K}+(r+\frac{\sigma^2}{2})T}{\sigma \sqrt T}
d_{2}=-x^*=\frac{ln\frac{S_{0}}{K}+(r-\frac{\sigma^2}{2})T}{\sigma \sqrt T}
则
c=S_{0}N(d_{1})-Ke^{-rT}N(d_{2})
同理可得
p = -S_{0}N(-d_{1})+Ke^{-rT}N(-d_{2})
在满足以上条件下现在可以得到 Black-Scholes-Merton期权定价公式:
c=S_{0}N(d_{1})-Ke^{-rT}N(d_{2})
p = -S_{0}N(-d_{1})+Ke^{-rT}N(-d_{2})
其中
d_{1}=\frac{ln\frac{S_{0}}{K}+(r+\frac{\sigma^2}{2})T}{\sigma \sqrt T}
d_{2}=\frac{ln\frac{S_{0}}{K}+(r-\frac{\sigma^2}{2})T}{\sigma \sqrt T}=d_{1}-\sigma\sqrt T
2.3 Black-Scholes-Merton期权定价公式说明
a)不支付股息的股票美式期权永远不会是最优的,所以Black-Scholes-Merton期权定价公式值并不是美式期权的价值。
b)当 r 为时间 t 的有效函数时,Black-Scholes-Merton期权定价公式依然成立;当 lnS_{t} 服从正态分布,且波动率选取得当,若 r 为随机变量,Black-Scholes-Merton期权定价公式也成立。
c)一些参数意义
(1) 看涨期权被行使的概率
P(S_{T}-K\geq 0)=P(lnS_{T}\geq lnK)=1-N(\frac{lnK-lnS_{0}-(r-\frac{\sigma^2}{2})T}{\sigma\sqrt T})
=N(\frac{ln\frac{S_{0}}{K}+(r-\frac{\sigma^2}{2})T}{\sigma \sqrt T})=N(d_{2})
(2)看跌期权被行使的概率
P(K-S_{T}\geq 0)=P(lnS_{T}\leq lnK)=N(\frac{lnK-lnS_{0}-(r-\frac{\sigma^2}{2})T}{\sigma \sqrt T})
=1-N(d_{2})=N(-d_{2})
(3)期权定价公式的等价形式
c=e^{-rT}[N(d_{2})(S_{0}\frac{e^{rT}N(d_{1})}{N(d_{2})}-K)+(1-N(d_{2}))0]
则若看涨期权被行使,则股票价格预期增长率为 \frac{e^{rT}N(d_{1})}{N(d_{2})} ,股票价格在 T 为 S_{0}\frac{e^{rT}N(d_{1})}{N(d_{2})} 。
p=e^{-rT}[N(-d_{2})(K-S_{0}\frac{e^{rT}N(-d_{1})}{N(-d_{2})})+(1-N(-d_{2}))0]
则若看跌期权被行使,则股票价格预期增长率为 \frac{e^{rT}N(-d_{1})}{N(-d_{2})} ,股票价格在 T 为 S_{0}\frac{e^{rT}N(-d_{1})}{N(-d_{2})} 。
d)隐含波动率
B-S定价公式中,不能直接观察到的只有波动率 \sigma 。 隐含波动率 是指在给定 S_{0} 、 T 、 K 、 r 与相应的 c 或 p 的条件下B-S定价公式所隐含的 \sigma 。
首先注意的是 c 和 p 是关于 \sigma 的增函数,因为看涨期权可以从标的股票价格上涨获利,而股票价格下跌损失至多只是期权费用;看跌期权可以从标的股票价格下跌获利,而股票价格上涨损失也至多是期权费用。
在除波动率以外其他参数以知的情况下,求解B-S公式所隐含的 \sigma 本质上是一个方程求根问题,最简单可利用二分法来求。
3. 有股息情形的期权定价
设股票在期限 [0,T] 有n个除息日 0\leq t_{1}<t_{2} <...<t_{n}\leq T ,除息日股息为 D_{i} ,则利用无风险利率 r 对股息总额进行贴现有 D = \sum_{i=1}^{n}{D_{i}e^{-rt_{i}}} 。(注意时间单位为年)
在B-S公式中将 S_{0} 调整为 S^*_{0} ,其中 S^*_{0}=S_{0}-D 。
4. python期权价格计算
4.1 B-S公式期权定价
a)一个期权价格计算
定义函数
from math import log, sqrt, exp
from scipy.stats import norm
spot = 2.45
strike = 2.50
maturity = 0.25
r = 0.05
vol = 0.25
def call_option_pricer(spot, strike, maturity, r, vol):
d1 = (log(spot/strike) + (r + 0.5 * vol *vol) * maturity) / (vol * sqrt(maturity))
d2 = d1 - vol * sqrt(maturity)
price = spot * norm.cdf(d1) - strike * exp(-r*maturity) * norm.cdf(d2)
return price
def put_option_pricer(spot, strike, maturity, r, vol):
d1 = (log(spot/strike) + (r + 0.5 * vol *vol) * maturity) / (vol * sqrt(maturity))
d2 = d1 - vol * sqrt(maturity)
price = -spot * norm.cdf(-d1) + strike * exp(-r*maturity) * norm.cdf(-d2)
return price打印输出
print("看涨期权价格{0}元,看跌期权价格{1}元".format(call_option_pricer(spot, strike, maturity, r, vol),put_option_pricer(spot, strike, maturity, r, vol)))输出结果
看涨期权价格0.11332871320482885元,看跌期权价格0.13227321443953222元
b)批量期权价格计算
numpy内置数学函数可以用于计算向量参数,可以让我们在批量计算期权价格时减少for循环。
# 基于Black - Scholes 公式的期权定价公式
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
spot = 2.45
strike = 2.50
maturity = np.linspace(0,1,1000)
r = 0.05
vol = 0.25
# 使用numpy的向量函数重写Black - Scholes公式
def call_option_pricer_nunmpy(spot, strike, maturity, r, vol):
d1 = (np.log(spot/strike) + (r + 0.5 * vol *vol) * maturity) / (vol * np.sqrt(maturity))
d2 = d1 - vol * np.sqrt(maturity)
price = spot * norm.cdf(d1) - strike * np.exp(-r*maturity) * norm.cdf(d2)
return price
def put_option_pricer_nunmpy(spot, strike, maturity, r, vol):
d1 = (np.log(spot/strike) + (r + 0.5 * vol *vol) * maturity) / (vol * np.sqrt(maturity))
d2 = d1 - vol * np.sqrt(maturity)
price = -spot * norm.cdf(-d1) + strike * np.exp(-r*maturity) * norm.cdf(-d2)
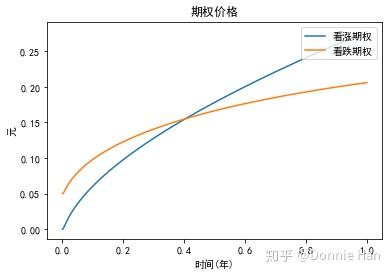
return price批量期权计算结果图示
a = call_option_pricer_nunmpy(spot, strike, maturity, r, vol)
b = put_option_pricer_nunmpy(spot, strike, maturity, r, vol)
option = np.vstack((a,b))
lab = np.array(['看涨期权','看跌期权'])
for i in np.arange(option.shape[0]):
plt.plot(maturity,option[i,:],label= lab[i])
plt.legend(loc='upper right')
plt.xlabel('时间(年)')
plt.ylabel('元')
plt.title('期权价格')
plt.show()输出结果
4.3 蒙特卡洛法计算期权价格
a)标的为无股息股票的欧式期权价格计算
(1)抽取标准正态分布随机数 \left\{ \varepsilon_{i} \right\}_{i=1}^{N}\sim N(0,1)
(2)得到期限 T 到期股票价格样本 \left\{ S^{(i)}_{T} \right\}_{i=1}^{N} ,其中 S^{(i)}_{T}=S_{0}exp((r-\frac{\sigma^2}{2})T+\sigma \sqrt T\varepsilon_{i})
(3) c\approx e^{-rT}\frac{1}{N}\sum_{i=1}^{N}{(S^{(i)}_{T}-K)^+}
p\simeq e^{-rT}\frac{1}{N}\sum_{i=1}^{N}{(K-S^{(i)}_{T})^+}
python蒙特卡洛法计算期权价格:
import numpy as np
import scipy as sy
spot = 2.45
strike = 2.50
maturity = 0.25
r = 0.05
vol = 0.25
# 期权计算的蒙特卡洛方法
def call_option_pricer_monte_carlo(spot, strike, maturity, r, vol, N = 5000):
randomSeries = sy.random.randn(N) #N个正态分布随机数
s_t = spot * np.e**((r - 0.5 * vol * vol) * maturity + randomSeries * vol * np.sqrt(maturity))
sumValue = np.maximum(s_t - strike, 0.0).sum()
price = np.e**(-r*maturity) * sumValue / N
return price
def put_option_pricer_monte_carlo(spot, strike, maturity, r, vol, N = 5000):
randomSeries = sy.random.randn(N)
