对本征方程求解可以得到一系列分立的本征值，但也有连续的本征值存在，例如动量的本征值可以取任意实数值。

这种 连续谱 不能像分立谱那样，用本征右矢张成右矢空间然后开始推导其他的东西，因为这样一个空间的维数显然是无穷大的，但我们可以从有限维的分立谱的情况对一些结果进行推广。给出一个连续谱的类似本征方程的方程：

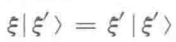
我们用狄拉克δ函数代替克罗内克尔符号，并且用积分代替求和，就会得到下列结果：

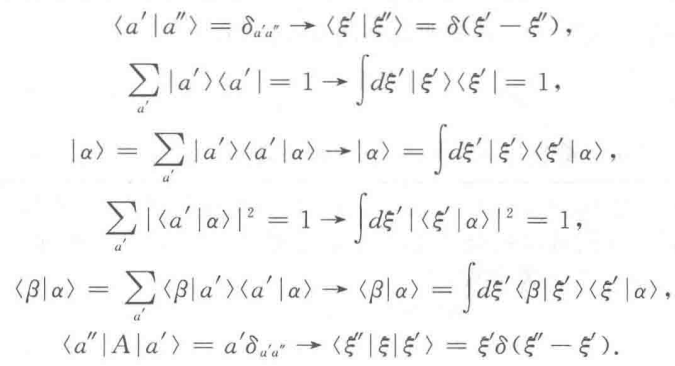
量子力学的测量实际上是一种过滤，现在考虑一个具体的例子：

对一维的 位置 坐标有：

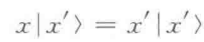
假定上式完备，任意一个物理态的右矢在{|x'>}上展开为：

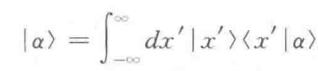
我们需要一个理想的选择性测量实验，假设有一个探测器，当粒子出现在x'处时，探测器作出一次计数，实际上，由于精度限制，探测器最多在x'附近一个小区间进行探测：

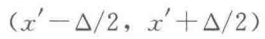
在这个范围内的位置变化，探测器无法区分。

当探测器计数一次，态右矢变成：

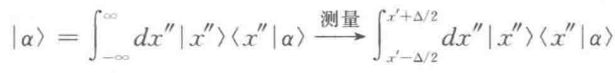
探测器发生计数的概率为：

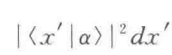
概率是归一化的，当|α>也归一化，就得到

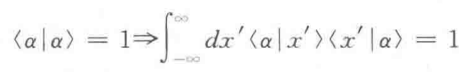
在波动力学里，<x'|α>就是|α>态的波函数，这种展开系数就是波函数的x表象。

接下来把位置坐标拓展到三维，态右矢展开为：

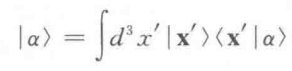
| x' >是三个坐标x，y，z的共同本征右矢：

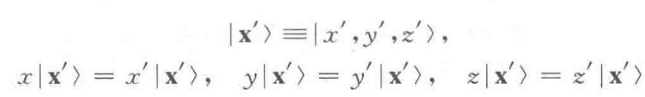
它们满足对易关系：

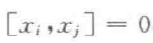
现在引入平移，也就是空间位移的概念。平移的操作通过一个算符进行：

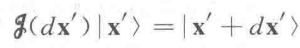
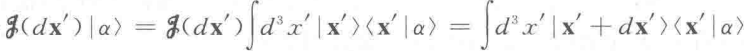
由于积分是在全空间，所以：

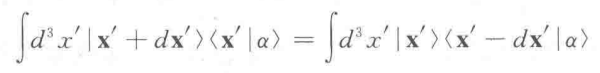
为了保证归一化，我们要求这个平移算符是幺正的：

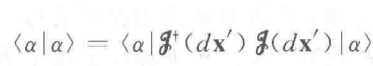
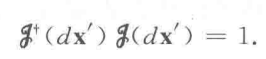
此外，我们期望多次平移可以用一个算符表示：

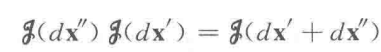
对于反方向平移，则取算符的逆：

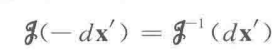
现在假设一种平移算符的形式：

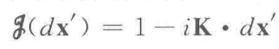
容易证明这个形式满足前面对平移算符的要求，通过这个形式，可以给出算符 K 和算符 x 的关系，首先是：

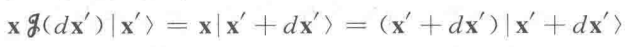
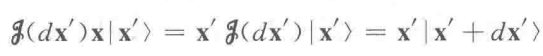
由上两式代入对易关系，给出：

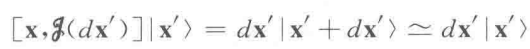
即

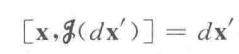
代入算符的形式：

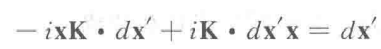
取标量积化成：

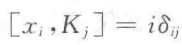
δ包括一个单位算符。

这个 K 算符是什么？我们不妨猜测它和动量有关系，但从量纲来看， K 的量纲必须是1/m，显然和动量不同，但可以这样处理：

观察一下 德布罗意 关系：

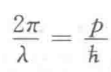
不难发现， K 实际上就是波数k的算符，此时，平移算符又可以写成：

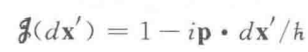
相应的，对易关系变成：

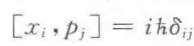
上式说明动量和位置不对易，很久之前我们就讨论过，可以推出 不确定性关系 ：

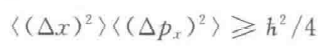
前面一直在讨论无穷小位移，接下来考虑有限的一段位移

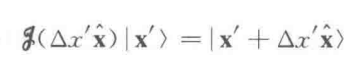
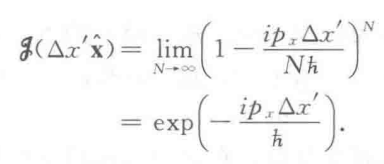
对算符有下列展开：

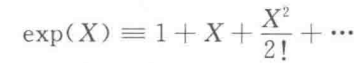
两个不同方向的平移和动量都是对易的

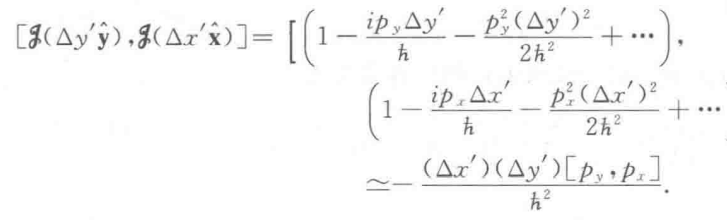
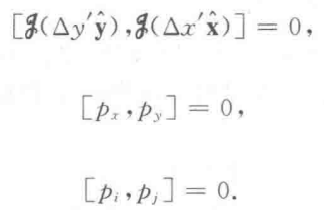
任何情况下，平移的生成元都互相对易，这种群我们称之为 阿贝尔群 ，三维的平移群就是阿贝尔群。既然对易，对动量就有共同本征右矢：

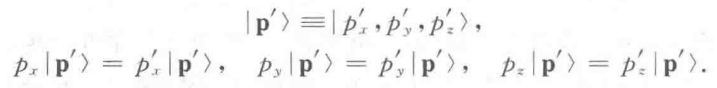
作平移操作：

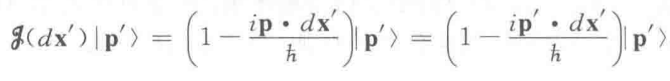
显然，|p'>是平移算符的一个本征右矢。

1925年，狄拉克发现，经典的 泊松括号 可以用对易关系作替换：

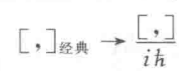
经典泊松括号定义为：

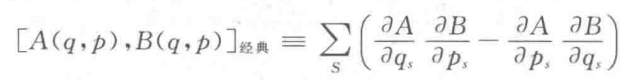
举例来说，经典力学有：

对应量子力学就变成了：

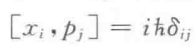
不管怎么称呼，这个括号都有如下性质：

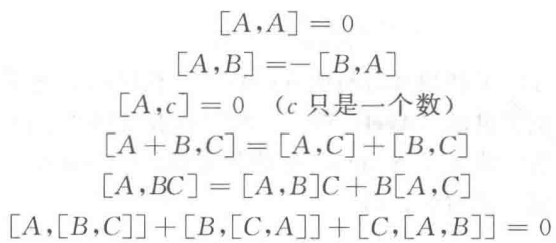
最后一个式子被称为 雅可比恒等式 。