PSM的原理以及stata操作
PSM是解决内生性问题的一大利器,其可以解决的是样本选择带来的内生性问题。
一、PSM方法的简要介绍
例如我们想要研究接受培训对一个人收入的影响,则需要在样本内进行随机分配,一部分接受培训,一部分不接受培训。之后我们将两组的观察结果进行对比,从而可以得出培训对个人收入的净影响。这是因为由于我们的处理变量D1(是否接受培训)是随机的,因此将不会与干扰项相关,不存在内生性问题。
公式如下:
Y=α+β0*D1+β1*Controls+ε \\

但是在实际处理过程当中,D1并不一定是随机分配的,D1很可能会受到样本本身特征的影响,比如说教育程度较高的人更倾向于接受培训,年纪较小的人更倾向于接受培训。因此我们观察到的因变量的变化结果是来自于两个方面的影响:培训和两组之间本身的特征差异。
因此我们在B组当中寻找与A组相似的个体进行匹配,这样的情况下我们就可以剔除特征因素对因变量的影响,使得D1尽可能随机。
二、检验PSM的前提
- 条件独立假设
倾向评分匹配估计的前提是处理组企业和对照组企业是否满足“条件独立性”假设:即当控制了公司层面的特征变量后,员工是否接受培训是否与其工资水平相互独立。
根据倾向性匹配得分将样本分成若干区间,保证每个区间里处理组和控制组的平均倾向性得分相同。
2. 共同支撑条件
匹配前后进行核密度图的对比,若匹配结果较为理想,则匹配之后的两条线很相近。
三、选择PSM的匹配方法:
PSM通过统计学模型对每个观测对每个协变量的综合倾向性得分,再按照倾向性得分是否接近进行匹配。
以分组变量为因变量,用其他可能会影响到结果的变量作为协变量进行Logistic回归。计算每个观测的倾向性指数,指数范围为0-1之间,反映个体被分到实验组的概率。
①1对1匹配:在控制组当中选择与处理组中最近似的样本进行匹配。
优点是匹配样本之间更为近似,偏差比较小;但是缺点是样本匹配量较少,估计的方差较大。
②1对多匹配:在控制组中选择多个样本与处理组进行匹配。
-
优点是匹配的样本比较多,但是控制组中找到的第二和第三个样本的样本近似性会减弱,因此估计的偏差会加大。
-
在选择的时候,可以根据控制组的个数来进行选择。若控制组的样本数量较多时,可以考虑进行1对多匹配,反之可以考虑选择一对一匹配。
1. 最邻近匹配
最近邻匹配代码
近邻匹配法是对处置组中的样本,选择控制组中倾向得分最接近的作为匹配样本。
psmatch2 D1 x1 x2 X3, outcome(y1) logit
neighbor(k)noreplacement
noreplacement:无放回匹配,只限于1:1匹配
psmatch2 D1 X1 X2 x3,outcome(y1) logit
neighbor(k) noreplacement caliper(0.05)2. 半径匹配
半径匹配代码
psmatch2 D1 x1 x2 x3,outcome(y1)radius caliper(0.05)3. 核匹配
核匹配代码
psmatch2 D1 x1 x2 x3,outcome(y1)kernel kerneltype(type) bwidth (real)
*默认使用二次核,默认带宽为0.064. 卡尺匹配
为了解决近邻法可能匹配到倾向性得分差异较大的近邻,卡尺匹配法要求近邻匹配得分差异在一定容忍度(“卡尺”)内。
卡尺匹配法的缺点是,对于如何界定容忍度没有标准的方法。如果容忍度太小,可能匹配的数量较少或没有,方差就较大;如果容忍度较大,可能包括差异大的匹配样本,偏差就较大。
5. 分块匹配法
先将样本按倾向得分划分成N个区间,使得每个区间内处理组和控制组的平均倾向得分和可观测特征都达到均衡,然后通过每个区间内处理组与控制组观测结果的差异得到每个区间的处置效应。
分块匹配法的缺陷是需要确定区间(块)的数量。实际操作当中,很难保证每个变量在每块中都均衡,有时候需要接受个别不重要变量的不均衡。

四、协变量的选取
在进行PSM分析之前,如何选取协变量,则是我们事先需要考虑的一点。我们通过使用 psestimate 命令,通过比较不同模型的极大似然值,帮助我们选择能实现最佳拟合效果的协变量的一阶和二阶形式。
ssc install psestimate
psestimate D1 x1 x2 x3
options:
totry(indepvars)//供选择的协变量列表,默认为全部
notry(varlist)//指定不包括的协变量列表,默认为没有
nolin//指定不进行一阶多项式的选择
noquad//指定不进行二项多项式的选择代码举例
psestimate D1 x1, totry(x2 x3 x4 x5 x6) noquad//首先,加入noquad,
只筛选协变量的一阶形式,这样可以提升运算速度
*然后会呈现:
Selected first order covariates are:x2 x3
Final model is: x1 x2 x3将最终选定的x1 x2 x3作为解释变量放入基准模型当中,再加入nolin选项值进行二阶形式的筛选。
psestimate D1 x1 x2 x3,totry(x2 x3 x4 x5 x6)nolin
*Selected second order covariates are:x3#x4
Final model is: x1 x2 x3 x3#x4最后用上述筛选出来的匹配变量进行PSM匹配。
五、PSM方法的stata操作
1. 首先安装外部命令
ssc install psmatch22.样本随机排序
在使用PSM方法之前需要对样本进行随机排序。我们所使用的方法用runiform函数生成均匀分布的随机数ranorder,再使用sort命令使其从小到大依次排列,实现样本的随机排序。
在生成随机数的时候的步骤是,设定抽样种子,使得每次随机抽样的结果一致。若不设定随机种子的话,生成的随机数将无法重现。
set seed 0001
gen ranorder=runiform()
sort ranorder3. 进行样本配对
psmatch2 D1 x1 x2 x3 outcome(y1)logit
ties ate neighbor(1)common caliper(.05) odds
*D1是处理变量:
比如说1代表接受培训,0代表不接受培训
*x1x2x3是协变量,选取来源于文献
*y1是结果变量
*ate是用来同时汇报ATE/ATU和ATT,
若默认则仅报告ATT
*neighbor(1)表示使用一对一近邻匹配
*common表示仅对共同取值范围内的个体进行匹配,
默认对所有的个体进行匹配
*caliper(.05)指定卡尺,括号内必须为正实数。
*ties表示包括了所有倾向得分相同的并列个体,
若默认则按照数据排序选择其中的一个样本匹配4.分析回归结果
通过下表样本的最终匹配结果,我们可以看出,在对照组当中,不在共同取值范围之内(off support)的样本数仅有16个。而在共同取值范围之内的样本数则有1284个。

计算处置效应
其中,ATT、ATU、ATE,ATT表示处理组的平均处理效应,在本例当中就是指接受培训对工资的影响。ATU是指控制组的潜在处理效应,是指没有接受过培训的员工,若接受培训对其的潜在影响。


5.检验匹配后的数据平衡性
pstest命令
用命令pstest来进行平衡性检验,x1x2x3是需要检验的变量,both表示同时显示匹配前的数据平衡情况,默认仅显示匹配后的情况。
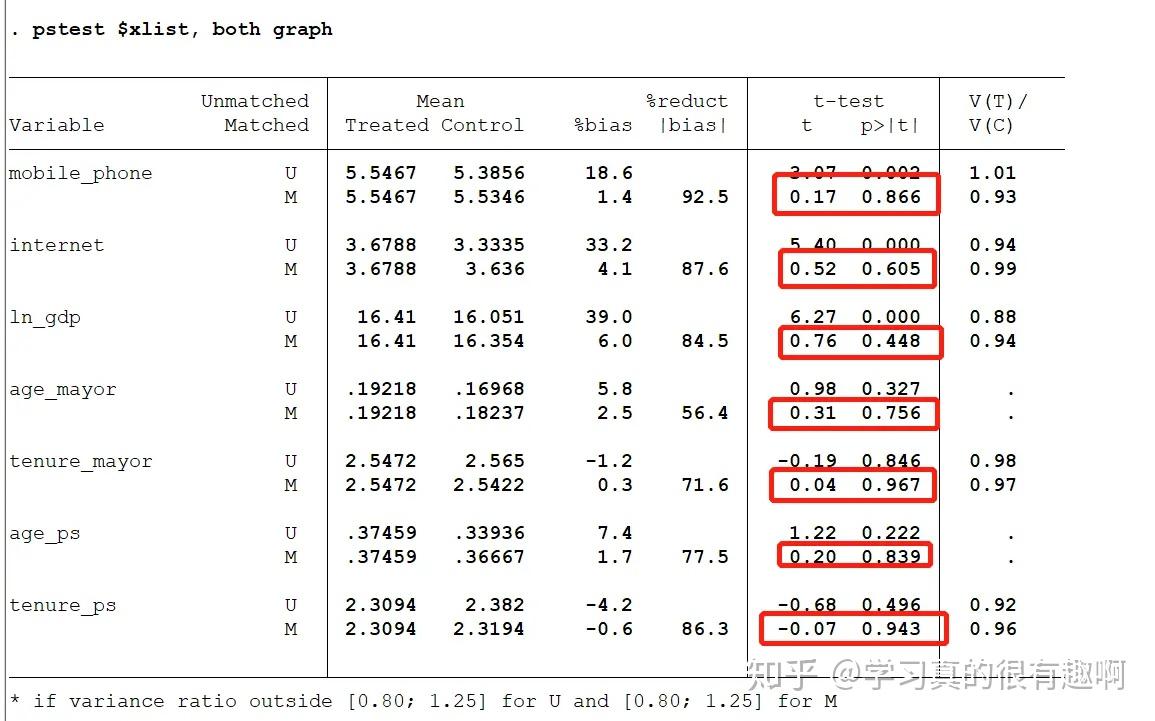
pstest x1 x2 x3,both graph
若在匹配之后数据的标准差明显减少,变得更为集中,那说明匹配的质量较好。
最后我们删除不处于共同取值范围内的样本,off support。若需要也可删除在PSM过程当中生成的变量:drop _*
由下图可见,匹配后的对照组和控制组之间没有显著差异,证明平衡性假设条件满足。
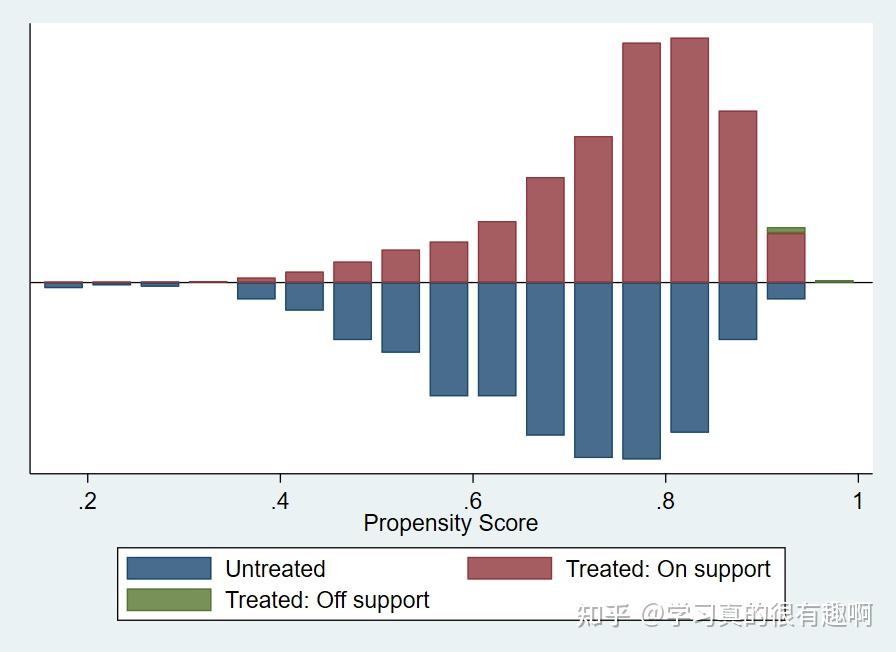
graph表示用图展示变量匹配前后的平衡情况。其中我们可以看到不在共同范围内的样本数量较少,因此在进行匹配的时候,我们损失的样本不多。
核密度图的绘制
比较密度函数图
*-匹配前的密度函数图
twoway (kdensity _ps if _treat==1,lp(solid) lw(*2.5))(kdensity _ps
if _treat==0,lp(dash) lw(*2.5)),ytitle("Density", size(*1.1))
ylabel(,angle(0) labsize(*1.1))
xtitle("Propensity Score", size(*1.1))
xscale(titlegap(2))
xlabel(0(0.2)0.8, format(%2.1f) labsize(*1.1))
legend(label(1 "Treat") label(2 "Control") row(2)
position(3) ring(0) size(*1.1))
scheme(s1mono)
graph export "Fig1.wmf",replace fontface("Times New Roman")
*-匹配后的密度函数图
twoway (kdensity _ps if _treat==1,lp(solid) lw(*2.5))(kdensity _ps
if treat==0 & _wei!=.,lp(dash) lw(*2.5)), ytitle("Density", size(*1.1))
ylabel(,angle(0) labsize(*1.1))
xtitle("Propensity Score", size(*1.1))
