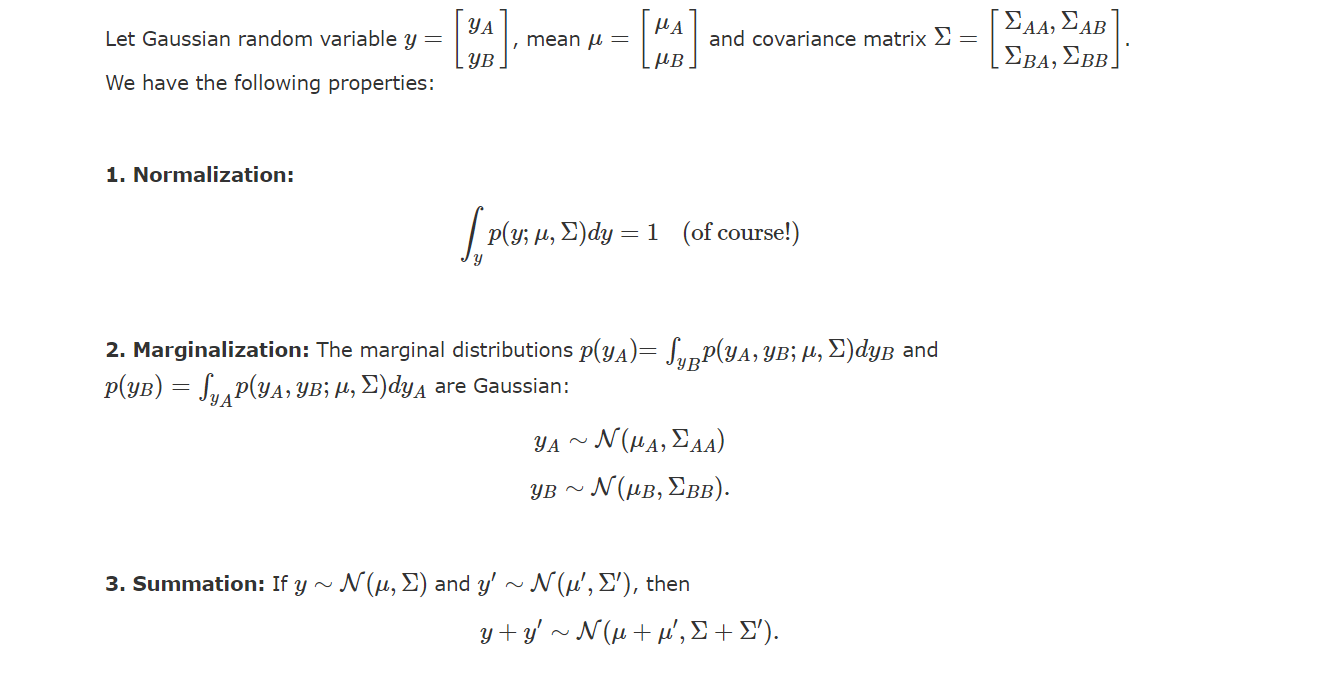考虑一个回归问题:
= \int_{\mathbf{w}} P(Y \mid \mathbf{w}, D,X) P(\mathbf{w} \mid D) d\mathbf{w} \qquad(A-6)
=∫wP(Y∣w,D,X)P(w∣D)dw(A−6)
然而上述公式的解析解(closed form)难以计算,但对于具有高斯似然和先验的特殊情况,我们可以求其高斯过程的均值和协方差,即:
P(y_*\mid D,\mathbf{x}) \sim \mathcal{N}(\mu_{y_*\mid D}, \Sigma_{y_*\mid D}) \qquad(A-7)
P(y∗∣D,x)∼N(μy∗∣D,Σy∗∣D)(A−7)
其中均值函数
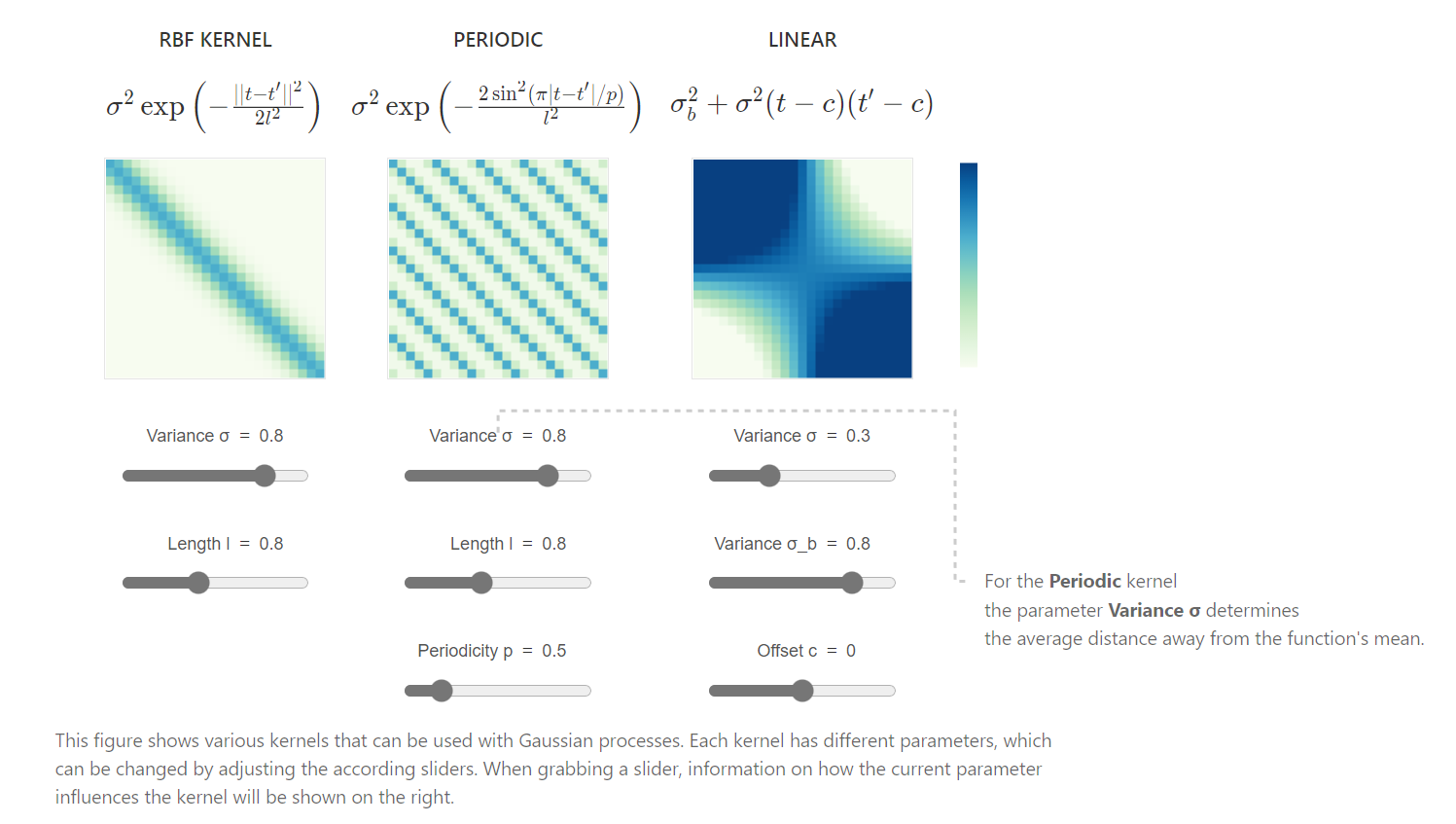
高斯过程回归(Gaussian process regression,GPR)是一个随机过程(按时间或空间索引的随机变量集合),这些随机变量的每个有限集合都服从多元正态分布,即它们的每个有限线性组合都是正态分布。高斯过程的分布是所有这些(无限多)随机变量的联合概率分布。定义:一个高斯过程是一组随机变量的集合,这组随机变量的每个有限子集构成的联合概率分布都服从多元高斯分布,即:f∼GP(μ,k)(1−1)f \sim GP(\mu,k) \qquad(1-1) f∼GP(μ,k)(1−1)其中μ(x)\m
高斯过程回归的和其他回归算法的区别是:一般回归算法给定输入X,希望得到的是对应的Y值,拟合函数可以有多种多样,线性拟合、多项式拟合等等,而高斯回归是要得到函数f(x)的分布,那么是如何实现的呢?
对于数据集,令,从而得到向量, 将所需要预测的的集合定义为,对应的预测值为, 根据贝叶斯公式有:
```python
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
from pyswarm import pso
# 定义高斯过程回归优化目标函数
def gp_regression(x, y):
kernel = C(x[0], (1e-3, 1e3)) * RBF(x[1], (1e-3, 1e3))
gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
gp.fit(X, y)
score = -gp.score(X, y)
return score
# 定义优化的变量范围
x0 = [1.0, 1.0] # 初始值
lb = [0.01, 0.01] # 下界
ub = [100.0, 100.0] # 上界
# 生成随机数据
np.random.seed(1)
X = np.random.uniform(-5.0, 5.0, size=(20, 1))
y = np.sin(X[:, 0])
# 使用粒子群优化算法优化高斯过程回归
xopt, fopt = pso(gp_regression, lb, ub)
print("Optimization results:")
print("xopt: ", xopt)
print("fopt: ", fopt)
在上面的代码中,我们使用 `GaussianProcessRegressor` 类来拟合高斯过程回归模型,并且使用粒子群优化算法 `pso` 函数来优化模型的超参数。`gp_regression` 函数是高斯过程回归的优化目标函数,它的输入是模型超参数的值 `x` 和训练数据 `y`,输出是负对数似然值的相反数(因为我们使用粒子群优化算法最小化目标函数)。
我们设置了初始值 `x0` 和变量范围 `lb` 和 `ub`。然后,我们生成随机数据 `X` 和 `y`,并使用 `pso` 函数来优化高斯过程回归模型的超参数。最后,我们输出优化结果 `xopt` 和 `fopt`,其中 `xopt` 是最优超参数的值,`fopt` 是对应的负对数似然值的相反数。