高等数学日常问题笔记------什么时候使用定义求导数,什么时候直接求导数?

今天在学习高等数学的时候往前回顾了一下,突然发现导数这里出现问题了————什么时候使用定义求导数,什么时候直接求导数?
在回答这个问题之前,我首先给大家几个概念:
导数: 设函数 y=f(x) 在点x0的某个邻域内有定义,当自变量 x 在 x_{0} 处有增量 \Delta x , x_{0}+\Delta x 仍在该邻域内时,相应地因变量取得增量 Δy=f(x_{0}+\Delta x)-f(x_{0}) ;如果 Δy 与 Δx 之比当 Δx→0 时极限存在,则称函数 y=f(x) 在点 x_{0} 处可导,并称这个极限为函数 y=f(x) 在点 x_{0} 处的导数 ,记为 f'(x_{0}) ,即
f'(x_{0})=\lim_{\Delta x \rightarrow 0}{\frac{\Delta y}{\Delta x}}=\lim_{\Delta x \rightarrow 0}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x} 。
导函数: 如果函数 f(x) 在开区间 I 内的 每点处都可导 ,那么就称函数 f(x) 在开区间 I 内可导。这时,对于任一 x\in I ,都对应着 f(x) 的一个确定的导数值,这样就构成了一个新的函数,这个函数叫做原来函数 y = f(x) 的导函数,其中的一种记作方式为: f'(x) 。
从以上两个概念我们不难看出,若是我们求 y = f(x) 在某点处的导数,这时一般选用定义法;如果我们求函数 f(x) 在区间 I 内的导数那我们可以使用公式法直接求导,走到这里是不是就明朗了许多。
这时,又有同学问了,有时候我求函数在某一点的导数的时候我也是直接用的公式法求导的,我也没有用定义,例如求曲线在某一点处切线的斜率,我直接对曲线方程进行求导,然后在把这点的自变量的值带入,然后得出的值就是此时曲线在这点处切线的斜率。
我们先来看看这两个定义,第一个定义我们是 不知道此时的函数是否可导 ,我们需要通过因变量的增量和自变量增量比值的极限值是否存在去判断导数是否存在;而第二个定义我们已经知道了 函数在区间上处处可导 。
重点:也就是说如果我们在已知函数 y = f(x) 在区间内处处可导的前提条件下,让我们去求某一点的导数值或者是去求函数在某一区间上的导数,那我们就可以直接使用公式法去求导数,当然也可以使用定义来求导数。
反之,如果我们不确定 y = f(x) 在区间内是不是处处可导的,那我们就需要使用导数的定义来求导数在某一点处的导数值或者是导数,换句话说就是当题目让你讨论函数在某点的可导性的时候我们需要选用定义法来做题目(因为此时涉及的是“点”)。
也就是说当题目涉及的是:“点”(求在某点处的导数值或者导数)并且不知道函数是否可导的时候我们使用定义法来做;
当我们知道函数在某个区间内处处可导的时候,不论是求导函数,还是求函数在某一点处的导数值我们都可以使用公式法直接求导。
例如,在分段函数中让你判断分段点处是不是可导的这种题目,此时,我们需要在分段函数的分段点处使用定义来求其导数,然后根据导数在某点处可导的充分必要条件:左导数等于右导数来判断分段函数在分段点处是否可导。
例题1:设函数
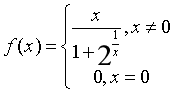
讨论 f(x) 在 x=0 处的可导性。
解析:此题是让我们讨论 f(x) 在分段点 x=0 处是否可导,换句话说就是我们不知道函数在分段点处是否可导且涉及的是点,所以我们需要使用导数的定义来求解。
【答案: f(x) 在 x=0 处连续,但是不可导。】(此处过程省略)
下面我们再来看一个例题
例题2:
设函数
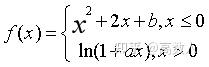
处处可导,确定常数 a,b, 并求 f'(x) 。
解析:此题我们知道 f(x) 是处处可导的,所以在分段点处也是可导的,所以在分段点处也是连续的,由此我们可以确定 b 的值为0,在根据左导数等于右导数确定 a 的值。
此时在分段函数求导的时候我们使用定义求导。
最后得出 a=2,b=0 ,在求 f'(x) 的时候我们直接使用 公式法 就可以了。
总结:
- 在不确定函数在某点是否可导的情况下,不管是让我们求某一点处的函数值还是讨论其在某一点是否可导我们都要使用定义法, 也就是我们拿到题目之后先看看题目中有没有明确告诉我们函数是否是可导的,只要不确定函数可导,有关导数的一切操作我们都要使用定义法;函数已经明确在其区间内处处可导我们就可以使用公式法。
- 像例题2那样我们其实在做有关分段函数在分段点处的导数时我们不需要很麻烦,记住一点就可以了-------- 只要遇到有关分段函数的分段点处的导数问题时我们就选用定义法,这样保准没错; 但是像例题2的第二问那种的我们已经知道函数处处可导了求导数直接就是用公式法就行了。 也就是在分段函数中涉及分段点处的导数问题时我们用定义,其余的告诉处处可导了让我们求分段函数的导数问题的我们使用公式法就可以了


