教资科目三/初中数学/高中数学/学科知识与教学能力/学科知识部分

历年真题试卷 可以下载“粉笔教师APP”，里面有初中数学和高中数学的历年试卷，免费的。还有答案解析。

线性代数和微积分这两部分内容较多而且相对独立，单独做了2个专题，大家可以去专题里看。

学科知识部分，对比考试大纲，初中和高中考试范围基本差不多。初中和高中最大的差别就是最后2道大题，高中的会偏难，教学设计和案例分析都是高中的知识。

初中考试大纲：

学科知识的复习，主要按照以下几个步骤进行： 第一，概念/定义。第二，运算法则/定理/推理。第三，几何表示/数形结合/图像及性质。第四，计算/应用。 基本上每一个板块都是按照这个思路下来。下面的复习会按知识点的由易到难展开。

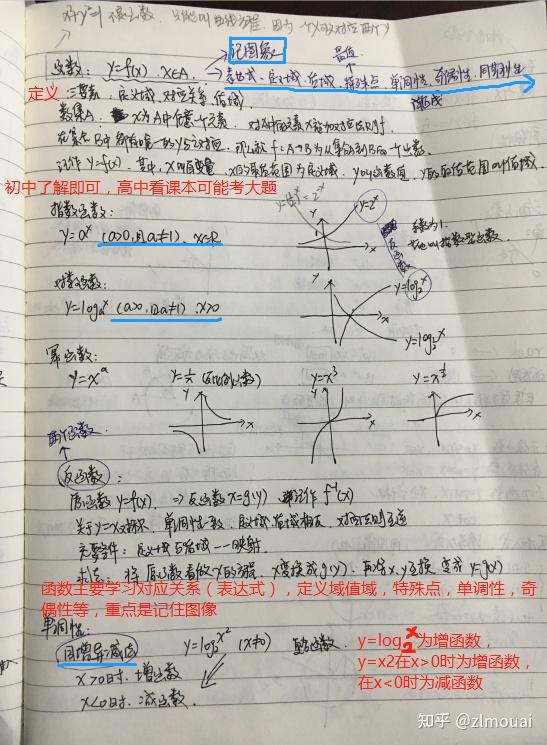
上面的都是不怎么考的，但是需要了解。下面要讲的都是考试的重点。

平面与平面的位置关系，就是看两个法向量的位置关系；第二个平面法向量就是ABC系数，n2（1/2，2，-7）。第一个平面π法向量垂直平面内任一向量，用平面内2个向量的叉乘求出法向量。求与平面π垂直的平面π1，可以取p1p2作为π1的法向量（平面垂直也就是法向量垂直），用点法式来求。

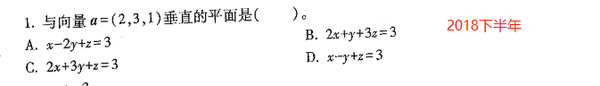
向量垂直平面，表示该向量是法向量。取ABC系数，答案为c

两直线的位置关系，看方向向量。交面式的表达式，两个平面确定一条直线，用平面的法向量的叉乘求出直线方向向量，平面的法向量取系数ABC

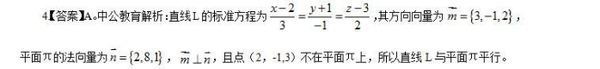
椭圆：（结合上面的图形）

第一定义，固定两点，用一个长度固定的线系在这两点，用笔将线拉直作图得到椭圆。

定点F1，F2叫焦点，定长度PF1+PF2=2a，F1F2=2c叫焦距。OF1=OF2=c.

三角形两边之和大于第三边，2a>2c ，得出a>c / 或者从图像上x轴可以直接看出

记一个等式，b2=a2-c2

长轴与短轴：焦点在x轴上时，x轴为长轴，x轴的截距为a比y轴的截距b长。即上图。

焦点在y轴上时，y轴为长轴，y轴的截距为a比x轴的截距b长，表达式为y2/a2+x2/b2=1

双曲线：

第一定义，定点F1,F2，点p到两定点的距离差等于定值，即|PF1-PF2|=2a，两边之差小于第三边，2a<2c , a<c。b2=c2-a2

抛物线：

动点p到定点F和定直线l的距离相等

2，是个等式的变形题（计算化简题），不需要用到空间几何的知识。还运用了三角函数倍角公式。

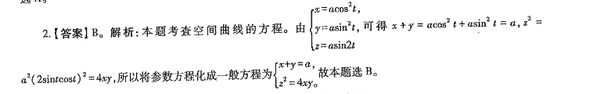
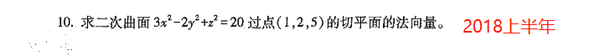
这道题涉及条件概率。先说独立事件概率。两个事件A与B是相互独立的,则P(AB)=P(A)P(B),那么A在B这个前提下的条件概率就是A自身的概率。条件概率是指 事件A 在另外一个 事件B已经发生条件下 的发生概率。条件概率表示为：P（A|B），读作“在B的条件下A的概率”。

这种题目怎么解？看题目应该知道是条件概率的考察，某考生通过了考试的情况下，该考生是本专业的概率。在B发生的条件下，A发生的概率。

第一步 ， 先找出两个事件A和B 。A=考生是本专业，B=考生通过了考试。结果要求P（A|B）

第二步 ， 把题目中已知的概率用符号表示出来 。60%是本专业，即 P(A) =0.6。 40%是非本专业，即 P(Ā） =0.4，本专业考生的通过率85%，即考生是本专业的情况下，通过考试概率是85%，即 P（B|A) =0.85。非本专业考生通过率50%。即考生是非本专业的情况下，通过考试概率是50%，即 P（B|Ā) =0.5。

第三步 ， 运用公式求解 。P(A|B)=P(AB)/P(B)。分母P(AB)可以用已知条件中P(A)与P（B|A)相乘得出。分子P(B)可以用全概率公式，P(B)=P(AB)+P(ĀB），P(AB)上面已求出，P(ĀB）可以用已知条件P(Ā）和P（B|Ā)相乘得出。最后代入

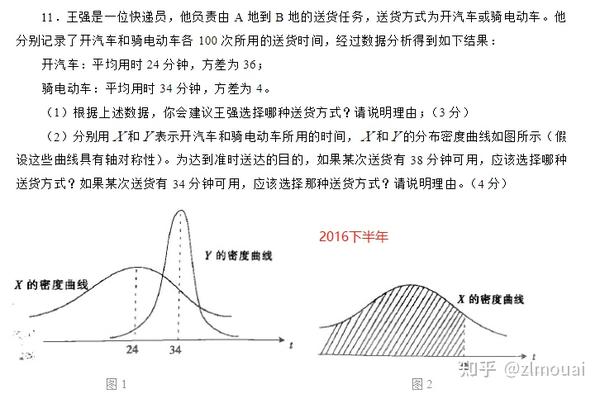
未完待续。。。