1.协方差矩阵的概念:
这里在讲述
协方差矩阵
的性质之前先讲解一下协方差、方差以及两者之间的关系【统计学中的样本方差、样本均值看我的另外一篇文章{
浅谈均值、方差、标准差、协方差的概念及意义
}】
一:方差:描述的是样本集合的各个样本点到均值的距离之平均,一般是用来描述一维数据的。
方差是用来衡量单个变量“自身变异”大小的总体参数,方差越大表明该变量的变异越大。
二:协方差是用来衡量两个变量之间“协同变异大小的总体参数,即二个变量相互影响的大小的参数,协方差的绝对值越大,则两个变量相互影响越大。”
协方差的性质:①. 是一种用来衡量两个随机变量 关系的统计量。②. 只能处理二维问题。③. 计算协方差需要计算均值。
如下式: 定义 量E{[X-E(X)] [Y-E(Y)]}称为随机变量X和Y的协方差。记为Cov(X,Y),即
Cov(X,Y)
=E{[X-E(X)] [Y-E(Y)]}而
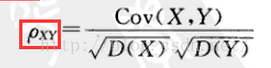 称为随机变量X和Y的相关系数。
称为随机变量X和Y的相关系数。
当上式结果为正时表示随机变量X和Y正相关,为负值是表示随机变量X和Y为负相关,结果为0表示两者相互独立,无关。
三:方差与协方差的关系
Cov(X,Y)
=
Cov(
Y
,
X
)
;
Cov(X,
X
)
=D(X).
对任意两个随机变量X和Y,下列等式成立:D(X+Y)=D(X)+D(Y)+2
Cov(X,Y)
。
将
Cov(X,Y)
的定义式展开,易得
Cov(X,Y)
=E(XY)-E(X)E(Y)
2.协方差矩阵的性质:
①. 协方差矩阵能处理多维问题;
②. 协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差;
③. 协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的;
④. 样本矩阵中若每行是一个样本,则每列为一个维度,所以计算协方差时要按照列计算均值。
如果数据是3维的,那么协方差矩阵是:
由性质④可知:
详细实例请看连接文章:http://blog.csdn.net/ybdesire/article/details/6270328/
协方差(i,j)=(第 i 列所有元素中每个元素都 - 第 i 列均值)*(第 j 列所有元素 - 第 j 列均值)
协方差的matlab计算公式则为:协方差(i,j)=(第 i 列所有元素中每个元素都 - 第 i 列均值)*(第 j 列所有元素 - 第 j 列均值)/(样本数-1)
3.矩阵特征值、特征向量以及局部坐标系之间的关系
关于特征值及特征向量的相关概念参考线性代数有关知识点:这里先来了解两个定理:
定理1:设r1、r2、...rm是方阵A的m个特征值,p1、p2、...pm依次是与之对应的特征向量,如果r1、r2、...rm各不相等,则p1、p2、...pm线性无关。
定理2:设r1、r2是对称矩阵A的两个特征值,p1、p2是对应的特征向量,若r1与r2不想等,则p1和p2正交。
线性变化:
线性变换
(线性映射)是在作用于
两个向量空间之间的函数
,它保持
向量加法和标量乘法
的运算,从一个向量空间变化到另一个向量空间。
实际上线性变换表现出来的就是一个
矩阵
。
特征值和特征向量
是一体的概念:
对于一个给定的
线性变换(矩阵A)
,它的
特征向量
ξ
经过这个线性变换之后,得到的新向量仍然与原来的
ξ
保持在同一條直線上
,但其
长度也许會改变
。一个特征向量的长度在该线性变换下
缩放的比例(λ)称为其特征值
(本征值)。
数学描述:
A
ξ
=
λ
ξ
在线性变换
A
的作用下,向量
ξ
仅仅在尺度上变为原来的
λ
倍。称
ξ
是线性变换
A
的一个特征向量,
λ
是对应的特征值。
-
矩阵是一个表示二维空间的数组,矩阵可以看做是一个变换。在线性代数中,矩阵可以把一个向量变换到另一个位置,或者说从一个坐标系变换到另一个坐标系。矩阵的“基”,实际就是变换时所用的坐标系。
-
矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
-
任意给定一个矩阵A,并不是对所有的向量x它都能拉长(缩短)。凡是能被矩阵A拉长(缩短)的向量就称为矩阵A的特征向量(Eigenvector);拉长(缩短)的量就是这个特征向量对应的特征值(Eigenvalue)。
-
一个矩阵可能可以拉长(缩短)多个向量,因此它就可能有多个特征值。
-
对于实对称矩阵来说,不同特征值对应的特征向量必定正交。
-
一个变换矩阵的所有特征向量组成了这个变换矩阵的
一组基
。所谓
基,可以理解为坐标系的轴
。我们平常用到的大多是直角坐标系,在线性代数中可以把这个坐标系扭曲、拉伸、旋转,称为
基变换
。我们可以按需求去设定基,但是基的轴之间必须是线性无关的,也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成,否则的话原来的空间就“撑”不起来了。在主成分分析(PCA)中,我们通过在拉伸最大的方向设置基,忽略一些小的量,可以极大的压缩数据而减小失真。
-
变换矩阵的所有特征向量作为空间的基之所以重要,是因为在这些方向上变换矩阵可以拉伸向量而不必扭曲它,使得计算大为简单。因此特征值固然重要,但我们的终极目标却是特征向量。
-
同一特征值的任意多个特征向量的线性组合仍然是A属于同一特征值的特征向量。
顾名思义,特征值和特征向量表达了一个线性变换的特征。在物理意义上,一个高维空间的线性变换可以想象是在对一个向量在各个方向上进行了不同程度的变换,而
特征向量之间是线性无关
的,它们对应了最主要的
变换方向
,同时特征值表达了相应的
变换程度
。
具体的说,求特征向量,就是
把矩阵A所代表的空间进行正交分解
,使得A的向量集合可以表示为每个向量a在各个特征向量上的投影长度。我们通常求特征值和特征向量即为求出这个矩阵能使哪些向量
只发生拉伸,而方向不发生变化
,观察其发生拉伸的程度。这样做的意义在于,看清一个矩阵在哪些方面能产生
最大的分散度
(scatter),减少重叠,意味着更多的信息被保留下来。
在概率论和
统计学
中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为E(X) = μ 与 E(Y) = ν 的两个实数随机变量X与Y之间的协方差定义为:
COV(X,Y)=E[(X-E(X))(Y-E(Y))],其中,E是期望值。
它也可以表示为:直观上来看,协方差表示的是两个
X、Y是一个列向量,它表示了每种情况下每个样本可能出现的数。比如给定
则X表示x轴可能出现的数,Y表示y轴可能出现的。注意这里是关键,给定了4个样本,每个样本都是二维的,所以只可能有X和Y两种维度。所以
这里只有X,Y两列,所以得到的
协方差矩阵
是2x2的
矩阵
,分别计算
协方差矩阵
的各个元素
在概率论中,两个随机变量 X 与 Y 之间相互关系,大致有下列3种情况:情况一,如上, 当 X, Y 的联合分布像上图那样时,我们可以看出,大致上有: X 越大 Y 也越大, X 越小 Y 也越小,这种情况,我们称为“正
相关
”。情况二, 如上图, 当X, Y 的联合分布像上图那样时,我们可以看出,大致上有:X 越大Y 反而越小,X 越小 Y 反而越大,这种情况,我们称为“负
相关
”。情况三,如上图,...
本篇笔记将以向量值随机变量X=(X1,…,Xn)TX=(X_1,\dots,X_n)^TX=(X1,…,Xn)T的
协方差矩阵
为例,研究其
性质
。在阅读笔记之前可先记下先导篇中的
相关
结论,尤其是该篇中任意方向发散程度章节的结论。本篇笔记主要参考借鉴的基础教材是《程序员的数学之概率统计》。
单位
矩阵
与圆
首先看一种最简单的情况,即
协方差矩阵
为单位
矩阵
。此时该
矩阵
有一个显著特征,即任意方向上的方差都为...
协方差矩阵
的
意义
:
方差是变量减均值的期望,两个变量的协方差是变量一减均值,乘以,变量二减均值,的期望。
协方差矩阵
,就是多个变量两两间协方差值,按顺序排成的
矩阵
。协方差的
意义
是,衡量两个变量偏差变化趋势是否一致,除以两变量标准差之积以标准化,即
相关
系数
对于机器学习领域的PCA来说,如果遇到的
矩阵
不是方阵,需要计算他的
协方差矩阵
来进行下一步计算,因为
协方差矩阵
一定是方阵,而特征值分解针对的必须...
$$\mathbf{X}=(X_1,X_2,...,X_n)^T$$
两个随机向量的协方差:
cov[Xi,Xj]=E[(Xi−E[Xi])(Xj−E[Xj])]cov[X_i,X_j]=E[(X_i-E[X_i])(X_j-E[X_j])]cov[Xi,Xj]=E[(Xi−...
X¯=1n∑i=1nXiX¯=1n∑i=1nXi\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}
S=D(X)=1n∑i=1n(Xi−X¯)2S=D(X)=1n∑i=1n(Xi−X¯)2S=D(...
均值描述的是样本集合的中间点,它告诉我们的信息是有限的,而标准差描述的是样本集合的各个样本点到均值的距离之平均。
之所以除以n-1而不是n,是因为这样能使我们以较小的样本集更好地逼近总体的标准差,即统计上所谓的“无偏估计”
协方差矩阵
对学统计的来说很重要,本文详细说明其
相关
知识(计算公式等)以及来历与实质含义。其实质主要是从一维到多维的一个推广。从以下几个点去描述它的来历:
一、低维样本情形的统计量:均值、标准差、方差
二、高维样本情形的统计量::均值、协方差
一、低维情形的统计量:均值、标准差、方差
假设自然数集中抽取一个含有3个样本的集合 :=(1,2,3), 我们简记这个集合的一些统计
概念
: 均值:,方差:,标准差:(), 依次给出这些
概念
的公式描述。
均值一般指平均数。平均数,
统计学
术语,是表...
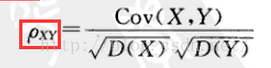 称为随机变量X和Y的相关系数。
称为随机变量X和Y的相关系数。