黎曼几何与流形学习
1、基础概念介绍
在获取全局的几何特征时,传统的数据分析一般会导致失败。其原因在于空间本质上是 全局线性 的,而数据本身往往呈现出 强非线性特征 。这时可以借助流形,在欧氏空间中嵌入非欧式低维流形。从几何的角度来看,流形本质上反映了 全局 与 局部 属性的区别和联系。
定义一个空间以及在该空间中的度量,使得在无穷小的范围内与欧式空间相同,即在每一个无限小的区域内,欧式空间的几何关系成立。这个空间就可以被看作 黎曼空间 ,空间中的几何叫做 黎曼几何 。因此,可以说黎曼空间是在 无限小 范围内的欧式空间。
1.1 流形(manifold)
流形是局部具有欧几里得空间性质的空间,是高维空间中曲线、曲面概念的拓广。我们可以在低维上直观理解这个概念,比如我们说三维空间中的一个曲面是一个二维流形,因为它的本质维度(intrinsic dimension)只有2,一个点在这个二维流形上移动只有两个方向的自由度。同理,三维空间或者二维空间中的一条曲线都是一个一维流形。欧几里得空间就是最简单的流形的实例。
其数学定义为:令M表示一个拓扑空间,对于其上的任意一点 m\in M ,都存在 m 的一个开邻域 \Omega 和 d 维欧式空间中的一个开子集同胚,则把 M 称为 d 维拓扑流形,也叫做 d 维流形。
1.2黎曼几何(Riemannian geometry)
微分几何中,黎曼几何研究具有 黎曼度量 的光滑 流形 ,即流形切空间上二次形式的选择。它特别关注于角度、弧线长度及体积。把每个微小部分加起来而得出整体的数量。
19世纪, 波恩哈德·黎曼 把这个概念加以推广。任意平滑流形容许 黎曼度量 及这个额外结构帮助解决微分拓扑问题。它成为 伪黎曼流形 复杂结构的入门。其中大部分都是 广义相对论 的四维研究对象。 [1]
1.3黎曼流形(Riemannian manifold)
黎曼流形或是黎曼空间是指在流形 M 上任意一点的切空间 T_{m}M 处定义了欧式内积的平滑微分流形。具体来说:
黎曼流形是一个 微分流形 ,其中每点p的 切空间 都定义了 点积 ,而且其数值随p平滑地改变。它容许我们定义弧线长度、角度、面积、体积、 曲率 、函数 梯度 及 向量域 的 散度 。
每个 R_n 的平滑 子流形 可以导出 黎曼度量 :把 R_n 的 点积 都限制于 切空间 内。实际上,根据 纳什嵌入定理 ,所有黎曼流形都可以这样产生。
我们可以定义黎曼流形为和 R_n 的平滑子流形是 等距同构 的 度量空间 , 等距 是指其 内蕴度量 (intrinsic metric)和上述从 R_n 导出的度量是相同的。这对建立 黎曼几何 是很有用的。
黎曼流形可以定义为平滑流形,其中给出了一个 切丛 的正定二次形的光滑截面。它可产生度量空间:
如果 \gamma : [ a , b ] → M 是黎曼流形 M 中一段连续可微分的弧线,我们可以定义它的长度 L(\gamma) 为
\\L(\gamma) = \int_{a}^{b}\left| \gamma'(t) \right|dt
(注意: \gamma'(t) 是切空间 M 在 \gamma'(t) 点的元素;|·|是切空间的内积所得出的 范数 。)
使用这个长度的定义,每个 连通 的黎曼流形 M 很自然的成为一个 度量空间 (甚至是 长度度量空间 ):在 x 与 y 两点之间的距离 d ( x , y )定义为:
d ( x , y ) = inf { L(\gamma) : \gamma 是连接 x 和 y 的一条光滑曲线}。
虽然黎曼流形通常是弯曲的,“直线”的概念依然存在:那就是 测地线 。
在黎曼流形中, 测地线 完备 的概念,和 拓扑 完备及 度量 完备是等价的:每个完备性都可以推出其他的完备性,这就是 Hopf-Rinow定理 的内容。 [1]
常见的黎曼流形可以分为SPD流形、Grassmann流形以及Stiefel流形。
1.3.1 Stiefel流形
把一组尺寸为 d\times q 的矩阵表示为: R^{d\times q} ,其是一个向量空间,同时该空间具有一个线性流形结构,可表示为: \varphi:R^{ d\times q} \rightarrow R^{dq}:Y\rightarrow vec(Y) ,其中 vec(Y) 表示将Y的所有列堆叠在一起而得到的向量,通过在该线性流形中利用元素的内积,就可以把流形映射到一个欧式空间:
\\ <Y_{1}, Y_{2}>:=vec(Y_{1})^{T}vec(Y_{2})=tr(Y_{1}^{T} Y_{2})
同样的,用 R_{\phi}^{d\times q} (q\leq d) 表示一组尺寸都为 d\times q 且所有列都是线性无关的矩阵,相对于 R^{d\times q} , R_{\phi}^{d\times q} (q\leq d) 则是其的一个开集,且 X\in R^{d\times q} :det(Y_{T}Y)=0 。很显然,由 R_{\phi}^{d\times q} 所张成的空间是关于 R^{d\times q} 的一个开子流形。其微分结构可以表示为: \varphi:R_\varphi ^ {d\times q} \rightarrow R^{d\times q}:X \rightarrow vec(X) 。对于 R_{\phi}^{d\times q} 中的任一元素,其所有的列都是正交基向量,因此可得:
\\ St(q,d):=\left\{ Y\in R^{d\times q} : Y^T Y=I_q\right\}
其中 I_q 是一个 q\times q 的单位矩阵,我们把 St(q, d) 叫做Stiefel流形。
1.3.2 Grassmann流形
令 Grass(q,d) 表示一组q维的子控件,其中 q\leq d , Stirefel流形是由一组尺寸为 d\times q 的列满秩矩阵构成的,用 \sim 表示 R_{\phi}^{d\times q} 上的一个等价关系:
\\ Y_i \sim Y_j \Leftrightarrow span(Y_i) =span(Y_j)
其中,span(Y)表示由 Y\in R_\varphi ^{d\times q} 的所有列张成的子空间。
简单的说,在一个d维的向量空间W,W中取q维子空间,就构成了Grassmann流形。
1.3.3 SPD流形
令 Symx_{\phi}^{d} 表示 d\times d 的对称正定矩阵所处的空间,对任意两个处于其上的数据 C_{1}, C_{2} \in Symx_{\phi}^{d} ,他们的对数积可表示为:
\\ C_{1} \odot C_{2} :=exp(log(C_{1}) + log(C_{2}))
(Symx_{\phi}^{d}, \odot) 是一个群。同时,对于任意两个SPD矩阵,它们之间对数积等价于两个矩阵的积。而且该积是可交换的。因为,任意两个SPD矩阵的乘积是通过在矩阵的对数中定义加法操作而完成的,因此其满足关联性和交换性。当 [C_{1}\cdot C_{2}] =0 时:
\\ exp(log(C_{1}) + log(C_{2})) = exp(log(C_{1}) \cdot log(C_{2})) = C_{1}\cdot C_{2}
Symx_{\phi}^{d} 中的对数积 \odot 与平滑的流形结构是相互兼容的,因此,在 Symx_{\phi}^{d} 中通过利用 \odot 操作可以构建一个交替的李群结构,这里 Symx_{\phi}^{d} 就是一个李群,即SPD流形。
1.4 黎曼度量(Metric tensor)
黎曼流形作为一个几何概念有很多实际应用。一些物理和技术系统的问题都可以表示为黎曼流形问题。 比如,将惯量矩阵看作黎曼度量,力学中的拉格朗日方程就可以表示为黎曼流形,而方程的解就是黎曼流形上的测地线(测地线定义为曲面上最短的一条曲线)。机械动力系统可以用拉格朗日方程表示。在系统中引进控制量,就变为控制系统问题。这种控制系统问题可以转换为黎曼流形问题,即微分几何控制问题。 [2]
2、背景介绍
假设观测数据是均匀采样与高维欧式空间的低维流形,流形学习就是从高维观测数据中发现低维流形结构,并给出从 高维 空间 到低维 嵌入的 映射 。其主要目的就是从期望寻找产生数据集的内在规律性,即从观测数据中寻找数据本质特征,从统计角度看,流形学习是试图去除更多的先验假设,如属性间的相互独立、近正态分布等等,而去完成在一般意义下针对数据集的各项任务。
从模式识别的角度来看,主要存在以下 两个 问题:
- 如何由现有数据中提取高效、信息丰富的特征;
- 如何针对识别的任务设计合理有效的分类算法或是任务。
在统计模型趋于成熟的大背景下,目前一些传统的统计模型如线性子控件、协方差矩阵和高斯概率模型等,可以有效地完成识别的任务,但是这些统计模型通常位于一个特定的黎曼流形上,因此传统的黎曼度量学习方法虽然可以为这一问题提供有效地判别学习方法。
流形学习的主要目的就是在高维数据集中寻找出低维的本质特征的描述,从而找出数据内在的关系,完成特征提取或是模式识别等任务。流形学习与其他领域的关系见下图。
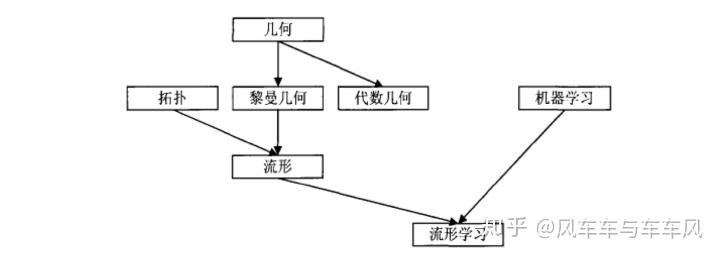
3、流形学习算法
传统的降维算法主要包括PCA, LDA, ICA, FA等,他们主要研究在高维空间中如何设计线性模型的特征向量,优点是运算简便面具有解析的映射函数,但是在现实生活中高维数据大多是非线性的,线性方法很难挖掘高维数据的几何结构和相关性,揭示其流形分布。针对高维数据的非线性特征,近年来发展了很多非线性的降维方法,包括子控件方法、神经网络法、遗传算法以及流型学习等。
有时间继续更新算法相关方法。另,附上两篇优秀的参考文章:
流形学习的思考
流形学习的 优点 是在认知、机器学习方面都有很好的可解释性,但是摩尔定律和深度学习的出现对很多领域的方法的冲击是颠覆性的,以至于大家在构建模型时,更多的是关心性能与表现。所以,无论是学术界还是产业界都把精力放到如何优化深度学习模型的结构和参数优化方面,而端到端的建模方式也使我们不再聚焦特征空间内部究竟发生了什么 [3] 。但是流形学习与深度学习、机器学习的结合,依然是个研究热点。


