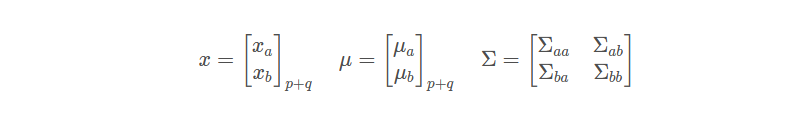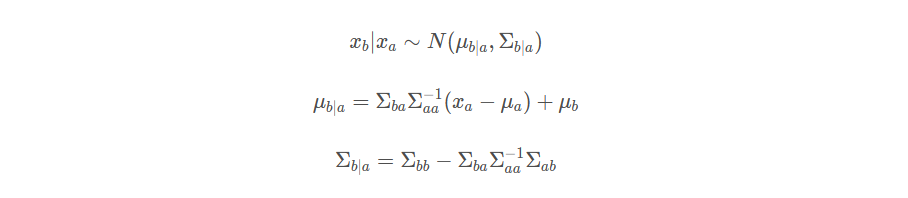概念回顾:
-
中心极限定理:
在适当的条件下,大量相互独立随机变量的均值收敛于正态分布。例如我们要计算全中国人的平均身高。如果每次取10000个身高作为样本,对应有一个样本均值。如果再从总体中重复抽取
n
增大,把所有样本均值记录下来,得到的就是一个接近正太分布的曲线。
-
大数定理:
取样数趋近无穷时,样本的平均值按概率收敛于期望值。比如抛硬币的次数越多,统计结果越接近正反面朝上各一半。
大数定律讲的是样本均值收敛到总体均值(就是期望);
中心极限定理告诉我们,不管总体的分布是什么,总体的任意一个样本均值都围绕在总体均值周围,并呈现正态分布。
-
标准差(standard deviation)与标准误差(standard error):
标准差 = 一次抽样中个体分数间的离散程度,反映了个体分数对样本均值的代表性,用于描述统计。
标准误差 =
多次抽样
中
样本均值
间的离散程度,反映了样本均值对总体均值的代表性,用于推论统计。
点估计:用样本统计量来估计总体参数,因为样本统计量为数轴上某一点值,估计的结果也以一个点的数值表示,所以称为点估计。点估计虽然给出了未知参数的估计值,但是未给出估计值的可靠程度,即估计值偏离未知参数真实值的程度。
区间估计:给定置信水平,根据估计值确定真实值可能出现的区间范围,该区间通常以估计值为中心,该区间被称为为置信区间。
比如:有一个零部件的长度
θ
有95%的概率在(8.7cm,9.2cm)之间,这样描述该长度会更合理。其中(8.7cm,9.2cm)我们就可以理解成置信区间,那么95%就是置信水平。

由样本统计量所构造的总体参数的估计区间为置信区间。由于统计学家在某种程度上确定这个区间会包含真正的总体参数,所以取名置信区间。在统计中,一个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信区间给出的被测量参数的测量值的可信程度,即前面所要求的"一定概率"。这个概率被称为置信水平。
例如:想了解全国成年男性平均身高,可用抽样的方法,用样本信息估计总体信息。从全国男性中抽取一组样本,将这组样本的平均值作为对总体平均值的一个点估计,当有多组样本,即有多组点估计,但我们不知道哪组样本对总体的估计最正确,所以用区间估计来解决这个问题。假设全国成年男性平均身高在165-175cm之间,这个区间叫置信区间,即:[165,175],这个区间的可信程度由置信水平来表现,置信水平指置信区间包含总体平均值的概率多大,如置信水平为95%。

结合中心极限定理,各组样本均值的分布可以用正态分布来近似,总体均值为
目录高斯过程概述高斯过程举例高斯过程的要素与描述径向基函数演示高斯过程回归高斯过程回归的演示高斯过程概述高斯过程从字面上看,分为两部分:高斯:高斯分布;过程:随机过程;当随机变量是一维随机变量的时候,则对应一维高斯分布,概率密度函数p(x)=N(μ,σ2)p(x)=N(\mu,\sigma^{2})p(x)=N(μ,σ2),当随机变量上升至ppp维后,对应高维高斯分布,概率密度函数p(x)=N(μ,Σp×p)p(x)=N(\mu,\Sigma_{p\times p})p(x)=N(μ,Σp×p
写这篇文章的目的就是为了总结一下最近在学习的
高斯
过程
的一些内容,但是由于我是初学者可能有些地方理解不到位,请大家多多谅解~文末附上了一些数学方面的推导。
1.
高斯
过程
定义
高斯
过程
是在连续域上定义的一种随机
过程
,可以看成连续域中所有随机变量的一组集合,并且任意单个或多个随机变量均满足一维
高斯
分布或者多维
高斯
分布。
一个
高斯
过程
可以由一个均值函数以及一个协方差函数(也叫ke...
高斯
过程
是定义在y上的
高斯
分布。
高斯
过程
与核函数紧密相连,定义在y上的
高斯
分布正是通过核函数表示出来的。与线性回归相比,
高斯
过程
没有建立y和x的直接关系,而是通过核函数的方式直接建立y之间的关系。在线性回归模型中,我们假设某个y的取值服从一个
高斯
分布,即y的均值是参数w的一个线性关系,和之间的关系通过w的协方差表现出来。如果给定一个先验,那么可以计算出y的协方差矩阵,如下:
文章目录补充 矩阵求导的重要性质n维正态分布特征函数回顾特征例边际分布的数字特征均值为0的随机变量的数字特征性质边缘分布独立等价于不相关一维正态分布和多维正态分布之间的关联多维正态变量的线性变换不变性补充
在笔记2中实际上已经写过了,但是觉得很重要 就单独再拎出来,也再补充点
补充 矩阵求导的重要性质
n维正态分布
n维正态函数的特征函数 要记住
简易推导:
写成这样(方便后...
高斯
过程
(Gaussian Processes, GP)是概率论和数理统计中随机
过程
的一种,是多元
高斯
分布的扩展,被应用于机器学习、信号处理等领域。博主在阅读了数篇文章和博客后才算是基本搞懂了GP的原理,特此记录。本文目前暂对
高斯
过程
的公式推导和
高斯
过程
回归原理及其优缺点进行讲解和阐述,后续根据个人学习进度再更新源码等内容。
一、一维
高斯
分布
我们从最简单最常见的一维
高斯
分布开始。
众所周知,一维
高斯
分布,又叫一维正态分布的概率密度函数为:
式中,表示均值,表示方差,均值和方差唯一的决定了曲线的
随机
过程
包含平稳
过程
,随机
过程
可以用分布函数和概率密度函数描述,但是比较复杂,所以我们可以用均值和方差描述随机
过程
,而平稳
过程
包含严平稳
过程
,而平稳
过程
满足一定的条件就具有各态历经性
高斯
过程
:随机
过程
kesei(t)的任意n维分布服从正态分布,则称它为
高斯
过程
,也就是说自变量满足正态分布。
高斯
分布不一定是平稳分布,要判断
高斯
过程
是不是平稳
过程
,还要判断一维和二维,和之前判断一样的。
书上44页有...
1,为什么要学习
高斯
过程
.
首先:随机扩散问题.
一根很细的管子,管子宽度可以忽略不记,那么就可以看成一条直线,我们在这条直线某一位置滴一滴墨水,看墨水在水中扩散所造成的影响.
如,给定一个时间t,看墨水扩散的距离,结果是随机的,没有一个确定的答案.我们希望建立起分布.
这个概率分布我们用ρ(y)来表示,表示在时间t内,扩散距离y的概率.ρ(y)是一个概率密度.
然后我们进一步,假设ρ(y)关于原点对称.
关于原点对称我们就得到了期望为0,二阶矩为常数.
t表示任意时间,x表示任意位置,那么f(0,0
高斯
过程
回归(Gaussian Process Regression, GPR)是一种基于贝叶斯学派的非参数回归方法。其基本思想是使用
高斯
过程
(Gaussian Process, GP)对函数进行建模,通过训练数据对函数进行学习和预测。以下是
高斯
过程
回归的一些基本概念:
1.
高斯
过程
:
高斯
过程
是一种随机
过程
,可以用来描述一个随机函数。
高斯
过程
是由一个均值函数和一个协方差函数定义的。
2.
高斯
分布:
高斯
过程
中的随机函数是一个随机变量,其分布满足
高斯
分布,也称为正态分布。
3. 均值函数:
高斯
过程
中的均值函数定义了随机函数的平均值,通常假设为0。
4. 协方差函数:
高斯
过程
中的协方差函数定义了随机函数的相关性质,即相邻点之间的相关程度。通常使用一个核函数来定义协方差函数。
5. 超参数:
高斯
过程
回归中的超参数是指均值函数和协方差函数中的参数。这些参数需要通过最大似然估计或者贝叶斯推断等方法来进行估计。
6. 后验分布:通过训练数据和
高斯
过程
,可以得到一个后验分布,表示对函数的预测结果和不确定性。
7. 预测:
高斯
过程
回归的预测结果是一个
高斯
分布,包括均值和方差。均值表示预测结果,方差表示不确定性。
高斯
过程
回归能够有效地处理高维数据和非线性问题,并且能够提供对预测的不确定性估计。通过使用不同的核函数和超参数,可以对函数的不同性质进行建模。