HDLBits: 在线学习 SystemVerilog(十三)-Problem 72-79(卡诺图)
HDLBits 是一组小型电路设计习题集,使用 Verilog/SystemVerilog 硬件描述语言 (HDL) 练习数字硬件设计~
网址如下:
https:// hdlbits.01xz.net/
关于HDLBits的Verilog实现可以查看下面专栏:
https://www. zhihu.com/column/c_1131 528588117385216
缩略词索引:
- SV:SystemVerilog
从今天开始新的一章-Circuits,包括基本逻辑电路、时序电路、组合电路等。
今天更新整个关于卡诺图部分,数电忘记的,可以先回顾一下。
卡诺图
简介
卡诺图(KM或K -map)是一种简化布尔代数表达式的方法。Maurice Karnaugh在 1953年为Edward W. Veitch 1952 Veitch 图做了改进,并介绍了新的Marquand 图,即我们现在熟知的卡诺图。
卡诺图利用人类的模式识别能力减少了对大量计算的需求,还允许快速识别和消除潜在的竞争条件。
所需的布尔结果从真值表转移到二维网格中,在卡诺图中,单元格按格雷码排序,每个单元格位置代表输入条件的一种组合。单元格也称为最小项,而每个单元格值代表布尔函数的相应输出值。识别出最佳的 1 或 0 组,它们表示原始真值表中逻辑的规范形式的项。这些术语可用于编写表示所需逻辑的最小布尔表达式。
示例
卡诺图用于简化布尔代数函数。例如,考虑以下真值表描述的布尔函数。
函数的真值表
| 序号 | A | B | C | D | f(A,B,C,D) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 0 |
以下是使用布尔变量A、B、C、D描述未简化布尔代数中相同函数的两种不同符号。

mi是要映射的最小项(即,在真值表中输出为 1 的行)。

mi是要映射的最大项(即,真值表中输出为 0 的行)

在上面的例子中,四个输入变量可以用 16 种不同的方式组合,所以真值表有 16 行,卡诺图有 16 个位置。因此,卡诺图以 4 × 4 的网格排列。
行和列索引(显示在卡诺图的顶部和左侧)以格雷码而不是二进制数字顺序排列。格雷码确保每对相邻单元之间只有一个变量发生变化。完整卡诺图的每个单元格都包含一个二进制数字,表示该输入组合的函数输出。
分组
在构建卡诺图之后,它被用来寻找布尔代数最简单的可能形式之一——规范形式——获取真值表中的信息。卡诺图中相邻的 1 代表简化表达式的机会。最终表达式的最小项是通过在地图中圈出 1 组来找到的。Minterm 组必须是矩形的,并且面积必须是 2 的幂(即 1、2、4、8...)。最小项矩形应尽可能大,不包含任何 0。组可以重叠以使每个组更大。下例中的最优分组用绿、红、蓝线标记,红、绿组重叠。红色组是一个 2×2 的正方形,绿色组是一个 4×1 的矩形,重叠区域用棕色表示。

单元格通常由描述单元格覆盖的输入的逻辑值的简写表示。例如,AD表示一个单元格覆盖了A和D为1的 2x2 区域,即上图中编号为 13、9、15、11 的单元格。另一方面,A D(非)表示A为真且D为假(即D(非)为真)的单元格。
网格是环形连接的,这意味着矩形组可以环绕边缘(见图)。最右边的单元格实际上与最左边的单元格“相邻”,因为相应的输入值仅相差一位;同样,最顶端的和最底端的也是如此。因此,A D(非)可以是一个有效术语——它在顶部包括单元格 12 和 8,并环绕到底部以包括单元格 10 和 14——就像B(非) D(非)一样,它包括四个角。
解决方案
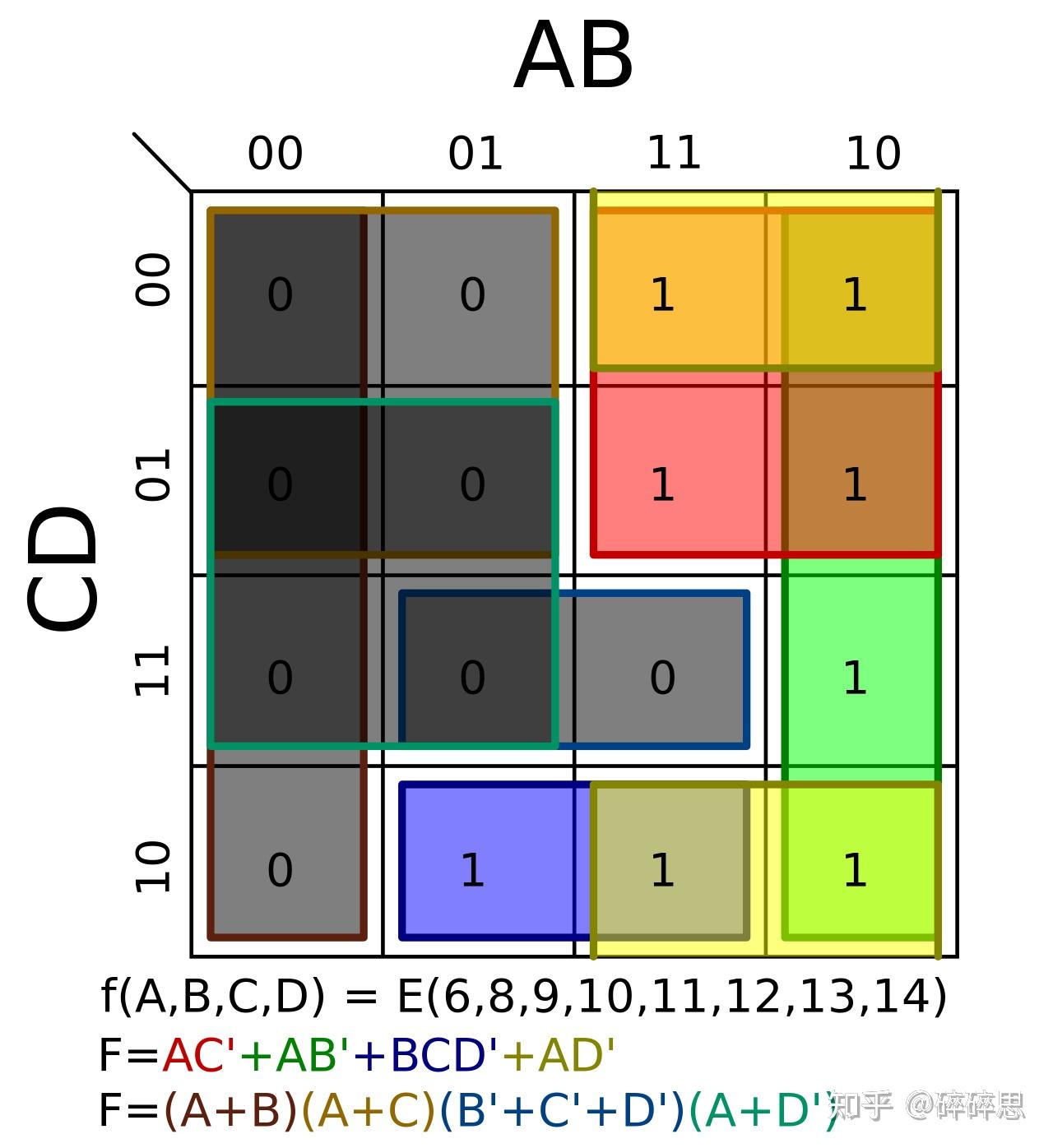
函数 f(A, B, C, D) 的 K-map 显示为对应于最小项的彩色矩形。棕色区域是红色 2×2 正方形和绿色 4×1 矩形的重叠部分。f 的倒数的 K-map 显示为灰色矩形,对应于 maxterms。

一旦构建了卡诺图并且相邻的 1 通过矩形和方形框连接起来,就可以通过检查每个框内哪些变量保持相同来找到代数小项。
对于红色分组:
- A是相同的,并且在整个框中都等于 1,因此它应该包含在红色最小项的代数表示中。
- B不保持相同的状态(它从 1 变为 0),因此应该被排除在外。
- C不变。它始终为 0,因此应包括其补码 NOT-C。因此,应包括C。
- D发生变化,因此被排除在外。
因此,布尔乘积和表达式中的第一个最小项是A C(非)。
对于绿色分组,A和B保持相同的状态,而C和D改变。B为 0,必须先取反才能包含在内。因此,第二项是A B(非)。请注意,绿色分组与红色分组重叠是可以接受的。
同样,蓝色分组给出了术语BC D((非))。
将每一组的解组合起来:电路的最后的化简结果如下:
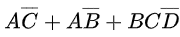
还有其他方式,就不展开描述了,可以自行学习。
Problem 72-Kmap1
题目说明
根据卡诺图来实现电路:
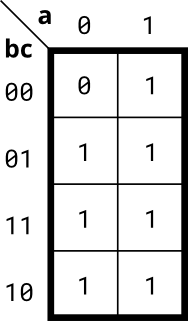
图片来自HDLBits
我们可以尝试最大项之积和最小项之和的形式来完成电路设计。
模块端口声明
module top_module(
input a,
input b,
input c,
output out );
题目解析
按照下图方框化简:
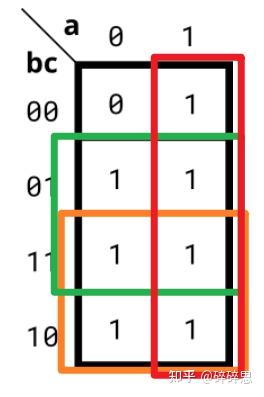
得到:
f(a,b,c)=a+b+c=a'b'c'(摩根定理)
所以可以有两种方式解决。
module top_module(
input logic a,
input logic b,
input logic c,
output logic out
assign out = a | b | c;
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中的Ref是参考波形,Yours是你的代码生成的波形,网站会对比这两个波形,一旦这两者不匹配,仿真结果会变红。
这一题就结束了。
Problem 73-Kmap2
题目说明
还是根据卡诺图来设计电路,本题为4个变量。
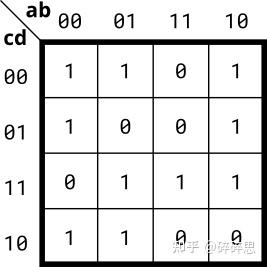
图片来自HDLBits
在编写verilog之前,我们可先化简卡诺图。
模块端口声明
module top_module(
input a, b, cin,
output cout, sum );
题目解析
根据下图先化简卡诺图得到最小和:
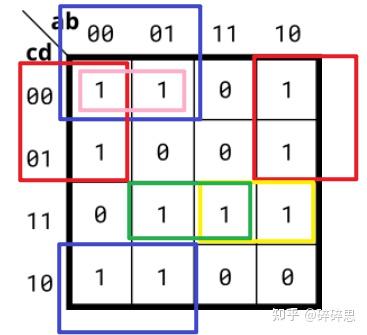
f(a,b,c,d) = a'd'+b'c'+ab'd+bcd
module top_module(
input logic a,
input logic b,
input logic c,
input logic d,
output logic out
assign out = ~a&~d | ~b&~c | a&~b&d | b&c&d ;
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中的Ref是参考波形,Yours是你的代码生成的波形,网站会对比这两个波形,一旦这两者不匹配,仿真结果会变红。
这一题就结束了。
Problem 74-Kmap3
题目说明
根据卡诺图实现电路:
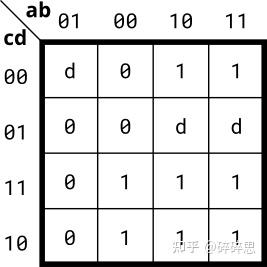
图片来自HDLBits
还是先化简卡诺图,其中D为don't care值。相当于X。可以一起圈。
模块端口声明
module top_module(
input a,
input b,
input c,
input d,
output out );
题目解析
可以这样圈,进行化简:
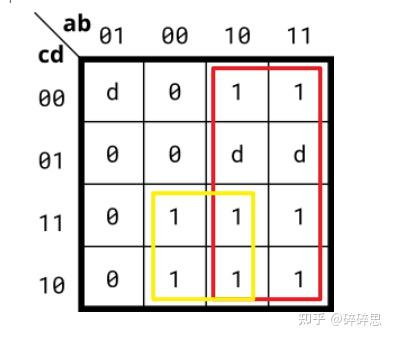
PS:
2^n个方格相邻的最小项,可以合并成1项,消去n个变量。
module top_module(
input logic a,
input logic b,
input logic c,
input logic d,
output logic out );
assign out = a | ~b&c ;
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中的Ref是参考波形,Yours是你的代码生成的波形,网站会对比这两个波形,一旦这两者不匹配,仿真结果会变红。
这一题就结束了。
Problem 75-Kmap4
题目说明
根据卡诺图实现电路:
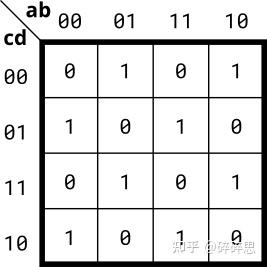
图片来自HDLBits
模块端口声明
module top_module(
input a,
input b,
input c,
input d,
output out );
题目解析
这题没什么能化简的,就老老实实敲代码吧。
module top_module(
input logic a,
input logic b,
input logic c,
input logic d,
output logic out
assign out = ~a&b&~c&~d | a&~b&~c&~d | ~a&~b&~c&d | a&b&~c&d
| ~a&b&c&d | a&~b&c&d | ~a&~b&c&~d | a&b&c&~d ;
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中的Ref是参考波形,Yours是你的代码生成的波形,网站会对比这两个波形,一旦这两者不匹配,仿真结果会变红。
这一题就结束了。
Problem 76-ece241_2013_q2
题目说明
一个4输入a, b, c, d和一输出的逻辑电路,当输入为2, 7或15时,输出为1, 当输入为0, 1, 4, 5, 6, 9, 10, 13, 或 14 时,输出为0,当输入为3,8,11或12时输出为任意值。举例来说,7对应输入abcd为0,1,1,1.
注意: 该电路的SOP和POS必须均为化简后的最小值
模块端口声明
module top_module (
input a,
input b,
input c,
input d,
output out_sop,
output out_pos
题目解析
直接根据题目做出答案比较难,所以我们需要先根据题目画出卡诺图:

SOP圈法就是圈1,如下:

POS圈法就是圈0,如下:

module top_module (
input logic a,
input logic b,
input logic c,
input logic d,
output logic out_sop,
output logic out_pos
assign out_sop = c&d | ~a&~b&c ;
assign out_pos = c&(~a|b)&(~b|~c|d) ;
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中无波形。
这一题就结束了。
Problem 77-m2014 q3
题目说明
还是根据卡诺图实现电路:
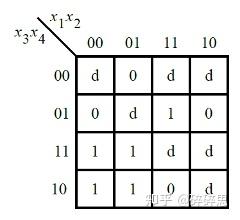
图片来自HDLBits
模块端口声明
module top_module (
input [4:1] x,
output f );
题目解析
没什么难度,与其他没区别。
module top_module (
input logic [4:1] x,
output logic f );
assign f = (~x[1] & x[3]) | (x[1] & x[2] & ~x[3]);
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中无波形。
这一题就结束了。
Problem 78-2012_q1g
题目说明
还是根据卡诺图画出电路:
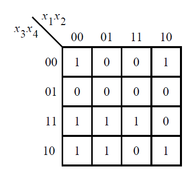
图片来自HDLBits
模块端口声明
module top_module (
input [4:1] x,
output f
题目解析
都是同一个道理。
module top_module (
input logic [4:1] x,
output logic f
assign f = ~x[2]&~x[4] | ~x[1]&x[3] | x[2]&x[3]&x[4] ;
endmodule

点击Submit,等待一会就能看到下图结果:

注意图中无波形。
这一题就结束了。
Problem 79-ece241_2014_q3
题目说明
根据题目给出的卡诺图,用一个4-1的多路选择器和尽可能多的2-1多路选择器来实现电路,不允许使用其他逻辑门,必须使用ab作为选择器的输入。
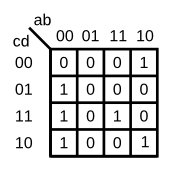
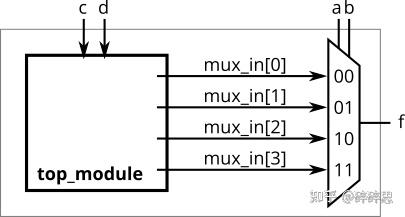
图片来自HDLBits
模块端口声明
module top_module (
input c,
input d,
output [3:0] mux_in
题目解析
开始题目比较“萌”,因为把东西结合起来了,所以一时难以下手。

这题如果从选择器入手就比较简单了,从图中看到,当ab为固定值,输出是由cd的输入决定。
接下来就是看卡诺图了,从卡诺图中:
- 当ab == 2'b00时,化简卡诺图,得到mux_in[0] = c+d=cd;
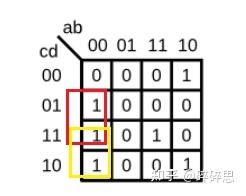
-
当ab == 2'b01时,化简卡诺图,得到mux_in[1] = 1'b0;
-
当ab == 2'b10时,化简卡诺图,得到mux_in[2] = d';
-
当ab == 2'b11时,化简卡诺图,得到mux_in[3] = cd;
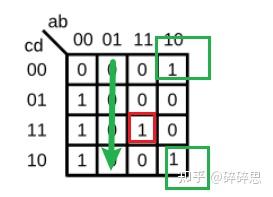
此处需注意mux_in[3:0], 一个高位低位的问题,不要搞反了。
module top_module (
input logic c,
input logic d,
output logic [3:0] mux_in
